吉林省长春市朝阳区2024-2025学年八年级上学期10月期中考试数学试卷

这是一份吉林省长春市朝阳区2024-2025学年八年级上学期10月期中考试数学试卷，共11页。试卷主要包含了5124， 下列运算正确的是， 下列命题是真命题的是等内容，欢迎下载使用。

本试卷包括三道大题，共24小题，共6页. 全卷满分120分. 考试时间为90分钟.
注意事项：
1. 答题前，考生务必将自己的姓名、准考证号填写在答题卡上，并将条形码准确粘贴在条形码区域内.
2. 答题时，考生务必按照考试要求在答题卡上的指定区域内作答，在草稿纸、试卷上答题无效.
一、选择题 (每小题3分，共24分)
1. 在实数0、 2、 137 、0.5124中, 无理数是
A. 0 B. 2 C. 137 D. 0.5124
2. 如果 x²=9,那么x的值为
A. 3 B. -3 C. ±3 D.±3
3. 下列运算正确的是
A. 2a·a=3a B.a²⋅a⁴=a⁸ C.a³²=a⁵ D.ab³=a³b³
4. 下列命题是真命题的是
A. 无理数都是无限小数 B. 带根号的数都是无理数
C. 无理数可以转化成分数 D. 数轴上的点与有理数一一对应
5. 已知 n<15A. 2 B. 3 C. 4 D. 5
6. 如图，有一池塘，要测池塘两端A、B的距离，可先在平地上取一个可以直接到达A和B的点C, 连结AC 并延长到D, 使CD=CA. 连结BC 并延长到E, 使CE=CB. 连结DE, 那么DE的长就是A、B的距离. 解决这个问题依据的数学道理是
A. 两边及其夹角分别相等的两个三角形全等
B. 两角及其夹边分别相等的两个三角形全等
C. 两角分别相等且其中一组等角的对边相等的两个三角形全等
D. 三边分别相等的两个三角形全等
7. 如图，现有三种不同尺寸的卡片，分别是正方形卡片A、正方形卡片B和长方形卡片C. 若要拼成一个长为a+2b、宽为a+b的大长方形，则需要卡片 C的张数为
A, 1 B. 2 C. 3 D. 4
8. 已知(x -1)x+1=x²-1,x-1x²+x+1=x³-1,x-1x³+x²+x+1=x⁴-1,x-1x⁴+x³+x²+x+1=x⁵-1,··根据以上等式的规律，可以推算出 22024+22023+⋯+22+2的值为
A.2²⁰²⁵-1 B.2²⁰²⁵+1 C.2²⁰²⁵+2 D.2²⁰²⁵-2
二、填空题 (每小题3分，共18分)
9. 多项式 4x³-6x²+2x的公因式是 .
10. 举反例说明命题“若x<1，则x<0”是假命题时，可举的反例是： x=. (写出一个即可)
11. 若多项式 x²-6x+m是某一个多项式的平方，则常数项m的值为 .
12. 若x+2y-3=0,则2x-2·4y的值为 .
13. 若 a=2⁵⁰,b=3⁴⁰,c=4³⁰,则 a、b、c 的大小关系是 . (用“<”连接)
14. 如图, AB=AC, AD=AE, BD=CE, 且点B、D、E在同一条直线上. 给出下面四个结论;
①△ABD≌△ACE;
②∠ADE=∠CAE+∠ACE;
③AD∥CE;
④∠BEC=∠DAE.
上述结论中，正确结论的序号有 .
三、解答题 (本大题10 小题，共78分)
15. (6分) 计算:
1-12+16+3-27. 2y¹²÷-2y²³.
16. (6分) 把下列多项式分解因式：
1a²-2a+1. 22a²-8b².
17. (6分) 先化简, 再求值:( 3+x-3+x-xx-2,, 其中x=-1.
18. (7分) 已知某正数的两个平方根分别为4a+5和1-2a.
(1) 求这个正数.
(2) 求 a²-1的立方根.
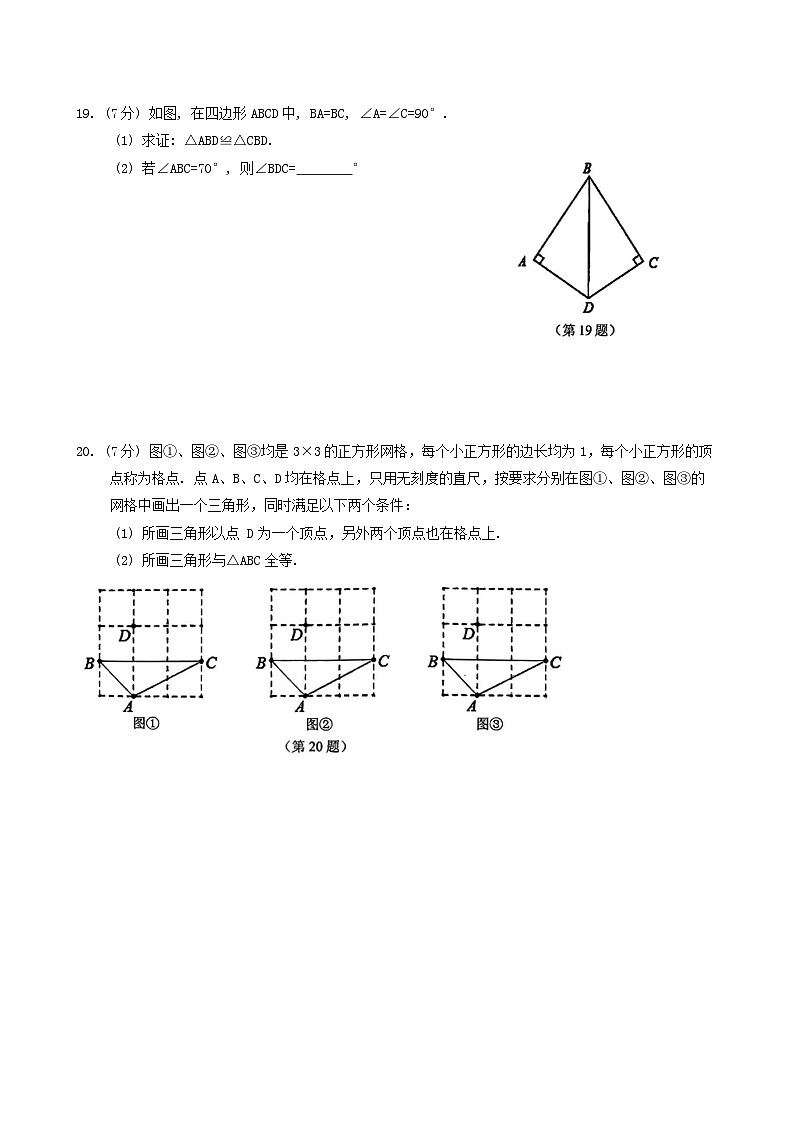
19. (7分) 如图, 在四边形ABCD中, BA=BC, ∠A=∠C=90°.
(1) 求证: △ABD≌△CBD.
(2) 若∠ABC=70°, 则∠BDC= °
20. (7分) 图①、图②、图③均是3×3的正方形网格，每个小正方形的边长均为1，每个小正方形的顶点称为格点. 点A、B、C、D均在格点上，只用无刻度的直尺，按要求分别在图①、图②、图③的网格中画出一个三角形，同时满足以下两个条件：
(1) 所画三角形以点 D为一个顶点，另外两个顶点也在格点上.
(2) 所画三角形与△ABC全等.
21. (8分) 如图, 点A、D、C、B在同一条直线上, DE∥CF, DF∥EC, AD=BC.
(1) 求证: △DEC≌△CFD.
(2) 求证: AE∥FB.
22. (9分)
【问题探究】小聪遇到一个数学问题: 如图①, 在△ABC中, AB=6, AC=4, AD是BC边上的中线，求AD的取值范围.
他的做法是: 延长 AD至点 E, 使DE=AD, 连结BE, 证明△BED≌△CAD,再经过推理和计算解决了问题.
请回答：
(1) 小聪证明△BED≌△CAD 的判定定理是 .
A. S. A. S. B. A. S. A. C. A. A. S. D. S. S. S.
(2) AD 的取值范围是 .
【方法运用】
(3)如图②,在△ABC中, AD是BC边上的中线,过点B作BM⊥AD交AD的延长线于点M,过点 C作CN⊥AD 于点 N, 求证: △BMD≌△CND.
(4)如图③,点P是△ABC中线AD上一点,连结BP、CP.若∠BPD=∠CAD,AC=4, PC=3, 则PD的取值范围是 .
23. (10分)在数学中，通常可以运用一些公式来解决问题. 比如，运用两数和的完全平方公式 a+b²=a²+2ab+b²,能够在三个代数式 a+b、ab、a²+b²中，当已知其中任意两个代数式的值时，求出第三个代数式的值. 例如：已知 a+b=3,ab=2,求 a²+b²的值.
解：将a+b=3 两边同时平方, 得 a+b²=3²,
即 a²+2ab+b²=9,
因为 ab=2,
等量代换，得 a²+b²+2×2=9,
所以 a²+b²=5.
请根据以上信息，解答下列问题.
(1) 已知 a-b=1,a²+b²=17, 求 ab的值.
(2) 如图，已知两个正方形的边长分别为a、b，若 a+b=7,ab=9,，求图中阴影部分的面积.
(3) 若 2025-xx-2024=-6,则 2025-x²+x-2024²的值为 .
24. (12分)如图, 四边形ABCD 的各内角均为直角, AB=CD=12,AD=BC=6,点M、N分别是AB、BC中点. 动点P 从点A 出发, 沿折线AD—DC向终点C运动, 过点P作 PH⊥AB于点 H, 连结PM、MN. 设点P运动时间为t秒t0).
(1) 当点 P运动到AD中点时, 求证: △PAM≅△NBM.
(2) 若点P以每秒2个单位长度的速度运动，
① 如图①, 当点 P 在边 AD上时, PH=. (用含t的代数式表示)
② 如图②，当点P在边DC上时(点P不与点D重合) ，易知 PH=DA,DP=AH,若 HM=4,求t的值.
(3) 若点P以每秒x个单位长度的速度运动，当 t=3时，恰好 △PHM与 △NBM全等，直接写出所有满足条件的x的值.
2024—2025学年度 (上学期) 期中质量检测·八年级数学
参考答案
一、选择题(每小题3分，共24分)
1. B 2. C 3. D 4. A 5. B 6. A 7 . C 8 D
二、填空题(每小题3分，共18分)
9. 2x 10 12 (答案不唯一，满足0≤x<1即可) 11 9
12. 2 13. a三、解答题 (本大题10 小题，共78分)
15. 计算:
解： 1-12+16+3-27
= -1+4-3
= 0 (3分)
2y¹²÷-2y²³
=y¹²÷-8y⁶
-18y6 (6分)
评分说明：(1)、(2)结果正确，且过程正确，得3分； 结果正确，但过程不正确或没有过程，不得分；结果不正确，但过程正确，得2分.
16. 把下列多项式分解因式：
解： 1a²-2a+1
=a-1² (3分)
22a²-8b²
=2a²-4b²
= 2(a+2b)(a-2b) (6分)
评分说明：(2)结果正确，且过程正确或没有过程，均得3分； 结果不正确，但答对 2a²-4b²得2分17. 解: (3+x)(-3+x)-x(x-2)
=x²-9-x²-2x (2分)
=x²-9-x²+2x
=2x-9. (4分)
当x=-1时, 原式=2×(-1)-9=-11. (6分)
18. 解:
(1) 根据题意, 得4a+5+1-2a=0 , (2分)
解得a=-3, (3分)
4a+5=4×(-3)+5=-7,
这个正数是( -72⋯49. (4分)
(2) ∵a=-3,
∴a²-1=-3²-1=8, (5分)
∴38=2. (7分)
19. (1) 证明: ∵∠A=∠C=90°, (1分)
∴△ABD与△CBD 都是直角三角形.
在 Rt△ABD 与 Rt△CBD中, (2分)
∵BA=BC, (3分)
BD=BD, (4分)
∴Rt△ABD≌Rt△CBD (H. L.). (5分)
(2) 解: 55 °. (7分)
20. 解: 如图所示:
评分说明：画出图①、 图②、 图③、 图④中任意三个即可. 画正确一个图，得3分； 画正确两个图，得5分，画正确三个图，得7分.
21. 解:
(1) 证明: ∵DE∥CF,
∴∠EDC=∠FCD.
∵DF∥EC,
∴∠ECD=∠FDC. (1分)
在△EDC与△FCD中,
∵∠EDC=∠FCD,
DC=CD, (2分)
∠ECD=∠FDC,
∴△DEC≌△CFD (A. S. A.). (3分)
(2) 方法1:
证明: 由(1) 知△DEC≌△CFD,
∴DE=CF. (4分)
∵点A、D、C、B在同一条直线上, ∠EDC=∠FCD,
∴∠ADE+∠EDC=180°, ∠BCF+∠FCD=180°,
∴∠ADE=∠BCF. (5分)
在△EDC与△FCD中,
∵DE=CF,
∠ADE=∠BCF,
AD=BC, (6分)
∴△ADE≌△BCF (S. A. S.), (7分)
∴∠A=∠B,
∴AE∥FB (8分)
方法2：
证明: 由(1) 知△DEC≌△CFD,
∴CE:DF. (4分)
∵点 A、D、C、B在同一条直线上, AD=BC,
∴AD+DC=BC+CD,
∴AC=BD. (5分)
在△ACE与△BDF中,
∵CE=DF,
∠ACE=∠BDF, (6分)
AC=BD,
∴△ACE≌△BDF(SA. S), (7分)
∴∠A=∠B,
∴AE∥FB. (8分)
22. 解:
【问题探究】
(1) A . (2分)
(2) 1【方法运用】
(3) 证明: ∵AD是BC边上的中线,
∴BD=CD.
∵BM⊥AD, CN⊥AD,
∴∠BMD=∠CND=90°,
在△BDM与△CDN中,
∵∠BMD=∠CND,
∠BDM=∠CDN,
BD=CD,
∴△BMD≌△CND (A A. S.). (7分)
(4) 1223. 解: (1) 将a-b=1 两边同时平方, 得( a-b²=1²,
即 a²-2ab+b²=1, (2分)
因为 a²+b²=17,
等量代换, 得17-2ab=1,
所以 ab=8. (3分)
(2) 图中阴影部分的面积 =a2-2×12ba-b=a2+b2-ab. (5分)
根据题意，得( a+b²=7²,
即 a²+2ab+b²=49,
∵ab=9,
∴a²+b²+2×9=49,
a²+b²=31.
图中阴影部分的面积=31-9=22. (8分)
(3) 13 . (10分)
24. 解:(1) 证明: ∵点P是AD中点, 点N是BC中点,
∴AP=12AD,BN=12BC,
又∵AD=BC,
∴AP=BN.
∵点M是AB中点,
∴AM=BM.
在△PAM 与△NBM中,
∵AP=BN,
∠PAM=∠NBM,
AM=BM,
∴△PAM≌△NBM(S. A. S.). (4分)
(2) ① PH= 2t . (6分)
② 当点P在边DC上时, DP=2t-6.
HM=AM-AH=12AB-DP=4, 即 12×12-2t-6=4,解得t=4.
HM=AH-AM=DP-12AB=4, 即 2t-6-12×12=4,解得t=8. (9分)
(3) 1, 3, 5. (12分)