浙江省杭州市西湖区绿城育华中学2023—2024学年上学期期中考试八年级数学试卷

这是一份浙江省杭州市西湖区绿城育华中学2023—2024学年上学期期中考试八年级数学试卷，共25页。试卷主要包含了选择题等内容，欢迎下载使用。

1．（3分）2023年9月23日至10月8日第19届亚运会在杭州圆满闭幕．在这16天里，来自亚洲45个国家和地区的1万多名运动员参加了本届亚运会．中国体育代表团获得201枚金牌、383枚奖牌，取得亚运会参赛历史最好成绩．在“杭”“州”“亚”“运”四个字中，是轴对称图形的是
A．杭B．州C．亚D．运
2．（3分）若，则下列式子中错误的是
A．B．C．D．
3．（3分）下面各组线段中，能组成三角形的是
A．5，11，6B．8，8，16C．10，5，4D．6，9，14
4．（3分）画△中边上的高，下列四个画法中正确的是
A．B．
C．D．
5．（3分）下列选项中，可以作为命题“一个钝角与一个锐角的差是锐角”的反例是
A．，B．，C．，D．，
6．（3分）若等腰三角形的两边长分别为3和6，则它的周长是
A．12或15B．15C．12D．14
7．（3分）我国古代数学著作《九章算术》中有这样一个问题：今有池方一丈，葭生其中央，出水一尺．引葭赴岸，适于岸齐，问水深、葭长各几何？”这道题的意思是：“有一个边长为10尺的正方形水池，在水池的正中央（底面中点）长着一根芦苇，芦苇露出水面1尺．若将芦苇拉到水池一边，芦苇的顶端恰好到达池边的水面，问水的深度与这根芦苇的长度分别是多少？”该题所求的水深为
A．9尺B．10尺C．12尺D．13尺
8．（3分）如图，，．，，垂足分别是点、，，，则的长是
A．B．2C．D．
9．（3分）如图，把纸片的沿折叠，点落在四边形外，则、与的关系是
A．B．C．D．
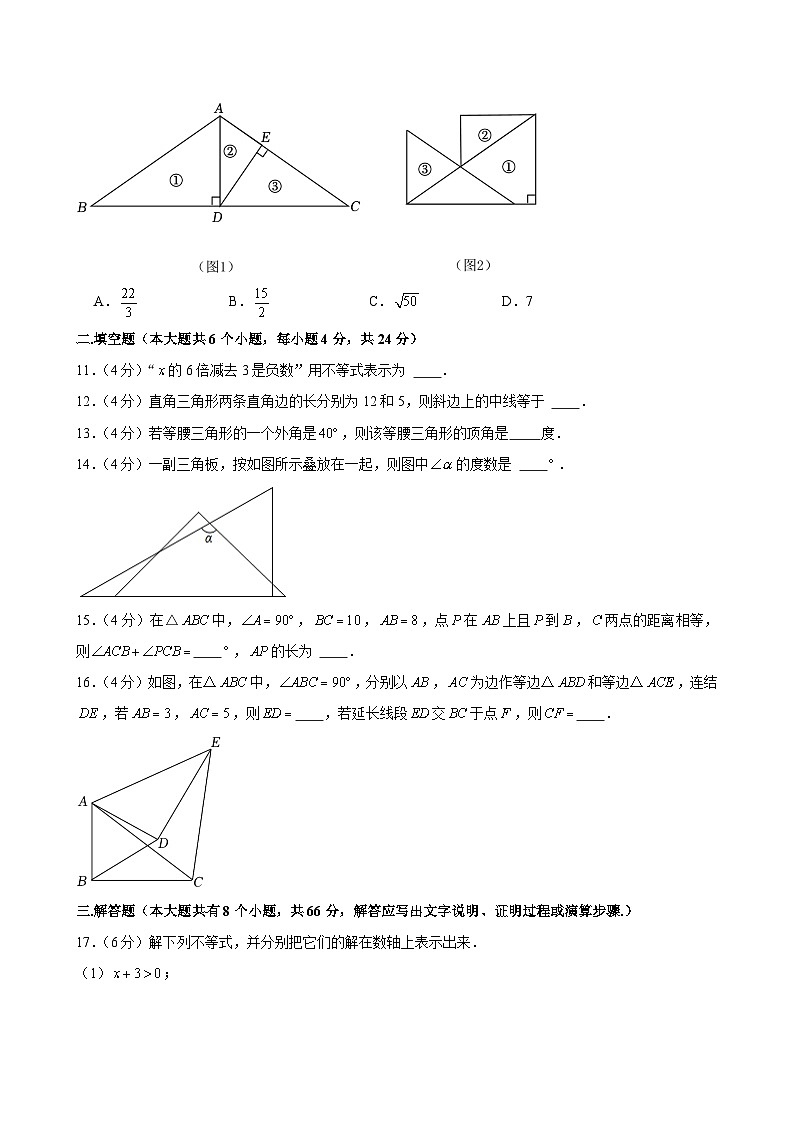
10．（3分）将一个等腰三角形纸板沿垂线段，进行剪切，得到三角形①②③，再按如图2方式拼放，其中与共线．若，则的长为
A．B．C．D．7
二.填空题（本大题共6个小题，每小题4分，共24分）
11．（4分）“的6倍减去3是负数”用不等式表示为 ．
12．（4分）直角三角形两条直角边的长分别为12和5，则斜边上的中线等于 ．
13．（4分）若等腰三角形的一个外角是，则该等腰三角形的顶角是 度．
14．（4分）一副三角板，按如图所示叠放在一起，则图中的度数是 ．
15．（4分）在△中，，，，点在上且到，两点的距离相等，则 ，的长为 ．
16．（4分）如图，在△中，，分别以，为边作等边△和等边△，连结，若，，则 ，若延长线段交于点，则 ．
三.解答题（本大题共有8个小题，共66分，解答应写出文字说明、证明过程或演算步骤.）
17．（6分）解下列不等式，并分别把它们的解在数轴上表示出来．
（1）；
（2）．
18．（6分）如图，已知射线，，，若．
（1）求的度数；
（2）求的度数．
19．（6分）有一电脑程序：设按一次按键，屏幕上的数字就会自动加上2．已知屏幕上的初始数字为，按次按键后：
（1）若屏幕上显示的数字为18，求的值；
（2）若屏幕上显示的数字不小于100，求的取值范围．
20．（8分）如图，在△和△中，，，与相交于点．求证：
（1）△△；
（2）．
21．（8分）风筝起源于中国，最早的风筝是由古代哲学家墨翟制造的．方方同学做了一个如图所示的风筝骨架，其中，，与相交于点．
（1）请在下列两组判断中选择一组说明理由：
第一组判断：垂直平分；
第二组判断：平分．
（2）设厘米，厘米，厘米，用一张轻薄的棉纸覆盖风筝骨架，至少需要多少平方厘米的棉纸？
22．（10分）如图，在中，，点、、分别在、、边上，且，．
（1）求证：是等腰三角形．
（2）若为等边三角形，求的度数．
23．（10分）如果三角形有一边上的中线恰好等于这边的长，那么我们称这个三角形为“美丽三角形”．
（1）如图中，，，求证是美丽三角形；
（2）是一个美丽三角形，并且，，求的长．
24．（12分）如图，在△中，，，点是射线上的动点，连接，点关于直线的对称点为点，射线与射线交于点，连接．
（1）如图1，是线段上的点．
①若，求的度数．
②若，则 （直接写出度数）．
（2）如图2，点是线段延长线上的点，其余条件不变，连接．
①在图2中，用三角板与刻度尺依题意补全图形；
②若，求证：△△．
2023-2024学年浙江省杭州市上城区绿城育华中学八年级（上）期中数学试卷
参考答案与试题解析
一、选择题（本大题共有10个小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的）
1．（3分）2023年9月23日至10月8日第19届亚运会在杭州圆满闭幕．在这16天里，来自亚洲45个国家和地区的1万多名运动员参加了本届亚运会．中国体育代表团获得201枚金牌、383枚奖牌，取得亚运会参赛历史最好成绩．在“杭”“州”“亚”“运”四个字中，是轴对称图形的是
A．杭B．州C．亚D．运
【分析】根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．
【解答】解：，，选项中的字都不能找到一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形；
选项中的字能找到一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形．
故选：．
【点评】本题考查了轴对称图形的概念，熟知轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合是解题的关键．
2．（3分）若，则下列式子中错误的是
A．B．C．D．
【分析】根据不等式的性质解答．
【解答】解：、在不等式的两边同时加上3，不等号的方向不变，即，原变形正确，故此选项不符合题意．
、在不等式的两边同时减去3，不等号的方向不变，即，原变形正确，故此选项不符合题意．
、在不等式的两边同时乘以，不等号的方向改变，即，原变形错误，故此选项符合题意．
、在不等式的两边同时除以3，不等号的方向不变，即，原变形正确，故此选项不符合题意．
故选：．
【点评】本题主要考查了不等式的性质，在不等式两边同乘以（或除以）同一个数时，不仅要考虑这个数不等于0，而且必须先确定这个数是正数还是负数，如果是负数，不等号的方向必须改变．
3．（3分）下面各组线段中，能组成三角形的是
A．5，11，6B．8，8，16C．10，5，4D．6，9，14
【分析】根据三角形的任意两边之和大于第三边对各选项分析判断后利用排除法求解．
【解答】解：、，不能组成三角形，故选项错误；
、，不能组成三角形，故选项错误；
、，不能组成三角形，故选项错误；
、，能组成三角形，故选项正确．
故选：．
【点评】本题考查了三角形的三边关系，是基础题，熟记三边关系是解题的关键．
4．（3分）画△中边上的高，下列四个画法中正确的是
A．B．
C．D．
【分析】根据三角形的高线的定义：过三角形的一个顶点向对边引垂线，顶点与垂足之间的距离叫做三角形的高对各选项图形判断即可．
【解答】解：由三角形的高线的定义，选项图形表示△中边上的高．
故选：．
【点评】本题考查了三角形的角平分线、中线和高，熟记定义并准确识图是解题的关键．
5．（3分）下列选项中，可以作为命题“一个钝角与一个锐角的差是锐角”的反例是
A．，B．，C．，D．，
【分析】找到满足“一个钝角与一个锐角的差是直角或钝角”的一组即可．
【解答】解：，而又不是锐角，
选项符合题意，
故选：．
【点评】考查了命题与定理的知识，解题的关键是了解举出反例可以说明一个命题是假命题，难度不大．
6．（3分）若等腰三角形的两边长分别为3和6，则它的周长是
A．12或15B．15C．12D．14
【分析】由三角形三边关系定理判定等腰三角形的腰长是6，即可求出等腰三角形的周长．
【解答】解：如果等腰三角形的腰长是3，
，不满足三角形三边关系，
等腰三角形的腰长不可能是3；
如果等腰三角形的腰长是6，
，满足三角形三边关系定理，
等腰三角形的腰长是6，
等腰三角形的周长．
故选：．
【点评】本题考查等腰三角形的性质，三角形三边关系，关键是由三角形三边关系定理判定等腰三角形的腰长是6．
7．（3分）我国古代数学著作《九章算术》中有这样一个问题：今有池方一丈，葭生其中央，出水一尺．引葭赴岸，适于岸齐，问水深、葭长各几何？”这道题的意思是：“有一个边长为10尺的正方形水池，在水池的正中央（底面中点）长着一根芦苇，芦苇露出水面1尺．若将芦苇拉到水池一边，芦苇的顶端恰好到达池边的水面，问水的深度与这根芦苇的长度分别是多少？”该题所求的水深为
A．9尺B．10尺C．12尺D．13尺
【分析】设水深为尺，根据勾股定理解答．
【解答】解：设水深尺，芦苇尺，
由勾股定理：，
解得：，，
水深12尺，
故选：．
【点评】本题考查勾股定理的应用．熟练掌握勾股定理是解题的关键．
8．（3分）如图，，．，，垂足分别是点、，，，则的长是
A．B．2C．D．
【分析】根据条件可以得出，进而得出，就可以得出，就可以求出的值．
【解答】解：，，
，
．
，
．
在和中，
，
，
，．
故选：．
【点评】本题考查全等三角形的判定和性质、熟练掌握全等三角形的判定和性质是解决问题的关键，学会正确寻找全等三角形，属于中考常考题型．
9．（3分）如图，把纸片的沿折叠，点落在四边形外，则、与的关系是
A．B．C．D．
【分析】如图，分别延长交于点，然后利用三角形的外角与内角的关系可以得到，，而根据折叠可以得到，，然后利用等式的性质即可求解．
【解答】解：如图：分别延长、交于点，
，，
而根据折叠可以得到，，
．
故选：．
【点评】本题考查图形的折叠与拼接，同时考查了三角形、四边形等几何基本知识，解题时应分别对每一个图形进行仔细分析，难度不大．
10．（3分）将一个等腰三角形纸板沿垂线段，进行剪切，得到三角形①②③，再按如图2方式拼放，其中与共线．若，则的长为
A．B．C．D．7
【分析】设为，为，为，图2中的余角为，根据题意和图形可得，设为，则，根据上式列出方程即可解答．
【解答】解：如图，设为，为，为，图2中的余角为，
为等腰三角形，，
，，
，
，
结合两图，可得，
设为，
根据勾股定理得，
，
解得：，
，
故选：．
【点评】本题考查了等腰三角形的性质，勾股定理，结合两图得到等量关系式是解题关键．
二.填空题（本大题共6个小题，每小题4分，共24分）
11．（4分）“的6倍减去3是负数”用不等式表示为 ．
【分析】根据题意建立关于的不等式即可．
【解答】解：由题知，
“的6倍减去3”可表示为：．
因为“的6倍减去3是负数”，
所以．
故答案为：．
【点评】本题主要考查了由实际问题抽象出一元一次不等式，能根据题意正确表示出“的6倍减去3”是解题的关键．
12．（4分）直角三角形两条直角边的长分别为12和5，则斜边上的中线等于 6.5 ．
【分析】利用勾股定理求得直角三角形的斜边，然后利用直角三角形斜边上的中线等于斜边的一半解题．
【解答】解：如图，在中，，，，
则根据勾股定理知，，
为斜边上的中线，
．
故答案为：6.5．
【点评】本题考查了勾股定理、直角三角形斜边上的中线．勾股定理：如果直角三角形两直角边分别为，，斜边为，那么．即直角三角形，两直角边的平方和等于斜边的平方．直角三角形的性质：在直角三角形中斜边上的中线等于斜边的一半．
13．（4分）若等腰三角形的一个外角是，则该等腰三角形的顶角是 140 度．
【分析】根据邻补角的定义求出与外角相邻的内角，再根据等腰三角形的性质解答．
【解答】解：等腰三角形的一个外角是，
与这个外角相邻的内角为，
该等腰三角形的顶角是140度．
故答案为：140．
【点评】本题考查了等腰三角形的性质，邻补角的定义，是基础题，等腰三角形的钝角只能是顶角．
14．（4分）一副三角板，按如图所示叠放在一起，则图中的度数是 105 ．
【分析】如图，由三角形内角和定理，得，可推断出．
【解答】解：如图．
由题意得：，．
，
．
故答案为：．
【点评】本题主要考查三角形内角和定理，熟练掌握三角形内角和定理是解决本题的关键．
15．（4分）在△中，，，，点在上且到，两点的距离相等，则 90 ，的长为 ．
【分析】根据勾股定理求出，由点在上，且到，两点的距离相等，得，所以，然后利用勾股定理即可解决问题．
【解答】解：如图，在△中，，
，
，，
，
点在上，且到，两点的距离相等，
，
，
，
在△中，，根据勾股定理得：
，
，
．
故答案为：，．
【点评】本题考查了勾股定理，线段垂直平分线的性质，解决本题的关键是掌握勾股定理．
16．（4分）如图，在△中，，分别以，为边作等边△和等边△，连结，若，，则 4 ，若延长线段交于点，则 ．
【分析】连接，利用等边三角形的性质和已知条件证明△△即可得出，再运用勾股定理求得即可求得；可证得△△，得出，，设，则，再运用勾股定理建立方程求得，即可求得．
【解答】解：如图，连接，
分别以，为边作等边△和等边△，
，，，
，
即，
在△和△中，
，
△△，
，，
在△中，，，，
，
；
，
，
在△和△中，
，
△△，
，
，
设，则，
，
，
整理得：，
，
，
，
，
故答案为：4，．
【点评】本题考查了等边三角形的性质、直角三角形的性质，全等三角形的判定和性质，勾股定理等，解题的关键是掌握全等三角形的判定和性质．
三.解答题（本大题共有8个小题，共66分，解答应写出文字说明、证明过程或演算步骤.）
17．（6分）解下列不等式，并分别把它们的解在数轴上表示出来．
（1）；
（2）．
【分析】（1）移项即可求得；
（2）去分母、移项、合并同类项即可求解．
【解答】解：（1），
移项得：；
在数轴上表示解集为：
；
（2），
去分母得：，
移项得：，
合并同类项得：，
在数轴上表示解集为：
．
【点评】此题主要考查了一元一次不等式的解法，正确掌握基本解题方法是解题关键．
18．（6分）如图，已知射线，，，若．
（1）求的度数；
（2）求的度数．
【分析】（1）由邻补角互补，即可求出的度数．
（2）由等腰三角形的性质推出，，由三角形外角的性质得到，即可求出．
【解答】解：（1），，
；
（2），
，，
，
，
，
．
【点评】本题考查等腰三角形的性质，三角形外角的性质，关键是由以上知识点推出．
19．（6分）有一电脑程序：设按一次按键，屏幕上的数字就会自动加上2．已知屏幕上的初始数字为，按次按键后：
（1）若屏幕上显示的数字为18，求的值；
（2）若屏幕上显示的数字不小于100，求的取值范围．
【分析】（1）根据“按次按键后，屏幕上显示的数字为18”，列出一元一次方程，解方程即可；
（2）根据“按次按键后，屏幕上显示的数字不小于100”，列出一元一次不等式，解一元一次不等式即可．
【解答】解：（1）由题意得：，
解得：；
（2）由题意得：，
解得：．
【点评】本题考查了一元一次不等式组的应用以及一元一次方程的应用，解题的关键是：（1）找准等量关系，正确列出一元一次方程；（2）根据各数量之间的关系，正确列出一元一次不等式组．
20．（8分）如图，在△和△中，，，与相交于点．求证：
（1）△△；
（2）．
【分析】（1）利用即可证得结论；
（2）根据全等三角形性质可得：，，再利用角的关系即可证得结论．
【解答】（1）证明：在和△△中，，
，
△△；
（2）证明：由（1）知△△，
，，
，
即．
【点评】此题主要考查全等三角形的判定和性质，关键是学生对直角三角形全等的判定和全等三角形的性质的理解和掌握．
21．（8分）风筝起源于中国，最早的风筝是由古代哲学家墨翟制造的．方方同学做了一个如图所示的风筝骨架，其中，，与相交于点．
（1）请在下列两组判断中选择一组说明理由：
第一组判断：垂直平分；
第二组判断：平分．
（2）设厘米，厘米，厘米，用一张轻薄的棉纸覆盖风筝骨架，至少需要多少平方厘米的棉纸？
【分析】（1）证垂直平分即可；（2）解：先得，再得△的面积（平方厘米），即可得四边形的面积（平方厘米）．
【解答】（1）证明：，，
，都在的垂直平分线上，
垂直平分；
，
平分．
（2）解：由厘米，厘米，厘米，
得，
得，
得△的面积（平方厘米），
得四边形的面积（平方厘米），
答：至少需要1200平方厘米的棉纸．
【点评】本题主要考查了垂直平分线和勾股定理，解题关键是正确计算．
22．（10分）如图，在中，，点、、分别在、、边上，且，．
（1）求证：是等腰三角形．
（2）若为等边三角形，求的度数．
【分析】（1）由，，，．利用边角边定理证明，然后即可求证是等腰三角形．
（2）得出．可得．则．可求出结论．
【解答】（1）证明：，
．
在和中，
．
．
是等腰三角形．
（2）解：为等边三角形，
．
，
．
，
．
．
．
【点评】本题考查了全等三角形的判定和性质，等腰三角形的性质，等边三角形的性质，熟练掌握全等三角形的判定和性质是解题的关键．
23．（10分）如果三角形有一边上的中线恰好等于这边的长，那么我们称这个三角形为“美丽三角形”．
（1）如图中，，，求证是美丽三角形；
（2）是一个美丽三角形，并且，，求的长．
【分析】（1）过点作于，根据等腰三角形的性质求出，根据勾股定理求出，根据“美丽三角形”的定义证明；
（2）分边上的中线等于，边上的中线等于两种情况，根据勾股定理计算．
【解答】（1）证明：过点作于，
，，
，
由勾股定理得，，
，即是“美丽三角形”；
（2）解：当边上的中线等于时，如图2，
，
当边上的中线等于时，
，即，
解得，，
综上所述，或．
【点评】本题考查的是勾股定理，如果直角三角形的两条直角边长分别是，，斜边长为，那么．
24．（12分）如图，在△中，，，点是射线上的动点，连接，点关于直线的对称点为点，射线与射线交于点，连接．
（1）如图1，是线段上的点．
①若，求的度数．
②若，则 45 （直接写出度数）．
（2）如图2，点是线段延长线上的点，其余条件不变，连接．
①在图2中，用三角板与刻度尺依题意补全图形；
②若，求证：△△．
【分析】（1）①根据题意，先求出，再由判定△为等边三角形即可；
②先求出，再依据△为等腰三角形两底角相等求出，最后由求出的度数．
（2）①过点用三角板先作的垂线，然后用刻度尺量取，再连接相关端点补充图形即可；
②先利用外角的性质和等量代换求出，进而得到，然后通过等腰直角三角形及轴对称的性质得出，最后由证明△△即可．
【解答】（1）解：①根据轴对称的性质，，，
又，
，，
△为等边三角形．
．
故的度数为．
②，，
．
，，
．
故答案为：．
（2）①解：连接，过点用三角板作的垂线，交于点，在该垂线上用刻度尺截取，连接交射线于点，如图所示．
②证明：，，
，
．
在等腰△中，，
，，
．
对于等腰直角△，，则．
．
又，
．
．
在△和△中，，，，
△△．
【点评】本题考查了等腰直角三角形的性质，轴对称图形的性质，三角形全等的判定等．本题的关键是从△为等腰三角形破题，然后利用等腰△的性质，推导相关结论．