广东省佛山市南海区平洲第二初级中学2024-2025学年七年级上学期10月月考数学试题

这是一份广东省佛山市南海区平洲第二初级中学2024-2025学年七年级上学期10月月考数学试题，共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共有10个小题，每小题3分，共30分．）
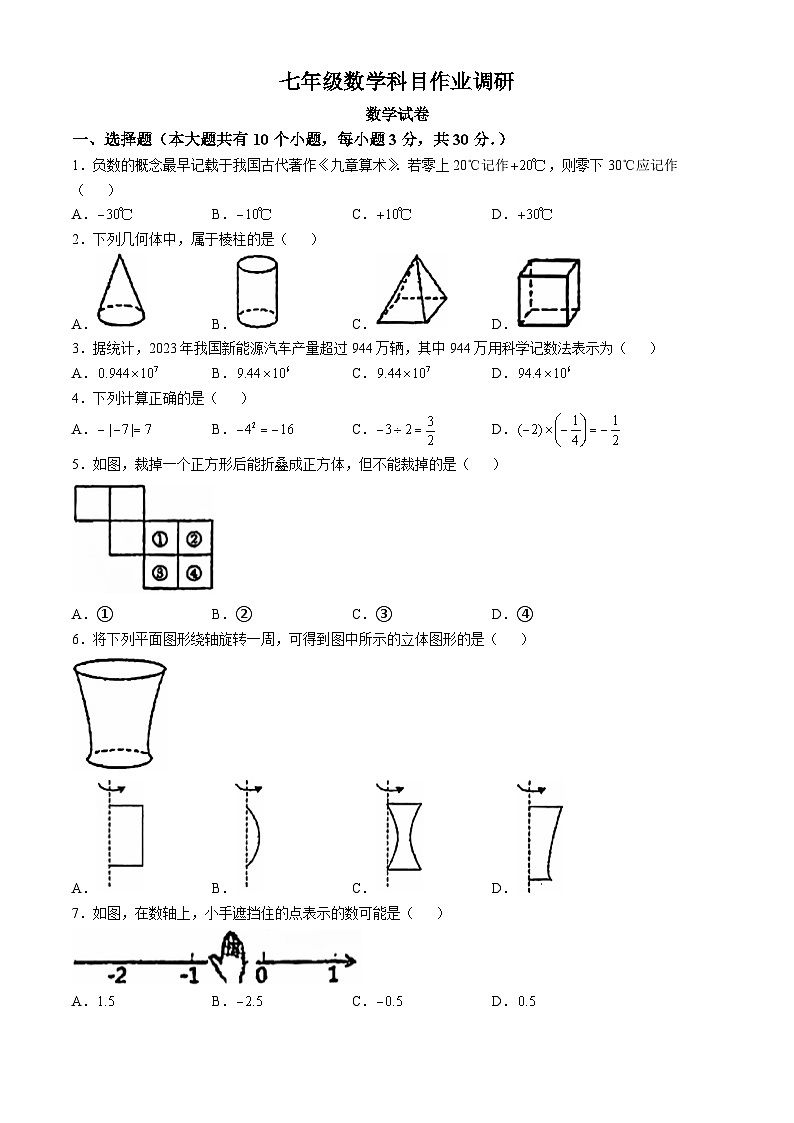
1．负数的概念最早记载于我国古代著作《九章算术》．若零上20℃记作，则零下30℃应记作（ ）
A．B．C．D．
2．下列几何体中，属于棱柱的是（ ）
A．B．C．D．
3．据统计，2023年我国新能源汽车产量超过944万辆，其中944万用科学记数法表示为（ ）
A．B．C．D．
4．下列计算正确的是（ ）
A．B．C．D．
5．如图，裁掉一个正方形后能折叠成正方体，但不能裁掉的是（ ）
A．①B．②C．③D．④
6．将下列平面图形绕轴旋转一周，可得到图中所示的立体图形的是（ ）
A．B．C．D．
7．如图，在数轴上，小手遮挡住的点表示的数可能是（ ）
A．B．C．D．
8．由若干个相同的小正方体搭成的一个几何体的主视图和左视图如图所示，则组成这个几何体的小正方体的个数最少有（ ）个．
A．3B．4C．5D．6
9．如图是正方体展开图，将《论语》十二章中的一句话：“学而不思则罔”．这六个字写在正方体展开图的六个面内，则“而”对面的文字是（ ）
A．不B．思C．则D．罔
10．已知整数，，，，…，满足下列条件：，，，，…，以此类推，则的值为（ ）
A．B．C．D．
二、填空题（本大题共5小题，每小题3分，共15分）
11．计算：________．
12．一个几何体的表面能够展开成如图所示的平面图形，则这个几何体的名称是________．
13．冬季里沛县某一天的最低气温是，最高气温是5℃，这一天的温差为________．
14．单项式的系数是________．
15．《九章算术》是中国古代第一部数学专著，不仅最早提到分数问题，也首先记录了盈不足等问题，在第七章“盈不足”中有这样一个问题：“今有蒲生一日，长三尺；蒲生日自半”．其意思是“有蒲这种植物，蒲第一日长了3尺，以后蒲每日长的长度是前一日的一半”．请计算出第三日后，蒲的长度为________尺．
三、解答题（一）（本大题共3小题，每小题7分，共21分）
16．计算：．
17．已知下列各数：，，，．
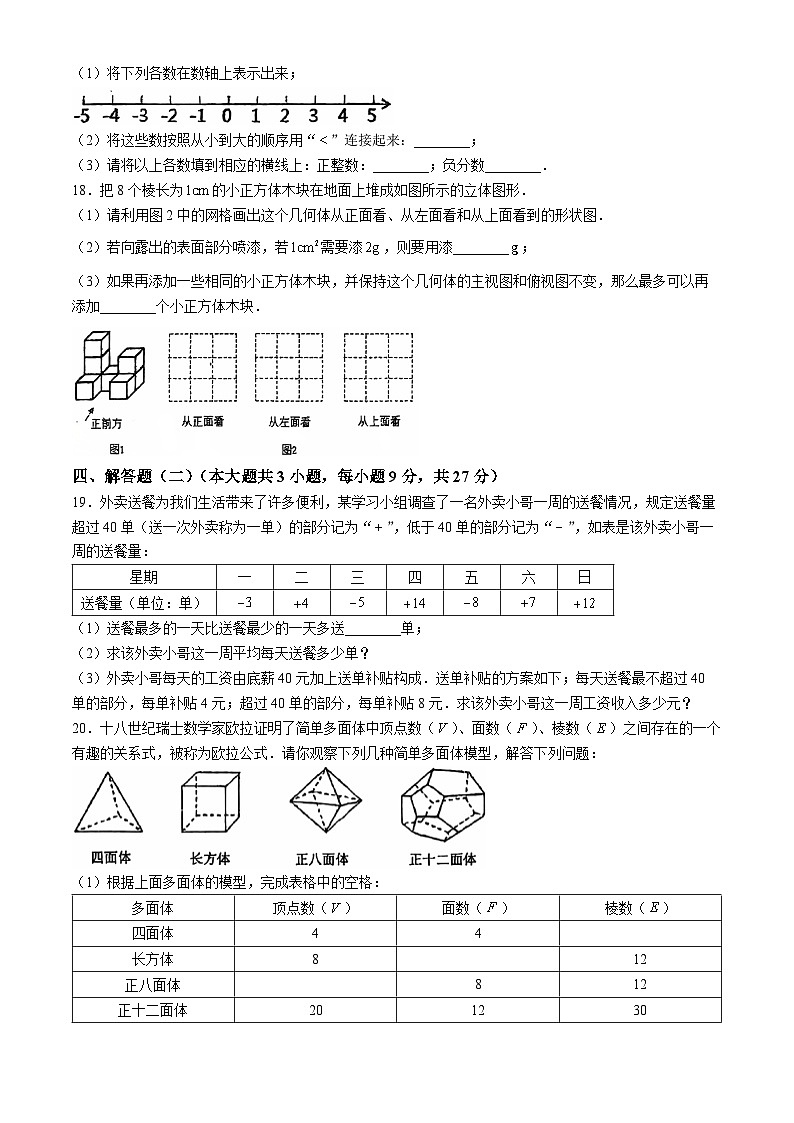
（1）将下列各数在数轴上表示出来；
（2）将这些数按照从小到大的顺序用“”连接起来：________；
（3）请将以上各数填到相应的横线上：正整数：________；负分数________．
18．把8个棱长为的小正方体木块在地面上堆成如图所示的立体图形．
（1）请利用图2中的网格画出这个几何体从正面看、从左面看和从上面看到的形状图．
（2）若向露出的表面部分喷漆，若需要漆，则要用漆________；
（3）如果再添加一些相同的小正方体木块，并保持这个几何体的主视图和俯视图不变，那么最多可以再添加________个小正方体木块．
四、解答题（二）（本大题共3小题，每小题9分，共27分）
19．外卖送餐为我们生活带来了许多便利，某学习小组调查了一名外卖小哥一周的送餐情况，规定送餐量超过40单（送一次外卖称为一单）的部分记为“”，低于40单的部分记为“”，如表是该外卖小哥一周的送餐量：
（1）送餐最多的一天比送餐最少的一天多送________单；
（2）求该外卖小哥这一周平均每天送餐多少单？
（3）外卖小哥每天的工资由底薪40元加上送单补贴构成．送单补贴的方案如下；每天送餐最不超过40单的部分，每单补贴4元；超过40单的部分，每单补贴8元．求该外卖小哥这一周工资收入多少元？
20．十八世纪瑞士数学家欧拉证明了简单多面体中顶点数（）、面数（）、棱数（）之间存在的一个有趣的关系式，被称为欧拉公式．请你观察下列几种简单多面体模型，解答下列问题：
（1）根据上面多面体的模型，完成表格中的空格：
（2）你发现顶点数（）、面数（）、棱数（）之间存在的关系式是________；
（3）一个多面体的面数比顶点数大8，棱数为30，则这个多面体的面数是多少？
21．综合与实践：用一张正方形的纸片制作一个无盖长方形盒子．
如果我们按照如图所示的方式，将正方形的四个角剪掉四个大小相同的小正方形，然后沿虚线折起来，就可以做成一个无盖的长方体盒子．
（1）如果原正方形纸片的边长为，剪去的正方形的边长为，请你用含，的代数式来表示这个无盖长方体纸盒的容积________．
（2）如果，剪去的小正方形的边长按整数值依次变化，即分别取，，，，，，，，，时，折成的无盖长方体的容积分别是多少？请你将计算的结果填入如表：
（3）观察绘制的统计表，你发现，随着剪去的小正方形的边长的增大，所折无盖长方体盒子的容积如何变化？（ ）
A．一直增大B．一直减小C．先增大后减小D．先减小后增大
（4）为了得到边长为的无盖长方体盒子的最大容积，小明请教学习编程的哥哥后得到；当剪去小正方形的边长为原正方形纸片边长的时，此时容积最大，请你求出此时无盖长方体的最大容积：________．
五、解答题（三）（本大题共2小题，第22题13分，第23题14分，共27分）
22．我们知道，可以理解为，它表示：数轴上表示数的点到原点的距离，这是绝对值的几何意义．进一步地，数轴上的两个点，，分别用数，表示，那么，两点之间的距离为，反过来，式子的几何意义是：数轴上表示数的点和表示数的点之间的距离．利用此结论，回答以下问题：
（1）数轴上表示数的点和表示数3的点之间的距离是________；
（2）数轴上点用数表示，若，那么的值为________；
（3）数轴上点用数表示，探究以下几个问题：
①若，那么的值是________；
②满足整数有________个；
③有最小值，最小值是：________；
④求的最小值．
23．如图，数轴上、两点所对应的数分别是和，且．
（1）则________，________，、两点之间的距离________；
（2）有一动点从点出发第一次向左运动1个单位长度，然后在新的位置第二次运动，向右运动2个单位长度，在此位置第三次运动，向左运动3个单位长度，在此位置第四次运动，向右运动4个单位长度…按照如此规律不断地左右运动，当运动到2023次时，求点所对应的有理数．
（3）在（2）的条件下，点在某次运动时恰好到达某一个位置，使点到点的距离是点到点的距离的2倍？请求出此时点的位置，并直接写出是第几次运动．
七年级数学科目作业调研
数学答案
一、选择题（本大题共有10个小题，每小题3分，共30分．）
1．A 2．C 3．B 4．B 5．A 6．D 7．C 8．A 9．C 10．C
二、填空题（本大题共5小题，每小题3分，共15分）
11．2024 12．圆柱 13．15℃ 14． 15．
三、解答题（一）（本大题共3小题，每小题7分，共21分）
16．
17．（1）
（2）
（3），
18．（1）
（2）58 （3）3
19．（1）22
（2）（单）
（单）
（单）
答：该外卖小哥这一周平均每天送餐43单．
（3）
（元）
答：该外卖小哥这一周工资收入1632元．
20．（1）6，6，6
（2）；
（3），∴，
∴
∴，∴．
21．（1）；
（2）588，576；
（3）C；
（4）．
22．（1）8；
（2）；
（3）①8或；②6；③2025；
④∵的中间一项是，
∴当时，原式必有最小值；
∴原式
．
∴最小值为1023132．
23．（1），7，12；
（2）略．（3）略．星期
一
二
三
四
五
六
日
送餐量（单位：单）
多面体
顶点数（）
面数（）
棱数（）
四面体
4
4
长方体
8
12
正八面体
8
12
正十二面体
20
12
30
剪去正方形的边长/
1
2
3
4
5
6
7
8
9
10
容积/
324
512
500
384
252
128
36
0