期浙江省金华市2024年数学九上开学质量检测模拟试题【含答案】

这是一份期浙江省金华市2024年数学九上开学质量检测模拟试题【含答案】，共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
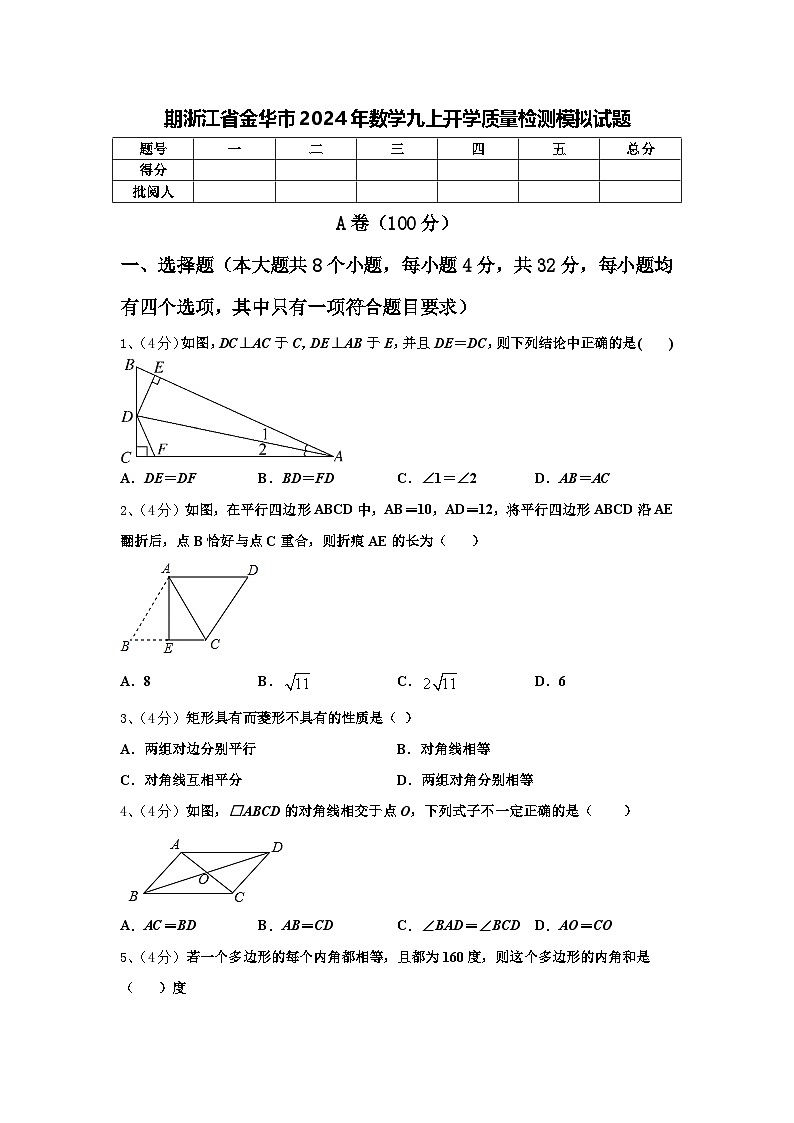
1、（4分）如图，DC⊥AC于C，DE⊥AB于E，并且DE＝DC，则下列结论中正确的是( )
A．DE＝DFB．BD＝FDC．∠1＝∠2D．AB＝AC
2、（4分）如图，在平行四边形ABCD中，AB＝10，AD＝12，将平行四边形ABCD沿AE翻折后，点B恰好与点C重合，则折痕AE的长为（ ）
A．8B．C．D．6
3、（4分）矩形具有而菱形不具有的性质是（ ）
A．两组对边分别平行B．对角线相等
C．对角线互相平分D．两组对角分别相等
4、（4分）如图，□ABCD的对角线相交于点O，下列式子不一定正确的是（ ）
A．AC＝BDB．AB＝CDC．∠BAD＝∠BCDD．AO＝CO
5、（4分）若一个多边形的每个内角都相等，且都为160度，则这个多边形的内角和是（ ）度
A．2520B．2880C．3060D．3240
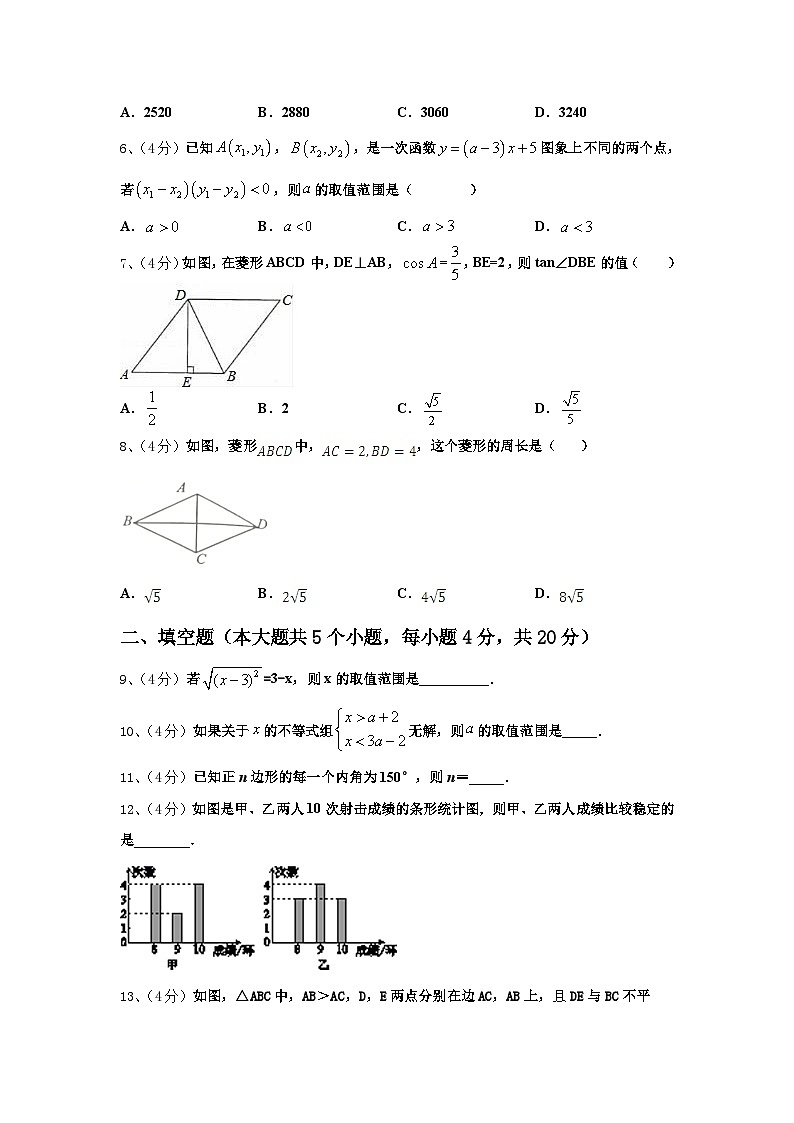
6、（4分）已知，，是一次函数图象上不同的两个点，若，则的取值范围是（ ）
A．B．C．D．
7、（4分）如图，在菱形ABCD中，DE⊥AB，=，BE=2，则tan∠DBE的值（ ）
A．B．2C．D．
8、（4分）如图，菱形中，，这个菱形的周长是（ ）
A．B．C．D．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）若=3-x，则x的取值范围是__________．
10、（4分）如果关于的不等式组无解，则的取值范围是_____．
11、（4分）已知正n边形的每一个内角为150°，则n＝_____．
12、（4分）如图是甲、乙两人10次射击成绩的条形统计图，则甲、乙两人成绩比较稳定的是________．
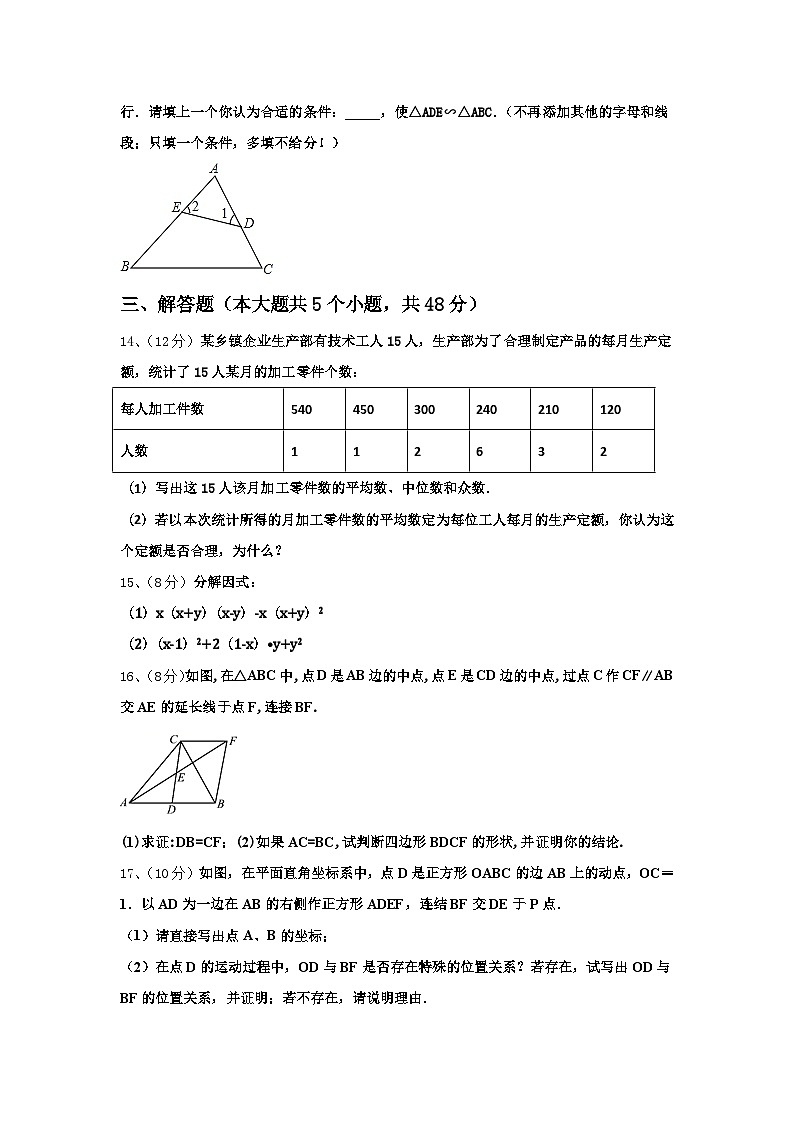
13、（4分）如图，△ABC中，AB＞AC，D，E两点分别在边AC，AB上，且DE与BC不平行．请填上一个你认为合适的条件：_____，使△ADE∽△ABC．（不再添加其他的字母和线段；只填一个条件，多填不给分！）
三、解答题（本大题共5个小题，共48分）
14、（12分）某乡镇企业生产部有技术工人15人，生产部为了合理制定产品的每月生产定额，统计了15人某月的加工零件个数：
（1）写出这15人该月加工零件数的平均数、中位数和众数．
（2）若以本次统计所得的月加工零件数的平均数定为每位工人每月的生产定额，你认为这个定额是否合理，为什么？
15、（8分）分解因式：
（1）x（x+y）（x-y）-x（x+y）2
（2）（x-1）2+2（1-x）•y+y2
16、（8分）如图,在△ABC中,点D是AB边的中点,点E是CD边的中点,过点C作CF∥AB交AE的延长线于点F,连接BF.
(1)求证:DB=CF；(2)如果AC=BC,试判断四边形BDCF的形状,并证明你的结论.
17、（10分）如图，在平面直角坐标系中，点D是正方形OABC的边AB上的动点，OC＝1．以AD为一边在AB的右侧作正方形ADEF，连结BF交DE于P点．
（1）请直接写出点A、B的坐标；
（2）在点D的运动过程中，OD与BF是否存在特殊的位置关系？若存在，试写出OD与BF的位置关系，并证明；若不存在，请说明理由．
（3）当P点为线段DE的三等分点时，试求出AF的长度．
18、（10分） “一路一带”倡议6岁了！到日前为止，中国已与126个国家和29个国际组织签署174份合作文件，共建“一路一带”国家已由亚欧延伸至非洲、拉美、南太等区域.截止2019年一季度末，人民币海外基金业务规模约3000亿元，其投资范围覆盖交通运输、电力能源、金融业和制造业等重要行业，投资行业统计图如图所示．
（1）求投资制造业的基金约为多少亿元？
（2）按照规划，中国将继续对“一路一带”基金增加投入，到2019年三季度末，共增加投入630亿元，假设平均每季度的增长率相等，求平均每季度的增长率是多少？
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）正五边形的内角和等于______度．
20、（4分）菱形的两条对角线长分别为10cm和24cm，则该菱形的面积是_________；
21、（4分）已知直线y=2x+4与x轴、y轴分别交于A、B两点，点P（-1，m）为平面直角坐标系内一动点，若△ABP面积为1，则m的值为______．
22、（4分）一组数据﹣1，0，1，2，3的方差是_____．
23、（4分）如图，在Rt△ABC中，∠BAC＝90°，AB＝8，AC＝6，DE是AB边的垂直平分线，垂足为D，交边BC于点E，连接AE，则△ACE的周长为________．

二、解答题（本大题共3个小题，共30分）
24、（8分）如图，在平面直角坐标系中，已知点A（﹣1，3），B（﹣3，1），C（﹣1，1）．且△A1B1C1与△ABC关于原点O成中心对称．
（1）画出△A1B1C1，并写出A1的坐标；
（1）P（a，b）是△ABC的边AC上一点，△ABC经平移后点P的对应点P′（a+3，b+1），请画出平移后的△A1B1C1．
25、（10分）某市开展“环境治理留住青山绿水，绿色发展赢得金山银山”活动，对其周边的环境污染进行综合治理．年对、两区的空气量进行监测，将当月每天的空气污染指数（简称：）的平均值作为每个月的空气污染指数，并将年空气污染指数绘制如下表．据了解，空气污染指数时，空气质量为优：空气污染指数时，空气质量为良：空气污染指数时，空气质量为轻微污染．
（1）请求出、两区的空气污染指数的平均数；
（2）请从平均数、众数、中位数、方差等统计量中选两个对区、区的空气质量进行有效对比，说明哪一个地区的环境状况较好．
26、（12分）先化简，然后a在﹣1、1、2三个数中任选一个合适的数代入求值．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、C
【解析】
分析：如图，由已知条件判断AD平分∠BAC即可解决问题．
详解：如图，∵DC⊥AC于C，DE⊥AB于E，且DE=DC，∴点D在∠BAC的角平分线上，∴∠1=∠1．
故选C．

点睛：该题主要考查了角平分线的判定及其性质的应用问题；牢固掌握角平分线的性质是解题的关键．
2、A
【解析】
由点B恰好与点C重合，可知AE垂直平分BC，根据勾股定理计算AE的长即可．
【详解】
解：∵翻折后点B恰好与点C重合，
∴AE⊥BC，BE=CE，
∵BC=AD=12，
∴BE=6，
∴AE=，
故选：A．
本题主要考查了平行四边形的性质，作图-轴对称变换，掌握平行四边形的性质，作图-轴对称变换是解题的关键.
3、B
【解析】
根据矩形与菱形的性质对各选项解析判断后利用排除法求解：
A．矩形与菱形的两组对边都分别平行，故本选项错误；
B．矩形的对角线相等，菱形的对角线不相等，故本选项正确；
C．矩形与菱形的对角线都互相平分，故本选项错误；
D．矩形与菱形的两组对角都分别相等，故本选项错误．
故选B．
4、A
【解析】
根据平行四边形的性质逐项判断即可得．
【详解】
A、平行四边形的对角线不一定相等，则不一定正确，此项符合题意
B、平行四边形的两组对边分别相等，则一定正确，此项不符题意
C、平行四边形的两组对角分别相等，则一定正确，此项不符题意
D、平行四边形的两对角线互相平分，则一定正确，此项不符题意
故选：A．
本题考查了平行四边形的性质，熟记平行四边形的性质是解题关键．
5、B
【解析】
n边形的内角和是(n－2)180°，由此列方程求解.
【详解】
设这个多边形的边数为n，
则(n－2)180°＝160°n，
解得，n＝18.
则(n－2)180°＝(18－2)×180°＝2880°.
故选B.
本题主要考查了多边形的内角和，n边形的内角和是(n－2)180°.
6、D
【解析】
根据可得出与异号，进而得出，解之即可得出结论.
【详解】
，
与异号，
，解得：.
故选：.
本题考查了一次函数的性质，熟练掌握“当时，随的增大而减小”是解题的关键.
7、B
【解析】
试题解析：
设AE=3x，
∵

∴BE=5x−3x=2x=2，
∴x=1,
∴AD=5,AE=3,


故选B.
8、C
【解析】
通过菱形性质及勾股定理求出边AB的值，周长为4AB即可．
【详解】
解：因为四边形ABCD是菱形，
所以AC⊥BD，设AC与BD交于点O，
则AO=1，BO=2，
所以AB=．
周长为4AB=4．
故选：C．
本题主要考查了菱形的性质，解决四边形问题一般转化为三角形问题．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、
【解析】
试题解析：∵=3﹣x，
∴x-3≤0，
解得：x≤3，
10、a≤1．
【解析】
分别求解两个不等式,当不等式“大大小小”时不等式组无解,
【详解】
解：
∴不等式组的解集是
∵不等式组无解,即,
解得：
本题考查了求不等式组的解集和不等式组无解的情况,属于简单题,熟悉无解的含义是解题关键.
11、1
【解析】
试题解析：由题意可得：
解得
故多边形是1边形．
故答案为1．
12、乙
【解析】
∵通过观察条形统计图可知：乙的成绩更整齐，也相对更稳定，
∴甲的方差大于乙的方差，
∴乙的成绩比较稳定.
故答案为乙．
点睛：本题考查方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．
13、∠B=∠1或
【解析】
此题答案不唯一，注意此题的已知条件是：∠A=∠A，可以根据有两角对应相等的三角形相似或有两边对应成比例且夹角相等三角形相似，添加条件即可.
【详解】
此题答案不唯一，如∠B=∠1或．
∵∠B=∠1，∠A=∠A，
∴△ADE∽△ABC；
∵，∠A=∠A，
∴△ADE∽△ABC；
故答案为∠B=∠1或
此题考查了相似三角形的判定：有两角对应相等的三角形相似；有两边对应成比例且夹角相等三角形相似，要注意正确找出两三角形的对应边、对应角，根据判定定理解题.
三、解答题（本大题共5个小题，共48分）
14、（1）平均数：260件；中位数：240件；众数：240件（2）不合理，定额为240较为合理
【解析】
分析：(1)平均数=加工零件总数÷总人数,中位数是将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.本题中应是第7个数.众数又是指一组数据中出现次数最多的数据.240出现6次.
(2)应根据中位数和众数综合考虑.
详解：（1）平均数： ；中位数：240件；众数：240件．
（2）不合理，因为表中数据显示，每月能完成260件的人数一共是4人，还有11人不能达到此定额，尽管260是平均数，但不利于调动多数员工的积极性，因为240既是中位数，又是众数，是大多数人能达到的定额，故定额为240较为合理．
点睛：本题考查了平均数、中位数和众数的知识，在求本题的平均数时,应注意先算出15个人加工的零件总数.为了大多数人能达到的定额,制定标准零件总数时一般应采用中位数或众数.
15、（1）-2xy（x+y）；（2）（x-1-y）2
【解析】
（1）提公因式x（x+y），合并即可；
（2）利用完全平方式进行分解.
【详解】
（1）原式=x（x+y）[（x-y）-（x+y）]
=-2xy（x+y）
（2）原式=（x-1）2-2（x-1）y+y2
=（x-1-y）2
本题考查的知识点是提取公因式法因式分解和完全平方式，解题关键是求出多项式里各项的公因式，提公因式．
16、 (1)证明见解析；（2）四边形BDCF是矩形，理由见解析.
【解析】
(1)证明：∵CF∥AB，
∴∠DAE＝∠CFE．又∵DE＝CE，∠AED＝∠FEC，
∴△ADE≌△FCE，∴AD＝CF．∵AD＝DB，∴DB＝CF．
(2)四边形BDCF是矩形．
证明：由(1)知DB＝CF，又DB∥CF，
∴四边形BDCF为平行四边形．
∵AC＝BC，AD＝DB，∴CD⊥AB．
∴四边形BDCF是矩形．
17、（1）A（1，0），B（1，1）；（2）OD⊥BF，理由见解析；（3）当P点为线段DE的三等分点时，AF的长度为2或2．
【解析】
（1）利用正方形的性质得出OA=AB=1，即可得出结论；
（2）利用SAS判断出△AOD≌△BAF，进而得出∠AOD=∠BAF，即可得出结论；
（3）先表示出BD，DP，再判断出△BDP∽△BAF，得出，代入解方程即可得出结论。
【详解】
（1）∵四边形OABC是正方形，
∴BC⊥OC，AB⊥OA，OB＝AB＝BC＝OC，
∵OC＝1，
∴BC＝AB＝1，
∴A（1，0），B（1，1）；
（2）OD⊥BF，理由：如图，延长OD交BF于G，
∵四边形ADEF是正方形，
∴AD＝AF，∠BAF＝∠OAD，
在△AOD和△BAF中， ，
∴△AOD≌△BAF（SAS），
∴∠AOD＝∠BAF，
∴∠BAF+∠AFB＝90°，
∴∠AOD+AFB＝90°，
∴∠OGF＝90°，
∴OD⊥BF；
（3）设正方形ADEF的边长为x，
∴AF＝AD＝DE＝x，
∴BD＝AB﹣AD＝1﹣x，
∵点P是DE的三等分点，
∴DP＝AF＝x或DP＝AF＝x
∵DE∥AF，
∴△BDP∽△BAF，
∴，
∴或 ，
∴x＝2或x＝2，
当P点为线段DE的三等分点时，AF的长度为2或2．
本题是四边形综合题，主要考查了正方形的性质，全等三角形的判定和性质，垂直的判定，相似三角形的判定和性质，用方程的思想解决问题是解本题的
18、（1）630亿元；（2）10%
【解析】
（1）由投资电力能源所在扇形的圆心角求出投资电力能源所占比例，再利用投资制造业的基金=投资总金额×D所占的比例，即可求出结论；
（2）设平均每季度的增长率是x，根据2019年一季度末及三季度末的投资总额，即可得出关于x的一元二次方程，解之取其正值即可得出结论．
【详解】
（1）×100%=20%，3000×（1-12%-15%-20%-32%）=630（亿元）．
（2）设平均每季度的增长率是x，依题意，得：
3000（1+x）2=3000+630，
解得：x1=0.1=10%，x2=-2.1（舍去）．
答：平均每季度增长10%．
考查了一元二次方程的应用以及用样本估计总体，解题的关键是：（1）求出图中B所占比例；（2）找准等量关系，正确列出一元二次方程．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、540
【解析】
过正五边形五个顶点，可以画三条对角线，把五边形分成3个三角形
∴正五边形的内角和=3180=540°
20、110cm1．
【解析】
试题解析：S=×10×14=110cm1．
考点：菱形的性质．
21、3或1
【解析】
过点P作PE⊥x轴，交线段AB于点E，即可求点E坐标，根据题意可求点A，点B坐标，由可求m的值．
【详解】
解：∵直线y=2x+4与x轴、y轴分别交于A、B两点，
∴当x=0时，y=4
当y=0时，x=-2
∴点A（-2，0），点B（0，4）
如图：过点P作PE⊥x轴，交线段AB于点E
∴点E横坐标为-1，
∴y=-2+4=2
∴点E（-1，2）
∴|m-2|=1
∴m=3或1
故答案为：3或1
本题考查了一次函数图象上点的坐标特征，熟练运用一次函数的性质解决问题是本题的关键．
22、1
【解析】
这组数据的平均数为：（-1+1+0+1+3）÷5=1，所以方差=[（-1-1）1+（0-1）1+（1-1）1+（1-1）1+（3-1）1]=1．
23、1
【解析】
由DE是AB边的垂直平分线，可得AE=BE，又由在直角△ABC中，∠BAC=90°，AB=8，AC=6，利用勾股定理即可求得BC的长，继而由△ACE的周长=AC+BC，求得答案．
【详解】
解：∵DE是AB边的垂直平分线，
∴AE=BE，
∵在直角△ABC中，∠BAC=90°，AB=8，AC=6，
∴BC==10，
∴△ACE的周长为：AC+AE+CE=AC+BE+CE=AC+BC=6+10=1．
故答案为：1．
本题考查,线段垂直平分线的性质以及勾股定理．此题难度不大，注意掌握数形结合思想与转化思想的应用．
二、解答题（本大题共3个小题，共30分）
24、（1）作图见解析；（1）作图见解析.
【解析】
分析: （1）根据中心对称的性质画出△A1B1C1，再写出A1的坐标即可；
（1）根据点P、P′的坐标确定出平移规律，再求出A1、B1、C1的坐标,根据网格结构找出点A1、B1、C1的位置，然后顺次连接即可
详解:(1)如图，
A1的坐标为（1，-3）.
（1）
点睛: 本题考查了利用平移变换作图,中心对称变换作图，熟练掌握网格结构准确找出对应点的位置是解题的关键
25、（1）A区的的空气污染指数的平均数是79，B区的的空气污染指数的平均数是80；（2）A区
【解析】
（1）根据平均数的计算公式分别进行计算即可；
（2）根据平均数和众数的定义先求出各地区的平均数和众数，再进行比较即可得出答案．
【详解】
（1）A区的空气污染指数的平均数是：（115+108+85+100+95+50+80+70+50+50+100+45）=79；
B区的空气污染指数的平均数是：（105+95+90+80+90+60+90+85+60+70+90+45）=80；
（2）∵A区的众数是50，B区的众数是90，
∴A地区的环境状况较好．
∵A区的平均数小于B区的平均数，
∴A区的环境状况较好．
此题主要考查统计的有关知识，主要包括平均数、中位数、众数、方差的意义，熟记定义和计算公式是解题的关键．
26、5
【解析】
解：原式=．
取a=2，原式．
先根据分式混合运算的法则把原式进行化简，再选取合适的a的值（使分式的分母和除式不为0）代入进行计算即可．
题号
一
二
三
四
五
总分
得分
批阅人
每人加工件数
540
450
300
240
210
120
人数
1
1
2
6
3
2
月份
地区
区
区