辽宁省大连市名校2025届九上数学开学学业质量监测模拟试题【含答案】

这是一份辽宁省大连市名校2025届九上数学开学学业质量监测模拟试题【含答案】，共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）下列等式成立的是( )
A． •＝B．＝2C．﹣＝D．＝﹣3
2、（4分）如图，正方形ABCD中，AB=12，点E在边CD上，且BG=CG，将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG、CF，下列结论：①△ABG≌△AFG；②∠EAG=45°；③CE=2DE；④AG∥CF；⑤S△FGC=.其中正确结论的个数是（ ）
A．2个B．3个C．4个D．5个
3、（4分）若反比例函数，在每个象限内y随x的增大而减小，则m的取值范围是（ ）
A．m＞B．m＜C．m＞一D．m＜一
4、（4分）式子在实数范围内有意义，则的取值范围是（ ）
A．B．C．D．
5、（4分）某鞋店试销一款学生运动鞋，销量情况如图所示，鞋店经理要关心哪种型号的鞋是否畅销，下列统计量最有意义的是（ ）
A．平均数B．中位数C．众数D．方差
6、（4分）已知x（x﹣2）＝3，则代数式2x2﹣4x﹣7的值为（ ）
A．6B．﹣4C．13D．﹣1
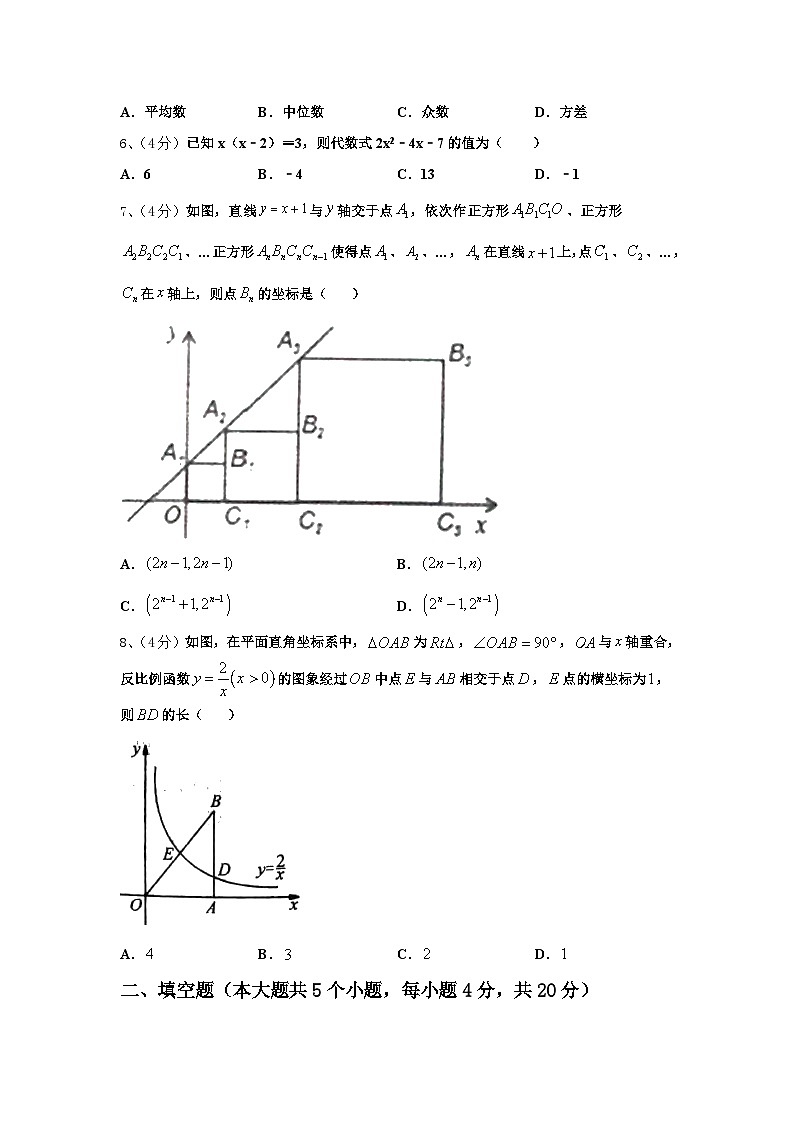
7、（4分）如图，直线与轴交于点，依次作正方形、正方形、…正方形使得点、、…，在直线上，点、、…，在轴上，则点的坐标是（ ）
A．B．
C．D．
8、（4分）如图，在平面直角坐标系中，为，，与轴重合，反比例函数的图象经过中点与相交于点，点的横坐标为，则的长（ ）
A．B．C．D．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图，四边形为正方形，点分别为的中点，其中，则四边形的面积为________________________．
10、（4分）如图，在四边形ABCD中，AD∥BC，AD=4，BC=12，点E是BC的中点．点P、Q分别是边AD、BC上的两点，其中点P以每秒个1单位长度的速度从点A运动到点D后再返回点A，同时点Q以每秒2个单位长度的速度从点C出发向点B运动．当其中一点到达终点时停止运动．当运动时间t为_____秒时，以点A、P，Q，E为顶点的四边形是平行四边形．
11、（4分）方程的解是_______．
12、（4分）一组数据15、13、14、13、16、13的众数是______，中位数是______.
13、（4分）如图，的面积为36,边cm，矩形DEFG的顶点D、G分别在AB、AC上，EF在BC上，若，则______cm.
三、解答题（本大题共5个小题，共48分）
14、（12分） (1)先化简，再求值：，其中
(2)解方程：
15、（8分）某商场欲购进果汁饮料和碳酸饮料共60箱，两种饮料每箱的进价和售价如下表所示。设购进果汁饮料x箱（x为正整数），且所购进的两种饮料能全部卖出，获得的总利润为W元（注：总利润＝总售价－总进价）。
（1）设商场购进碳酸饮料y箱，直接写出y与x的函数解析式；
（2）求总利润w关于x的函数解析式；
（3）如果购进两种饮料的总费用不超过2100元，那么该商场如何进货才能获利最多？并求出最大利润。
16、（8分）如图，在▱ABCD中，∠BAD的角平分线交BC于点E，交DC的延长线于点F，连接DE．
（1）求证：DA＝DF；
（2）若∠ADE＝∠CDE＝30°，DE＝2，求▱ABCD的面积．
17、（10分）如图，在 ABC ，C  90，AC＜BC，D 为 BC 上一点，且到 A、B 两点的距离相等．
（1）用直尺和圆规，作出点 D 的位置（不写作法，保留作图痕迹）；
（2）连结 AD，若 B  36 ，求∠CAD 的度数．
18、（10分）如图，在矩形ABCD中，，．将矩形ABCD沿过点C的直线折叠，使点B落在对角线AC上的点E处，折痕交AB于点F．
（1）求线段AC的长．
（2）求线段EF的长．
（3）点G在线段CF上，在边CD上存在点H，使以E、F、G、H为顶点的四边形是平行四边形，请画出，并直接写出线段DH的长．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）将直线y=2x-3平移，使之经过点(1，4)，则平移后的直线是____．
20、（4分）函数y=kx(k0)的图象上有两个点A1(，)，A2(，)，当，写出一个满足条件的函数解析式______________.
21、（4分）将直线y=2x-3向上平移5个单位可得______直线．
22、（4分）直角三角形有两边长为3和4，则斜边长为_____．
23、（4分）某商店销售型和型两种电脑，其中型电脑每台的利润为400元，型电脑每台的利润为500元，该商店计划一次性购进两种型号的电脑共100台，设购进型电脑台，这100台电脑的销售总利润为元，则关于的函数解析式是____________.
二、解答题（本大题共3个小题，共30分）
24、（8分）如图，边长为5的正方形OABC的顶点O在坐标原点处，点A，C分别在x轴、y轴的正半轴上，点E是OA边上的点(不与点A重合)，EF⊥CE，且与正方形外角平分线AG交于点P.
(1)求证：CE=EP.
(2)若点E的坐标为(3，0)，在y轴上是否存在点M，使得四边形BMEP是平行四边形?若存在，求出点M的坐标；若不存在，说明理由.
25、（10分）我们定义：如果两个三角形的两组对应边相等，且它们的夹角互补，我们就把其中一个三角形叫做另一个三角形的“夹补三角形”，同时把第三边的中线叫做“夹补中线．例如：图1中，△ABC与△ADE的对应边AB＝AD，AC＝AE，∠BAC+∠DAE＝180°，AF是DE边的中线，则△ADE就是△ABC的“夹补三角形”，AF叫做△ABC的“夹补中线”．
特例感知：
（1）如图2、图3中，△ABC与△ADE是一对“夹补三角形”，AF是△ABC的“夹补中线”；
①当△ABC是一个等边三角形时，AF与BC的数量关系是： ；
②如图3当△ABC是直角三角形时，∠BAC＝90°，BC＝a时，则AF的长是 ；
猜想论证：
（2）在图1中，当△ABC为任意三角形时，猜想AF与BC的关系，并给予证明．
拓展应用：
（3）如图4，在四边形ABCD中，∠DCB＝90°，∠ADC＝150°，BC＝2AD＝6，CD＝，若△PAD是等边三角形，求证：△PCD是△PBA的“夹补三角形”，并求出它们的“夹补中线”的长．
26、（12分）如图，▱ABCD中，E为BC边的中点，连AE并与DC的延长线交于点F，求证：DC＝CF．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、B
【解析】
利用二次根式的乘法法则对、进行判断；利用二次根式的加减法对进行判断；利用二次根式的性质对进行判断．
【详解】
解：、原式，所以选项错误；
、原式，所以选项正确；
、原式，所以选项错误；
、原式，所以选项错误．
故选：．
本题考查了二次根式的混合运算：先把二次根式化为最简二次根式，然后进行二次根式的乘除运算，再合并即可．在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．
2、D
【解析】
根据翻折变换的性质和正方形的性质可证Rt△ABG≌Rt△AFG；根据角的和差关系求得∠GAF=45°；在直角△ECG中，根据勾股定理可证CE=2DE；通过证明∠AGB=∠AGF=∠GFC=∠GCF，由平行线的判定可得AG∥CF；求出S△ECG，由S△FCG=即可得出结论．
【详解】
①正确．理由：
∵AB=AD=AF，AG=AG，∠B=∠AFG=90°，∴Rt△ABG≌Rt△AFG（HL）；
②正确．理由：
∵∠BAG=∠FAG，∠DAE=∠FAE．
又∵∠BAD=90°，∴∠EAG=45°；
③正确．理由：
设DE=x，则EF=x，EC=12-x．在直角△ECG中，根据勾股定理，得：（12﹣x）2+62=（x+6）2，解得：x=4，∴DE=x=4，CE=12-x=8，∴CE=2DE；
④正确．理由：
∵CG=BG，BG=GF，∴CG=GF，∴∠GFC=∠GCF．
又∵Rt△ABG≌Rt△AFG，∴∠AGB=∠AGF，∠AGB+∠AGF=2∠AGB=∠GFC+∠GCF=2∠GFC=2∠GCF，∴∠AGB=∠AGF=∠GFC=∠GCF，∴AG∥CF；
⑤正确．理由：
∵S△ECG=GC•CE=×6×8=1．
∵S△FCG===．
故选D．
本题考查了翻折变换的性质和正方形的性质，全等三角形的判定与性质，勾股定理，平行线的判定，三角形的面积计算等知识．此题综合性较强，难度较大，解题的关键是注意数形结合思想与方程思想的应用．
3、A
【解析】
根据反比例函数的性质可得关于m的不等式，解不等式即可求得答案.
【详解】
由题意得：2m-1>0，
解得：m>，
故选A.
本题考查了反比例函数的性质，①、当k＞0时，图象分别位于第一、三象限；当k＜0时，图象分别位于第二、四象限．②、当k＞0时，在同一个象限内，y随x的增大而减小；当k＜0时，在同一个象限，y随x的增大而增大．
4、D
【解析】
根据二次根式有意义的条件（被开方数≥0），列出不等式求解即可得到答案；
【详解】
解：式子在实数范围内有意义，
即： ，
解得：，
故选：D；
本题主要考查了二次根式有意义的条件，掌握二次根式有意义即被开方数≥0是解题的关键.
5、C
【解析】
众数是一组数据中出现次数最多的数，可能不止一个，对这个鞋店的经理来说，他最关注的是数据的众数．
【详解】
对这个鞋店的经理来说，他最关注的是哪一型号的卖得最多，即是这组数据的众数．
故选：C．
此题主要考查统计的有关知识，主要包括平均数、中位数、众数、方差的意义．反映数据集中程度的平均数、中位数、众数各有局限性，因此要对统计量进行合理的选择和恰当的运用．
6、D
【解析】
将x（x﹣2）=3代入原式=2x（x﹣2）﹣7，计算即可得到结论．
【详解】
当x（x﹣2）=3时，原式=2x（x﹣2）﹣7=2×3﹣7=6﹣7=﹣1．
故选D．
本题考查了代数式求值，解题的关键是掌握整体代入思想的运用．
7、D
【解析】
先求出直线y＝x＋1与y轴的交点坐标即可得出A1的坐标，故可得出OA1的长，根据四边形A1B1C1O是正方形即可得出B1的坐标，再把B1的横坐标代入直线y＝x＋1即可得出A1的坐标，同理可得出B2，B3的坐标，可以得到规律：Bn（2n−1，2n−1），据此即可求解．
【详解】
解：∵令x＝0，则y＝1，
∴A1（0，1），
∴OA1＝1．
∵四边形A1B1C1O是正方形，
∴A1B1＝1，
∴B1（1，1）．
∵当x＝1时，y＝1＋1＝2，
∴B2（3，2）；
同理可得，B3（7，4）；
∴B1的纵坐标是：1＝20，B1的横坐标是：1＝21−1，
∴B2的纵坐标是：2＝21，B2的横坐标是：3＝22−1，
∴B3的纵坐标是：4＝22，B3的横坐标是：7＝23−1，
∴Bn的纵坐标是：2n−1，横坐标是：2n−1，
则Bn
故选：D．
本题考查了一次函数图象上点的坐标特征、正方形的性质和坐标的变化规律．此题难度较大，注意正确得到点的坐标的规律是解题的关键．
8、B
【解析】
把E点的横坐标代入，确定E的坐标，根据题意得到B的坐标为（2，4），把B的横坐标代入求得D的纵坐标，就可求得AD，进而求得BD.
【详解】
解：反比例函数的图象经过OB中点E，E点的横坐标为1，
，
∴E（1，2），
∴B（2，4），
∵△OAB为Rt△，∠OAB=90°，
∴AB=4，
把x=2代入得，
∴AD=1，
∴BD=AB-AD=4-1=3，
故选：B．
此题考查了反比例函数与一次函数的交点问题、反比例函数图象上点的坐标特征、三角形中位线性质，解题的关键是求得B、D的纵坐标．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、4.
【解析】
先判定四边形EFGH为矩形，再根据中位线的定理分别求出EF、EH的长度，即可求出四边形EFGH的面积.
【详解】
解：∵四边形ABCD是正方形，点E、F、G、H分别是AB、BC、CD、DA的中点，
∴△AEH、△BEF、△CFG、△DGH都为等腰直角三角形，
∴∠HEF、∠EFG、∠FGH、∠GHE都为直角，
∴四边形EFGH是矩形，
边接AC，则AC=BD=4，
又∵EH是△ABD的中位线，
∴EH=BD=2，
同理EF=AC=2，
∴四边形EFGH的面积为2×2=4.
故答案为4.
本题考查了正方形的性质，矩形的判定，三角形中位线定理.
10、2或.
【解析】
分别从当Q运动到E和B之间与当Q运动到E和C之间去分析, 根据平行四边形的性质, 可得方程, 继而可求得答案.
【详解】
解：E是BC的中点,
BE=CE=BC=12=6,
①当Q运动到E和C之间, 设运动时间为t, 则AP=t, DP=AD-AP=4-t, CQ=2t,EQ=CE-CQ=6-2t
t=6-2t,
解得: t=2;
②当Q运动到E和B之间,设运动时间为t,则AP=t, DP=AD-AP=4-t, CQ=2t,
EQ=CQ-CE=2t-6,
t=2t-6,
解得: t=6（舍），
③P点当D后再返回点A时候，Q运动到E和B之间,设运动时间为t，
则AP=4-（t-4）=8-t, EQ=2t-6，
8-t=2t-6，,
当运动时间t为2、秒时,以点P,Q,E，A为顶点的四边形是平行四边形．
故答案为: 2或.
本题主要考查平行四边形的性质及解一元一次方程.
11、
【解析】
观察可得最简公分母是，方程两边乘最简公分母，可以把分式方程转化为整式方程求解．
【详解】
解：两边同时乘以得，
，
解得，，
检验：当时，，不是原分式方程的解；
当时，，是原分式方程的解．
故答案为：．
本题考查了解分式方程：（1）解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．（2）解分式方程一定注意要验根．
12、13 13.5
【解析】
这组数据中出现次数最多的数为众数；把这组数按从小到大的顺序排列，因为数的个数是偶数个，那么中间两个数的平均数即是中位数由此解答．
【详解】
解：∵15、13、14、13、16、13中13出现次数最多有3次，
∴众数为13，
将这组数从小到大排列为：13，13，13，14，15，16，最中间的两个数是13，14，所以中位数=（13+14）÷2=13.5
故答案为：13；13.5.
此题主要考查了中位数和众数的含义．
13、6
【解析】
作AH⊥BC于H点，可得△ADG∽△ABC，△BDE∽△BAH，根据相似三角形对应边比例等于相似比可解题．
【详解】
解：作AH⊥BC于H点，
∵四边形DEFG为矩形，
∴△ADG∽△ABC，△BDE∽△BAH，
∵的面积为36,边cm
∴AH=6
∵EF=2DE，即DG=2DE
解得：DE=3
∴DG=6
故答案为：6
本题考查了相似三角形的判定，考查了相似三角形对应边比例相等的性质．
三、解答题（本大题共5个小题，共48分）
14、 (1) ， ；(2).
【解析】
(1)先进行除法运算，再通分进行化简，将 代入化简结果即可得到答案；
(2) 方程两边都乘以，再移项，系数化为1，检验根的正确性，得到答案.
【详解】
(1)



当时，原式
(2)解方程：
解：方程两边都乘以，得

解这个方程，得
检验：将代入原方程
左边＝右边＝1
∴原方程的根是
本题考查分式的化简和解分式方程，解题的关键是掌握分式的化简和解分式方程的方法.
15、（1）y＝60－x；（2）w＝5x＋420；（3）该商场购进两种饮料分别为40箱和20箱时，能获得最大利润620元.
【解析】
(1)根据购进果汁饮料和碳酸饮料共60箱即可求解;
(2)根据总利润=每个的利润数量就可以表示出w与x之间的关系式;
(3)由题意得40x＋25（60－x）≤2100,解得x的值,然后可求y值,根据一次函数的性质可以求出进货方案及最大利润.
【详解】
（1）y与x的函数解析式为y＝60－x.
（2）总利润w关于x的函数解析式为
w＝（52－40）x＋（32－25）（60－x）＝5x＋420.
（3）由题意得40x＋25（60－x）≤2100，解得x≤40，
∵y＝5x＋420，y随x的增大而增大，
∴当x＝40时，y最大值＝5×40＋420＝620（元），
此时购进碳酸饮料60-40=20（箱）.
∴该商场购进两种饮料分别为40箱和20箱时，能获得最大利润620元.
本题考查了一次函数的实际运用,由销售问题的数量关系求出函数的解析式,列一元一次不等式解实际问题的运用,一次函数的性质的运用,解答时求出函数的解析式是关键.
16、（1）详见解析；（1）4
【解析】
（1）根据平行四边形的性质得出AB=CD，AD∥BC，求出∠FAD=∠AFB，根据角平分线定义得出∠FAD=∠FAB，求出∠AFB=∠FAB，即可得出答案；
（1）求出△ABF为等边三角形，根据等边三角形的性质得出AF=BF=AB，∠ABE=60°，在Rt△BEF中，∠BFA=60°，BE=，解直角三角形求出EF=1，BF=4，AB=BF=4，BC=AD=1，即可得出答案．
【详解】
（1）证明：∵四边形ABCD为平行四边形，
∴AB∥CD．
∴∠BAF＝∠F．
∵AF平分∠BAD，
∴∠BAF＝∠DAF．
∴∠F＝∠DAF．
∴AD＝FD．
（1）解：∵∠ADE＝∠CDE＝30°，AD＝FD，
∴DE⊥AF．
∵tan∠ADE＝，
∴AE＝1．
∴S平行四边形ABCD＝1S△ADE＝AE•DE＝4．
本题考查了平行四边形的性质及解直角三角形的知识，体现了转化的数学思想，难度不大．
17、 (1)作图见解析；（2）18°
【解析】
分析：（1）根据“到A，B两点的距离相等”可知点D在线段AB的中垂线上，据此作AB中垂线与BC交点可得；
（2）先根据直角三角形的性质得∠CAB=54°，再由DA=DB知∠B=∠DAB=36°，从而根据∠CAD=∠CAB﹣∠DAB可得答案．
详解：（1）如图所示，点D即为所求；

（2）在△ABC中，∵∠C=90°，∠B=36°，∴∠CAB=54°，由（1）知DA=DB，∴∠B=∠DAB=36°，则∠CAD=∠CAB﹣∠DAB=18°．
点睛：本题主要考查作图﹣复杂作图，解题的关键是掌握线段垂直平分线的性质和等边对等角的性质．
18、（1）；（2）；（3）见解析，.
【解析】
（1）根据勾股定理计算AC的长；
（2）设EF=x，在Rt△AEF中，由勾股定理列方程可解答；
（3）先正确画图，根据折叠的性质和平行线的性质证明CH=GH可解答．
【详解】
解：（1）∵四边形ABCD矩形，.
在中，；
（2）设EF的长为x．
由折叠，得，，，
，，，
在中，，即，
解得．．
（3）如图，∵四边形EFGH是平行四边形，
∴EF∥GH，EF=GH=3，
∴∠EFC=∠CGH，
∵AB∥CD，
∴∠BFC=∠DCF，
由折叠得：∠BFC=∠EFC，
∴∠CGH=∠DCF，
∴CH=GH=3，
∴DH=CD-CH=8-3=1．
故答案为：（1）；（2）；（3）见解析，.
本题是四边形的综合题目，考查了矩形的性质、折叠的性质、平行四边形的性质、平行线的性质、勾股定理等知识；熟练掌握矩形的性质和折叠的性质，由勾股定理得出方程是解决问题的关键．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、y=2x+2
【解析】
【分析】先由平移推出x的系数是2，可设直线解析式是y=2x+k,把点（1，4）代入可得.
【详解】由已知可设直线解析式是y=2x+k,
因为，直线经过点（1，4）,
所以，4=2+k
所以，k=2
所以，y=2x+2
故答案为y=2x+2
【点睛】本题考核知识点：一次函数性质.解题关键点：熟记一次函数性质.
20、y=-x(k