江苏省海安市八校2024-2025学年九上数学开学达标测试试题【含答案】

这是一份江苏省海安市八校2024-2025学年九上数学开学达标测试试题【含答案】，共25页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）如图，两地被池塘隔开，小明先在直线外选一点，然后测量出，的中点，并测出的长为．由此，他可以知道、间的距离为（ ）
A．B．C．D．
2、（4分）一组数据：3，2，5，3，7，5，x，它们的众数为5，则这组数据的中位数是（ ）
A．2B．3C．5D．7
3、（4分）已知直角三角形的两直角边长分别为5和12，则此直角三角形斜边上的中线长为（）
A．B．6C．13D．
4、（4分）已知一次函数y=kx+b，-3A．2B．3或0C．4D．2成0
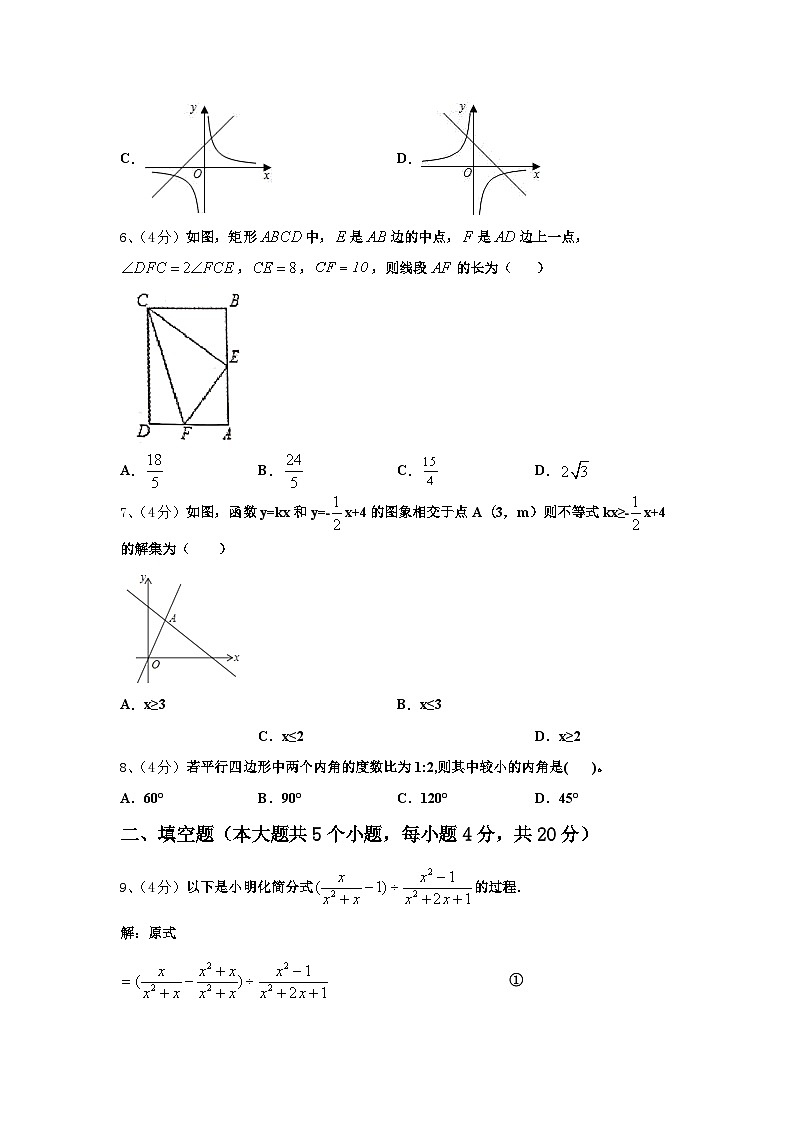
5、（4分）函数y＝x+m与y＝（m≠0）在同一坐标系内的图象可以是（ ）
A．B．
C．D．
6、（4分）如图，矩形中，是边的中点，是边上一点，，，，则线段的长为（ ）
A．B．C．D．
7、（4分）如图，函数y=kx和y=﹣x+4的图象相交于点A（3，m）则不等式kx≥﹣x+4的解集为（ ）
A．x≥3 B．x≤3 C．x≤2 D．x≥2
8、（4分）若平行四边形中两个内角的度数比为1:2,则其中较小的内角是( )。
A．60°B．90°C．120°D．45°
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）以下是小明化简分式的过程．
解：原式
①
②
③
④
（1）小明的解答过程在第_______步开始出错；
（2）请你帮助小明写出正确的解答过程，并计算当时分式的值．
10、（4分）已知实数满足，则以的值为两边长的等腰三角形的周长是_________________.
11、（4分）如图在中，，，的平分线交于，交的延长线于，则的值等于_________.
12、（4分）如图，先画一个边长为1的正方形，以其对角线为边画第二个正方形，再以第二个正方形的对角线为边画第三个正方形，…，如此反复下去，那么第n个正方形的对角线长为_____．
13、（4分）如图，平行四边形ABCD中，AC⊥AB，点E为BC边中点，AD=6，则AE的长为________．
三、解答题（本大题共5个小题，共48分）
14、（12分）如图，在△ABC中，∠ACB=90°，且DE是△ABC的中位线．延长ED到F，使DF=ED，连接FC，FB．回答下列问题：
（1）试说明四边形BECF是菱形．
（2）当的大小满足什么条件时，菱形BECF是正方形？请回答并证明你的结论．

15、（8分）（已知：如图1，矩形OACB的顶点A，B的坐标分别是（6，0）、（0，10），点D是y轴上一点且坐标为（0，2），点P从点A出发以每秒1个单位长度的速度沿线段AC﹣CB方向运动，到达点B时运动停止．
（1）设点P运动时间为t，△BPD的面积为S，求S与t之间的函数关系式；
（2）当点P运动到线段CB上时（如图2），将矩形OACB沿OP折叠，顶点B恰好落在边AC上点B′位置，求此时点P坐标；
（3）在点P运动过程中，是否存在△BPD为等腰三角形的情况？若存在，求出点P坐标；若不存在，请说明理由．
16、（8分）如图，将矩形沿折叠，使点恰好落在边的中点上，点落在处，交于点.若，，求线段的长.
17、（10分）如图，在菱形ABCD中，对角线AC，相交于点O，cm，cm，E，F分别是AB，BC的中点，点P是对角线AC上的一个动点，设cm，cm，cm
小明根据学习函数的经验，分别对这两种函数随自变量的变化而变化的情况进行了探究，下面是小明探究过程，请补充完整：
（1）画函数的图象
①按下表自变量的值进行取点、画图、测量，得到了与x的几组对应值：
②在所给坐标系中描出补全后的表中的各对应值为坐标的点，画出函数的图象；
（2）画函数的图象
在同一坐标系中，画出函数的图象；
（3）根据画出的函数的图象、函数的图象，解决问题
①函数的最小值是________________；
②函数的图象与函数的图象的交点表示的含义是________________；
③若，AP的长约为________________cm
18、（10分）某乡镇实施产业扶贫，帮助贫困户承包了荒山种植某品种蜜柚.到了收获季节，已知该蜜柚的成本价为8元/千克，投入市场销售时，调查市场行情，发现该蜜柚销售不会亏本，且每天销售量(千克)与销售单价(元/千克)之间的函数关系如图所示.
(1)求与的函数关系式，并写出的取值范围；
(2)当该品种蜜柚定价为多少时，每天销售获得的利润最大？最大利润是多少？
(3)某农户今年共采摘蜜柚4800千克，该品种蜜柚的保质期为40天，根据(2)中获得最大利润的方式进行销售，能否销售完这批蜜柚？请说明理由.
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）．若2m= 3n，那么m︰n= .
20、（4分）如图，已知点A(1，a)与点B(b，1)在反比例函数y＝(x＞0)图象上，点P(m，0)是x轴上的任意一点，若△PAB的面积为2，此时m的值是______．
21、（4分）分解因式：5x3﹣10x2=_______．
22、（4分）计算：=___________
23、（4分）如图，在中，，，点D在边上，若以、为边，以为对角线，作，则对角线的最小值为_______．
二、解答题（本大题共3个小题，共30分）
24、（8分）某住宅小区有一块草坪如图所示．已知AB＝3米，BC＝4米，CD＝12米，DA＝13米，且AB⊥BC，求这块草坪的面积．
25、（10分）如图，是的中线，，交于点，是的中点，连接.
（1）求证：四边形是平行四边形；
（2）若四边形的面积为，请直接写出图中所有面积是的三角形.
26、（12分）某公司欲招聘一名公务人员，对甲、乙两位应试者进行了面试和笔试，他们的成绩（百分制）如表所示：
（1）如果公司认为面试和笔试同等重要，从他们的成绩看，谁将被录取？
（2）如果公司认为作为公务人员面试成绩应该比笔试成绩更重要，并分别赋予它们6和4的权，计算甲、乙两人各自的平均成绩，谁将被录取？
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、D
【解析】
根据三角形中位线定理解答．
【详解】
解：∵点M，N分别是AC，BC的中点，
∴AB=2MN=13（m），
故选：C．
本题考查了三角形中位线定理，掌握三角形的中位线平行于第三边，且等于第三边的一半是关键．
2、C
【解析】
分析：众数是指一组数据中出现次数最多的那个数据，一组数据可以有多个众数，也可以没有众数；中位数是指将数据按大小顺序排列起来形成一个数列，居于数列中间位置的那个数据．根据定义即可求出答案．
详解：∵众数为5， ∴x=5， ∴这组数据为：2,3,3,5,5,5,7， ∴中位数为5， 故选C．
点睛：本题主要考查的是众数和中位数的定义，属于基础题型．理解他们的定义是解题的关键．
3、D
【解析】
已知直角三角形的两直角边长分别为5和12，根据勾股定理求得斜边为13，根据直角三角形斜边上的中线等于斜边的一半，得此直角三角形斜边上的中线长为，故选D.
4、D
【解析】
本题分情况讨论①x=-3时对应y=-1，x=1时对应y=3；②x=-3时对应y=3，x=1时对应y=-1；将每种情况的两组数代入即可得出答案．
【详解】
①将x=-3，y=-1代入得：-1=-3k+b，将x=1，y=3代入得：3=k+b，
解得：k=1，b=2；函数解析式为y=x+2，经检验验符合题意；
②将x=-3，y=3，代入得：3=-3k+b，将x=1，y=-1代入得：-1=k+b，
解得：k=-1，b=1，函数解析式为y=-x，经检验符合题意；
综上可得b=2或1．
故选D．
本题考查待定系数法求函数解析式，注意本题需分两种情况，不要漏解．
5、C
【解析】
根据一次函数y=x+m的图象必过一、三象限，可判断出选项B、D不符合题意，然后针对A、C选项，先根据一次函数的性质判断出m取值，再根据反比例函数的性质判断出m的取值，二者一致的即为正确答案．
【详解】
一次函数y=x+m中，k=1>0，所以函数图象必过一、三象限，观察可知B、D选项不符合题意；
A、由函数y=x+m的图象可知m＜0，由函数y=的图象可知m＞0，相矛盾，故错误；
C、由函数y=x+m的图象可知m>0，由函数y=的图象可知m＞0，正确，
故选C．
本题主要考查了反比例函数的图象性质和一次函数的图象性质，要掌握它们的性质才能灵活解题．
6、A
【解析】
延长﹑交于点，先证得得出，，再由勾股定理得，然后设，根据勾股定理列出方程得解.
【详解】
解：延长﹑交于点，
则，
∴，，
∵，
∴，
∴，
∴，
∴由勾股定理得，
设，
在和中，
则，
解得．
故选：A
本题考查了勾股定理的应用，添加辅助线构造全等三角形，运用勾股定理列出方程是解本题的关键.
7、A
【解析】
将点A(m,3)代入y=−x+4得,−m+4=3，
解得，m=2，
所以点A的坐标为(2,3)，
由图可知,不等式kx⩾−x+4的解集为x⩾2.
故选D
本题考查了一次函数和不等式（组）的关系以及数形结合思想的应用.解决此类问题的关键是仔细观察图形，注意几个关键点（交点、原点等），做到数形结合.
8、A
【解析】
首先设平行四边形中两个内角的度数分别是x°，2x°，由平行四边形的邻角互补，即可得方程x+2x=180，继而求得答案．
【详解】
设平行四边形中两个内角的度数分别是x°,2x°，
则x+2x=180，
解得：x=60，
∴其中较小的内角是：60°.
故选A.
此题考查平行四边形的性质，解题关键在于利用平行四边形的邻角互补.
二、填空题（本大题共5个小题，每小题4分，共20分）
9、 (1) ②；（2）2
【解析】
根据分式的混合运算法则进行计算即可.
【详解】
（1）②，应该是．
（2）解：原式=
．
当时，
此题考查分式的混合运算，解题关键在于掌握运算法则.
10、19
【解析】
先根据非负数的性质求得x、y的值，然后再根据等腰三角形的性质以及三角形三边关系进行讨论即可得.
【详解】
根据题意得，x-3=0，y-8=0，
解得x=3，y=8，
①3是腰长时，三角形的三边分别为3、3、8，
∵3+3<8，
∴不能组成三角形，
②3是底边时，三角形的三边分别为3、8、8，
能组成三角形，周长=3+8+8=19，
所以，三角形的周长为19，
故答案为：19.
本题了非负数的性质，等腰三角形的性质，三角形三边的关系，涉及了绝对值的非负性，二次根式的非负性，等腰三角形的性质等，求出x、y的值是解题的关键，难点在于要分情况讨论并且利用三角形的三边关系进行判断．
11、4
【解析】
根据平行四边形的性质得到∠F=∠DCF，根据角平分线的性质得到BF=BC=8，从而解得答案.
【详解】
∵四边形ABCD是平行四边形，
∴AB∥CD，AD=BC=8，CD=AB=6，
∴∠F=∠DCF，
∵∠C平分线为CF，
∴∠FCB=∠DCF，
∴∠F=∠FCB，
∴BF=BC=8，
同理：DE=CD=6，
∴AF=BF-AB=2，AE=AD-DE=2，
∴AE+AF=4；
本题考查平行四边形的性质和角平分线的性质，解题的关键是掌握平行四边形的性质和角平分线的性质.
12、（）n．
【解析】
第1个正方形的边长是1，对角线长为；第二个正方形的边长为，对角线长为（）2=2，第3个正方形的对角线长为（）3；得出规律，即可得出结果．
【详解】
第1个正方形的边长是1，对角线长为；
第二个正方形的边长为，对角线长为（）2＝2
第3个正方形的边长是2，对角线长为2＝（）3；…，
∴第n个正方形的对角线长为（）n；
故答案为（）n．
本题主要考查了正方形的性质、勾股定理；求出第一个、第二个、第三个正方形的对角线长，得出规律是解决问题的关键．
13、1
【解析】
由平行四边形的性质得出BC=AD=6，由直角三角形斜边上的中线性质即可得出结果．
【详解】
∵四边形ABCD是平行四边形，
∴BC=AD=6，
∵E为BC的中点，AC⊥AB，
∴AE=BC=1，
故答案为：1．
本题考查了平行四边形的性质、直角三角形斜边上的中线性质；熟练掌握平行四边形的性质，由直角三角形斜边上的中线性质求出AE是解决问题的关键．
三、解答题（本大题共5个小题，共48分）
14、（1）见解析；（2）当∠A=45°时，菱形BECF是正方形．
【解析】
分析：（1）根据已知条件发现：可以证明四边形的对角线互相垂直平分即是一个菱形．
（2）菱形要是一个正方形，则根据正方形的对角线平分一组对角，即∠BEF=45°，则∠A=45°．
详（1）证明：∵DE是△ABC的中位线，
∴DE∥AC．
又∵∠ACB=90°，
∴EF⊥BC．
又∵BD=CD，DF=ED，
∴四边形BECF是菱形．
（2）解：要使菱形BECF是正方形
则有BE⊥CE
∵E是△ABC的边AB的中点
∴当△CBA是等腰三角形时，满足条件
∵∠BCA=90°
∴△CBA是等腰直角三角形
∴当∠A=45°时，菱形BECF是正方形．
点睛：（1）熟悉菱形的判定方法；（2）探索性的试题，可以从若要满足结论，则需具备什么条件进行分析．
15、（1）S=（2） （3）存在，(6,6)或 ，
【解析】
（1）当P在AC段时，△BPD的底BD与高为固定值，求出此时面积；当P在BC段时，底边BD为固定值，用t表示出高，即可列出S与t的关系式；
（2）当点B的对应点B′恰好落在AC边上时，设P（m，10），则PB=PB′=m，由勾股定理得m2=22+（6-m）2，即可求出此时P坐标；
（3）存在，分别以BD，DP，BP为底边三种情况考虑，利用勾股定理及图形与坐标性质求出P坐标即可．
【详解】
解：（1）∵A，B的坐标分别是（6，0）、（0，10），
∴OA=6，OB=10，
当点P在线段AC上时，OD=2，BD=OB-OD=10-2=8，高为6，
∴S=×8×6=24；
当点P在线段BC上时，BD=8，高为6+10-t=16-t，
∴S=×8×（16-t）=-4t+64；
∴S与t之间的函数关系式为：；
（2）设P（m，10），则PB=PB′=m，如图1，
∵OB′=OB=10，OA=6，
∴AB′==8，
∴B′C=10-8=2，
∵PC=6-m，
∴m2=22+（6-m）2，
解得m=
则此时点P的坐标是（，10）；
（3）存在，理由为：
若△BDP为等腰三角形，分三种情况考虑：如图2，
①当BD=BP1=OB-OD=10-2=8，
在Rt△BCP1中，BP1=8，BC=6，
根据勾股定理得：CP1=，
∴AP1＝10−，
即P1（6，10-），
②当BP2=DP2时，此时P2（6，6）；
③当DB=DP3=8时，
在Rt△DEP3中，DE=6，
根据勾股定理得：P3E=，
∴AP3=AE+EP3=+2，
即P3（6，+2），
综上，满足题意的P坐标为（6，6）或（6，10-），（6，+2）．
本题是四边形综合题，考查了矩形的性质，坐标与图形性质，等腰三角形的性质，勾股定理等知识，注意分类讨论思想和方程思想的运用．
16、.
【解析】
先根据勾股定理求出BF，再根据△AMC′∽△BC′F求出AM即可．
【详解】
解：根据折叠的性质可知，FC=FC′，∠C=∠FC′M=90°，
设BF=x，则FC=FC′=9-x，
∵BF2+BC′2=FC′2，
∴x2+32=（9-x）2，
解得：x=4，即BF=4，
∵∠FC′M=90°，
∴∠AC′M+∠BC′F=90°，
又∵∠BFC′+BC′F=90°，
∴∠AC′M=∠BFC′，
∵∠A=∠B=90°，
∴△AMC′∽△BC′F，
，
∵BC′=AC′=3，
∴AM=．
本题主要考查了折叠的性质，矩形的性质，相似三角形的判定与性质，能够发现△AMC′∽△BC′F是解决问题的关键．
17、（1）①见解析；②见解析；（2）见解析；（3）①y1的最小值是0.5；②AP的长为2cm；③x=2.1．
【解析】
（1）①由表格得点（x，y1）即可；
②先由①描点，再用光滑曲线顺次连接各点，即可得出函数图象；利用数形结合，根据当x=0.5时，得出y1值，填入表格即可；
（2）过点F作FM⊥AC于M，由菱形的性质各三角形中位线性质求得FM=1，PM=3-x，所以y2=，再利用描点法画出y2的图象即可；
（3）①利用数形结合，由函数y1的图象求解即可；
②过点F作FM⊥AC于M，
可利用几何背景意义求解；
③因PC=AC-AP=4-x，由PE=PC，则y1=4-x，利用图象求解即可．
【详解】
解：（1）①如下表：图象如图所示：
②过点F作FM⊥AC于M，如图，
∵菱形ABCD，
∴AC⊥BD，
∴FM∥BD，
∵F是BC的中点，
∴M是OC的中点，
∴FM=1，OM=1，
∴PM=3-x，
∴PF2=PM2+MF2，
∴y2=，
利用描点法作出图象，如图所示：
（3）如上图；
①由图象可得：函数y1的最小值是0.5；
②答案不唯一，如，如：用几何背景意义可知：函数y1的图象与函数y2的图象的交点表示的含义是：当PE=PF=1.12cm时，由图象可得：AP的长为2cm；
③∵PC=AC-AP=4-x，
∵PE=PC，
∴y1=4-x，
利用图象可得：x=2.1．
故答案为①0.5；②当PE=PF=1.12cm时，AP的长为2cm；③2.1．
本题考查动点函数的函数图象，菱形的性质，以及勾股定理的应用．熟练掌握用描点法作函数图象是解题关键．
18、（1）（）；（2）定价为19元时，利润最大，最大利润是1210元.（3）不能销售完这批蜜柚.
【解析】
【分析】（1）根据图象利用待定系数法可求得函数解析式，再根据蜜柚销售不会亏本以及销售量大于0求得自变量x的取值范围；
（2）根据利润=每千克的利润×销售量，可得关于x的二次函数，利用二次函数的性质即可求得；
（3）先计算出每天的销量，然后计算出40天销售总量，进行对比即可得.
【详解】（1）设 ，将点（10，200）、（15，150）分别代入，
则，解得 ，
∴，
∵蜜柚销售不会亏本，∴，
又，∴ ，∴，
∴ ；
（2） 设利润为元，
则
=
=，
∴ 当 时， 最大为1210，
∴ 定价为19元时，利润最大，最大利润是1210元；
(3) 当 时，，
110×40=4400＜4800，
∴不能销售完这批蜜柚.
【点睛】 本题考查了一次函数的应用、二次函数的应用，弄清题意，找出数量间的关系列出函数解析式是解题的关键.
一、填空题（本大题共5个小题，每小题4分，共20分）
19、3︰2
【解析】
根据比例的性质将式子变形即可.
【详解】
，
，
故答案为： 3︰2
点睛：此题考查比例的知识
20、﹣1或3
【解析】
把点A(1，a)与点B(b，1)代入反比例函数y＝(x＞0)，求出A,B坐标，延长AB交x轴于点C，如图2，设直线AB的解析式为y＝mx+n，求出点C的坐标，用割补法求出PC的值，结合点C的坐标即可.
【详解】
解：∵点A(1，a)与点B(b，1)在反比例函数y＝(x＞0)图象上，
∴a＝2，b＝2，
∴点A(1，2)与点B(2，1)，
延长AB交x轴于点C，如图2，
设直线AB的解析式为y＝mx+n，
则有，
解得，
∴直线AB的解析式为y＝﹣x+1．
∵点C是直线y＝﹣x+1与x轴的交点，
∴点C的坐标为(1，0)，OC＝1，
∵S△PAB＝2，
∴S△PAB＝S△PAC﹣S△PBC＝×PC×2﹣×PC×1＝PC＝2，
∴PC＝2．
∵C(1，0)，P(m，0)，
∴|m﹣1|＝2，
∴m＝﹣1或3，
故答案为：﹣1或3．
本题考查的是反比例函数，熟练掌握反比例函数图像上点的特征是解题的关键.
21、5x2(x-2)
【解析】
5x3-10x2=2x2(x-2)
22、6
【解析】
先取绝对值符号、计算负整数指数幂和零指数幂，再计算加减可得；
【详解】
解：原式=1+1+4=6
故答案为：6
此题主要考查了实数运算，绝对值，负整数指数幂和零指数幂，正确化简各数是解题关键．
23、1
【解析】
由平行四边形的对角线互相平分、垂线段最短知，当OD⊥BC时，DE线段取最小值，由三角形中位线定理求出OD，即可得出DE的最小值．
【详解】
解：∵，，
根据勾股定理得，
∵四边形是平行四边形，
，
∴当取最小值时，线段最短，即时最短，
是的中位线，
，
，
故答案为：1．
本题考查了平行四边形的性质，勾股定理以及垂线段最短，此题难度适中，注意掌握数形结合思想的应用．
二、解答题（本大题共3个小题，共30分）
24、36平方米
【解析】
连接AC，根据勾股定理，求得AC，再根据勾股定理的逆定理，判断三角形ACD是直角三角形．这块草坪的面积等于两个直角三角形的面积之和．
【详解】
连接AC，如图，∵AB⊥BC，∴∠ABC=90°．
∵AB=3米，BC=4米，∴AC=5米．
∵CD=12米，DA=13米，∴CD2+AC2=144+25=169=132=DA2，∴∠ACD=90°，∴△ACD为直角三角形，∴草坪的面积等于=S△ABC+S△ACD=3×4÷2+5×12÷2=6+30=36（米2）．
本题考查了勾股定理和勾股定理的逆定理．
25、（1）见解析；（2），，，
【解析】
（1）首先证明△AFE≌△DFB可得AE=BD，进而可证明AE=CD，再由AE∥BC可利用一组对边平行且相等的四边形是平行四边形可得四边形ADCE是平行四边形；
（2）根据面积公式解答即可．
【详解】
证明：∵AD是△ABC的中线，
∴BD=CD，
∵AE∥BC，
∴∠AEF=∠DBF，
在△AFE和△DFB中，
，
∴△AFE≌△DFB（AAS），
∴AE=BD，
∴AE=CD，
∵AE∥BC，
∴四边形ADCE是平行四边形；
（2）∵四边形ABCE的面积为S，
∵BD=DC，
∴四边形ABCE的面积可以分成三部分，即△ABD的面积+△ADC的面积+△AEC的面积=S，
∴面积是S的三角形有△ABD，△ACD，△ACE，△ABE．
此题主要考查了平行四边形的判定，全等三角形的判定和性质．等腰三角形的判定和性质等知识，解题的关键是正确寻找全等三角形解决问题.
26、 (1)甲将被录取；(2)乙将被录取.
【解析】
（1）求得面试和笔试的平均成绩即可得到结论；
（2）根据题意先算出甲、乙两位应聘者的加权平均数，再进行比较，即可得出答案．
【详解】
解：（1）＝＝89（分），
＝＝87.5（分），
因为＞，
所以认为面试和笔试成绩同等重要，从他们的成绩看，甲将被录取；
（2）甲的平均成绩为：（86×6+90×4）÷10＝87.6（分），
乙的平均成绩为：（92×6+83×4）÷10＝88.4（分），
因为乙的平均分数较高，
所以乙将被录取．
此题考查了加权平均数的计算公式，解题的关键是：计算平均数时按6和4的权进行计算．
题号
一
二
三
四
五
总分
得分
批阅人
x/cm
0
0.5
1
1.5
2
2.5
3
3.5
4
/cm
1.12
0.5
0.71
1.12
1.58
2.06
2.55
3.04
应试者
面试
笔试
甲
86
90
乙
92
83
x／cm
0
0.5
1
1.5
2
2.5
3
3.5
4
y1／cm
1.12
0.71
0.5
0.71
1.12
1.58
2.06
2.55
3.04