北京市延庆区第一中学2024-2025学年高二上学期10月月考数学试卷(含答案)

这是一份北京市延庆区第一中学2024-2025学年高二上学期10月月考数学试卷(含答案)，共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题
1．在平面直角坐标系中,角以为始边,其终边经过点,则( )
A.B.C.2D.
2．已知向量,,且与方向相反,则( )
A.B.0C.D.
3．在中,,,,则( )
A.B.C.D.或
4．已知,且角,的终边关于y轴对称,则( )
A.B.C.D.
5．设l,m是两条不同的直线,是一个平面,则下列命题正确的是( )
A.若,,则B.若,,则
C.若,,则D.若,,则
6．在中,,,则“”是“的面积为”的( )
A.充分而不必要条件B.必要而不充分条件
C.充分必要条件D.既不充分也不必要条件
7．在长方体中,,与平面所成的角为,则该长方体的体积为( )
A.8B.C.D.
8．已知函数，的最小正周期为，最大值为，则函数的图象( )
A.关于直线对称B.关于点对称
C.关于直线对称D.关于点对称
9．在中，，，，P为所在平面内的动点，且，则的取值范围是( )
A.B.C.D.
10．在《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马.如图，已知四棱锥为阳马，且，底面ABCD.若E是线段AB上的点（不含端点），设SE与AD所成的角为，与底面ABCD所成的角为，二面角的平面角为，则( )
A.B.C.D.
二、填空题
11．向量,满足,,与的夹角为,则_____________.
12．在中,点M,N满足,.若,则_____________.
13．已知是任意角,且满足,则常数k的一个取值为____________.
14．楔体形构件在建筑工程上有广泛的应用.如图,某楔体形构件可视为一个五面体ABCDEF,其中面ABCD为正方形.若,,且EF与面ABCD的距离为,则该楔体形构件的体积为______________.
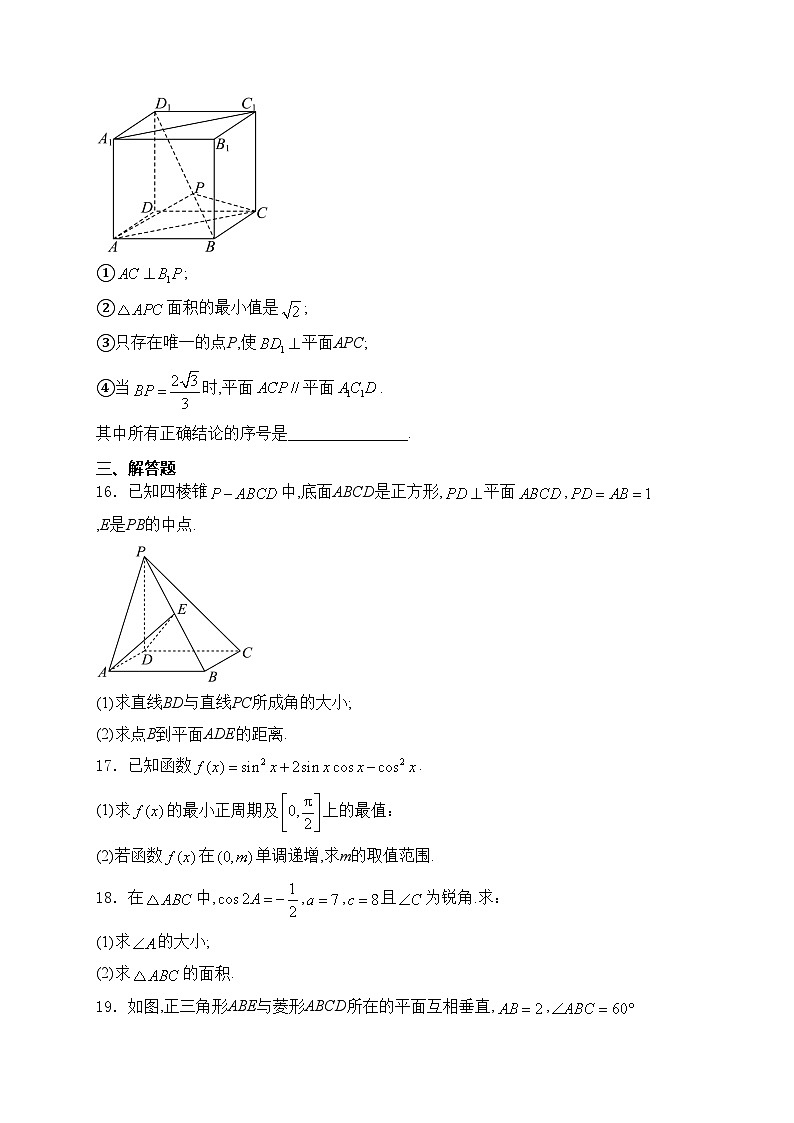
15．如图,在棱长为2的正方体中,点P是该正方体对角线上的动点,给出下列四个结论：
①;
②面积的最小值是;
③只存在唯一的点P,使平面APC;
④当时,平面平面.
其中所有正确结论的序号是_______________.
三、解答题
16．已知四棱锥中,底面ABCD是正方形,平面,,E是PB的中点.
(1)求直线BD与直线PC所成角的大小;
(2)求点B到平面ADE的距离.
17．已知函数.
(1)求的最小正周期及上的最值：
(2)若函数在单调递增,求m的取值范围.
18．在中,,,且为锐角.求：
(1)求的大小;
(2)求的面积.
19．如图,正三角形ABE与菱形ABCD所在的平面互相垂直,,,M是AB的中点.
(1)求二面角的余弦值;
(2)在线段EC上是否存在点P,使得直线AP与平面ABE所成的角为？若存在,求出的值;若不存在,说明理由.
20．如图,三棱柱中,四边形是边长为4的菱形,,点D为棱AC上动点（不与A,C重合）,平面与棱交于点E.
(1)求证：;
(2)若,从条件①、条件②、条件③中选择两个条件作为已知,求直线与平面所成角的正弦值.
条件①：
条件②：二面角为直二面角
条件③：.
21．定义向量的“伴随函数”为;函数的“伴随向量”为.
(1)写出函数的“伴随向量”为,并求;
(2)已知的“伴随函数”为,的“伴随函数”为,设,且的伴随函数为,其最大值为p.
①若,求p的取值范围;
②求证：向量的充要条件是.
参考答案
1．答案：A
解析：由三角函数的定义可知,
故选：A.
2．答案：D
解析：由题可知与是共线向量且方向相反,
所以,且,
所以,解得,(舍去)
故选：D.
3．答案：A
解析：由得,
由正弦定理得,,
解得,又,故,.
故选：A.
4．答案：B
解析：因为角,的终边关于y轴对称,所以,,
即,.
故选：B.
5．答案：B
解析：,,则,可能平行,A错;
,,由线面平行的性质可得,B正确;
,,则,l与m异面;C错,
,,l与m可能平行、相交、异面,D错,.
故选：B.
6．答案：C
解析：由已知在中,,,
若,则为正三角形,故,
若的面积为,则,,
又,即,,,
解得,故,
所以“”是“的面积为”的充分必要条件,
故选：C.
7．答案：C
解析：在长方体中,连接,

根据线面角的定义可知,
因为,所以,从而求得,
所以该长方体的体积为,
故选：C.
8．答案：C
解析：，其中，
因为函数的最小正周期为，所以，解得，
因为函数的最大值为，所以，解得(舍去)，
所以，
因为，
所以函数图象不关于直线对称，也不关于点对称，故AB错误；
因为，
所以函数图象关于直线对称，不关于点对称，故C正确，D错误.
故选：C.
9．答案：D
解析：以C为坐标原点，CA，CB所在直线分别为x轴，y轴建立平面直角坐标系，则，，设，则，，，所以，又表示圆上一点到点的距离的平方，圆心到点的距离为，所以，即，故选D.
10．答案：A
解析：在四棱锥中，E是线段AB上的点（不含端点），过E作交CD于点F，连接DE，SF，如图，
则是SE与AD所成的角，即，因为底面ABCD，则是SE与底面ABCD所成的角，即，
而底面ABCD，则，又ABCD是长方形，即，而，，平面SAD，
则平面SAD，又平面SAD，即有，得是二面角的平面角，即，
在中，，在中，，
由底面，底面ABCD可得，而，则有.
因为，，平面SCD，则平面SCD.又平面SCD，有，.
因为，，即有，因此，而正切函数在上递增，所以.故选A.
11．答案：2
解析：,
所以.
故答案为：2.
12．答案：
解析：在中,点M,N满足,,
,
,,
.
故答案为：.
13．答案：-3（答案不唯一）
解析：,满足,
,,得,,
当时,.
故答案为：-3（答案不唯一）
14．答案：
解析：由五面体ABCDEF可知,四边形与四边形都为平面四边形.
如图所示,分别取,的中点G,H,连接,,,

因为面为正方形,所以,
又平面,平面,
所以平面,
又平面平面,平面,
所以,
因为G,H分别为,的中点,,,
所以,,
则四边形为平行四边形,同理四边形也为平行四边形.
则,平面,平面,
所以平面,同理平面,又,
且平面,平面,
所以平面平面,又四边形也是平行四边形,
所以几何体为三棱柱,
已知EF与面ABCD的距离为,即点到平面的距离.
由题意,;
又;
所以该五面体的体积.
故答案为：.
15．答案：①③④
解析：①连接,在正方体中,
平面,平面,则,
又,,平面,平面,
则平面,又平面,则,①正确;
②设交于E,连接.由平面,得,
所以,
在中,当时,最小,
又,,,
,
此时,
因此面积的最小值为,②错误;
③连接,,由①知,平面,又平面,
所以,同理,
因为,平面,平面,
因此平面,
当点P为直线与平面的交点时,平面,
由于过一点A有且只有一个平面垂直于已知直线,
于是过直线与直线垂直的平面有且只有一个,
所以存在唯一的点P,使平面,③正确;
④当时,在中,,
,
则,
即,则,
又,,平面,平面,
所以平面,即平面,
由①同理可知,,,
且平面,平面,
因此平面,则平面平面,④正确,
故答案为：①③④.
16．答案：(1)
(2)
解析：(1)以点D为原点,分别以,,所在直线为x,y,z轴,
建立如图空间直角坐标系.

由题意,,,,,,
设直线BD与直线PC所成的角为,
因为,,
,
所以直线BD与直线PC所成角为;
(2)因为,,,
所以,
,
则为平面的一个法向量,
设点B到平面的距离为d,则d为向量在向量上的投影的绝对值,
由,得,
所以点B到平面的距离为.
17．答案：(1);最大值为,最小值为-1.
(2)
解析：(1)根据题意,
,
的最小正周期;
,,
则,即,
函数在区间上的最大值为,最小值为-1;
(2)由函数在单调递增,
令,得.
18．答案：(1)
(2)
解析：(1)因为,所以,所以,由得
所以,,
(2)由正弦定理,得,所以,
因为为锐角,所以,
所以存在且唯一确定.
因为,
所以
从而.
19．答案：(1)
(2)存在,且
解析：(1)连接,因为,M是中点,所以,
因为平面平面,平面平面,平面,
所以平面,而平面,所以,
因为三角形为正三角形,所以,
建立如图所示空间直角坐标系,
则,,,,,
所以,,
设是平面的一个法向量,则,
令,则,,所以,
由y轴与平面垂直,所以是平面的一个法向量,
所以,
所以二面角的余弦值为;
(2)假设在线段上存在点P,使得直线与平面所成角为,
,,
设,
则,
直线与平面所成的角为,
,则,
因为,所以,
所以在线段上存在点P使得直线与平面所成角为,且.
20．答案：(1)证明见解析;
(2)答案见解析.
解析：(1)在三棱柱中,,
又面,面,
所以平面,
又面面,面,
所以.
(2)若①②,取中点O,连接,,由题意易知,,
又二面角为直二面角,即面面,
因为面面,平面,所以面,
而平面,
所以,平面,
故,
由,则,
故可以以O为原点,以,,为x轴、y轴、z轴建立空间直角坐标系,
则由题意易知,,,,,
,,
所以,,,
设面的一个法向量为,则,
令,故,
设直线与面所成角为,
则,
所以直线与面所成角的正弦为;
若选②③：连接,取中点O,连接,,
在菱形中,
所以为等边三角形.
又O为中点,所以,
因为二面角为直二面角,即面面,
面面,平面,
所以平面,
因为平面,
故,
又,所以.
故可以以O为原点,以,,为x轴、y轴、z轴建立空间直角坐标系,
则由题意易知,,,,,
,,
所以,,,
设面的一个法向量为,则,
令,故,
设直线与面所成角为,
则,
所以直线与面所成角的正弦为;
若选①③,取中点O,连接,,
由题意易知,,
又在菱形中,所以为等边三角形.
又O为中点,所以,则,
而,
故可以以O为原点,以,,为x轴、y轴、z轴建立空间直角坐标系,
则由题意易知,,,,,
,,
所以,,,
设面的一个法向量为,则,
令,,故,
设直线与面所成角为,
则,
所以直线与面所成角的正弦为.
21．答案：(1),
(2)①;②证明见解析;
解析：(1)由题可知
故,所以
(2)①设,
由题可知,
所以
故
②先判断必要性,由题可知,
设,,
再判断充分性,
由
设
故
故
因为,
所以
所以有
因为,,所以,
所以,
因为,
得,
证得向量的充要条件是