

北师大版(2024)七年级上册数学期中复习第1—4章综合测试卷(含答案解析)
展开
这是一份北师大版(2024)七年级上册数学期中复习第1—4章综合测试卷(含答案解析),共18页。试卷主要包含了点P等内容,欢迎下载使用。
一.选择题(共30分)
1.在实数中,,,0.1010010001,中,无理数有( )个.
A.1B.2C.3D.4
2.点P(3+a,a+1)在x轴上,则点P坐标为( )
A.(2,0)B.(0,﹣2)C.(0,2)D.(﹣2,0)
3.下列各组数中能作为直角三角形的三边长的是( )
A.6,7,8B.5,6,7C.4.5,6,7.5D.4,5,6
4.若二次根式有意义,则x的取值范围是( )
A.x>0B.x≥2C.x≥0D.x>2
5.如图,在平面直角坐标系中,线段AC所在直线的解析式为y=﹣x+4,E是AB的中点,P是AC上一动点,则PB+PE的最小值是( )
A.B.C.D.
6.如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点C坐标是(5,2),则经过第2022次变换后点C的对应点的坐标为( )
A.(﹣5,﹣2)B.(5,﹣2)C.(﹣5,2)D.(5,2)
7.我市的用电量与应交电费之间的关系如表,则以下说法不正确的是( )
A.用电量每增加1千瓦时,应交电费就增加0.56元
B.在这个变化过程中,用电量和应交电费都是变量,其中应交电费是自变量
C.若用电量是3千瓦时的时候,应交电费是1.68元
D.应交电费是5.6元时,用电量是10千瓦时
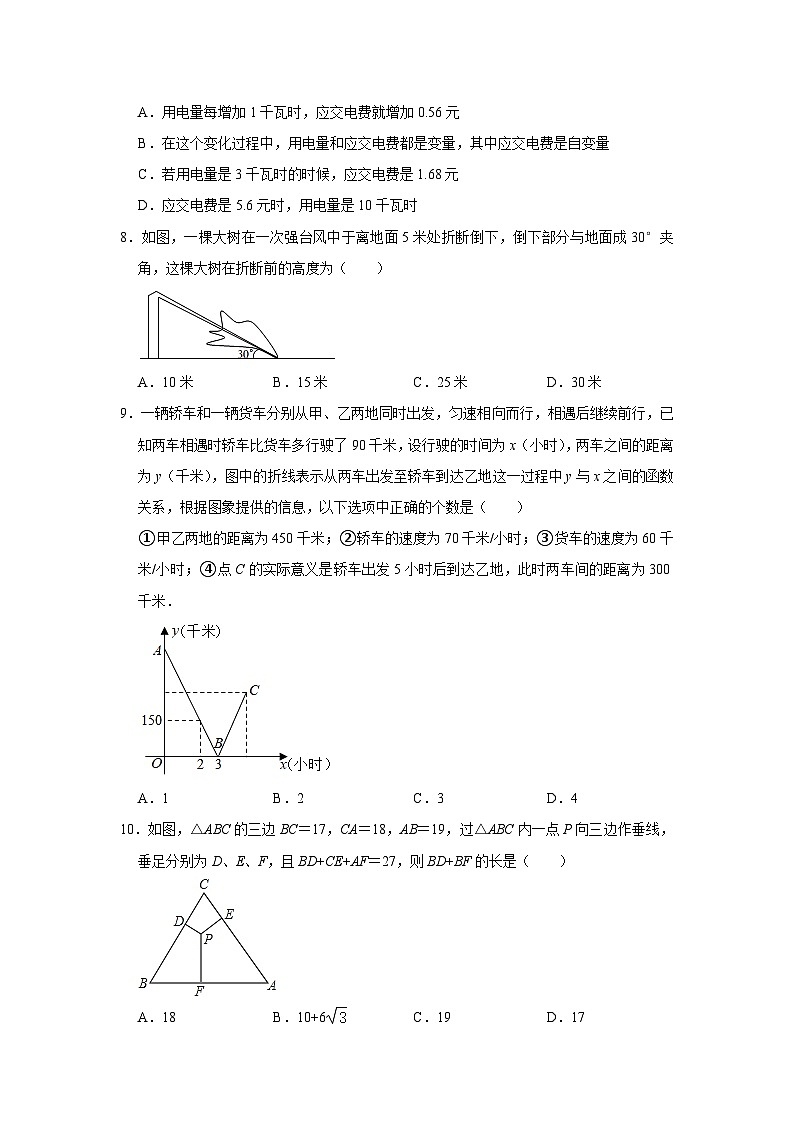
8.如图,一棵大树在一次强台风中于离地面5米处折断倒下,倒下部分与地面成30°夹角,这棵大树在折断前的高度为( )
A.10米B.15米C.25米D.30米
9.一辆轿车和一辆货车分别从甲、乙两地同时出发,匀速相向而行,相遇后继续前行,已知两车相遇时轿车比货车多行驶了90千米,设行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至轿车到达乙地这一过程中y与x之间的函数关系,根据图象提供的信息,以下选项中正确的个数是( )
①甲乙两地的距离为450千米;②轿车的速度为70千米/小时;③货车的速度为60千米/小时;④点C的实际意义是轿车出发5小时后到达乙地,此时两车间的距离为300千米.
A.1B.2C.3D.4
10.如图,△ABC的三边BC=17,CA=18,AB=19,过△ABC内一点P向三边作垂线,垂足分别为D、E、F,且BD+CE+AF=27,则BD+BF的长是( )
A.18B.10+6C.19D.17
二.填空题(共18分)
11.把2个面积为3的正方形纸片沿着对角线剪开,拼成如图所示的一个大正方形纸片,那么大正方形纸片的边长在 和 两个整数之间.
12.如果a,b分别是2021的两个平方根,那么a+b﹣ab= .
13.已知AB∥x轴,点A的坐标为(2,4),并且AB=3,则点B的坐标为 .
14.如图,已知在Rt△ABC中,∠ACB=90°,AB=12,分别以AC,BC为直径作半圆,面积分别记为S1、S2,则S1+S2等于 .
15.甲、乙两人分别加工100个零件,甲第1个小时加工了10个零件,之后每小时加工30个零件,乙在甲加工前已经加工了40个零件,在甲加工3小时后乙开始追赶甲,结果两人同时完成任务.设甲、乙两人各自加工的零件数为y(个),甲加工零件的时间为x(时),y与x之间的函数图象如图所示,当甲、乙两人相差15个零件时,甲加工零件的时间为 .
16.如图,在正方形ABCD的对角线AC上取一点E,使得∠CDE=15°,连接BE并延长BE到F,使CF=CB,BF与CD相交于点H,若AB=,有下列四个结论:①∠CBE=15°;②AE=+1;③S△DEC=;④CE+DE=EF.则其中正确的结论有 .(填序号)
三.解答题(共72分)
17.计算:
(1)|﹣2|+(﹣3)2﹣;
(2)﹣12021+|1+|﹣+.
18.已知x=+1,y=﹣1,求x2+3xy+y2的值.
19.如图所示的是某学校的平面示意图,已知旗杆的位置是(﹣1,2),实验室的位置是(2,3).
(1)根据所给条件建立适当的平面直角坐标系,并用坐标表示食堂宿舍楼和大门的位置.
(2)已知办公楼的位置是(﹣2,1),教学楼的位置是(3,1),在(1)中所画的图中标出办公楼和教学楼的位置.
20.为了解某种车的耗油量,我们对这种车在高速公路上做了耗油测验,并把测验的数据记录下来,表格如下:
(1)根据上表可知,该车油箱的大小为 升,每小时耗油 升.
(2)请求出两个变量之间的关系式(用t来表示Q):
(3)当汽车行驶了12小时,油箱还剩多少升油?
21.森林火灾是一种常见的自然灾害,危害很大,随着中国科技、经济的不断发展,开始应用飞机洒水的方式扑灭火源.如图,有一台救火飞机沿东西方向AB,由点A飞向点B,已知点C为其中一个着火点,且点C与直线AB上两点A,B的距离分别为600m和800m,又AB=1000m,飞机中心周围500m以内可以受到洒水影响.
(1)着火点C受洒水影响吗?为什么?
(2)若飞机的速度为10m/s,要想扑灭着火点C估计需要13秒,请你通过计算判断着火点C能否被扑灭?
22.如图,在三角形ABC中,AB=5,BC=6,AD为BC边上的中线,且AD=4,过点D作DE⊥AC于点E.
(1)求证:AD⊥BC;
(2)求DE的长.
23.甲、乙两地间的直线公路长为180千米,一辆摩托车和一辆轿车分别从甲、乙两地出发,沿该公路匀速行驶,已知轿车比摩托车早出发1小时,且轿车到达甲地停留t小时后原路原速返回乙地(调头时间忽略不计),最后两车同时到达乙地,在行驶过程中,两车距乙地的距离y(千米)与摩托车行驶的时间x(小时)的关系如图所示,请结合图象信息解答下列问题:
(1)轿车的速度是 千米/小时,摩托车的速度是 千米/小时,t的值为 ;
(2)写出摩托车距乙地的距离y(千米)与x(小时)的关系式;
(3)摩托车出发后几小时,两车在途中相距30千米?请直接写出答案.
24.阅读下列解题过程:
===﹣1;
===﹣.
请回答下列问题:
(1)归纳:观察上面的解题过程,请直接写出下列各式的结果.
①= ;②= ;
(2)应用:求++++…+的值;
(3)拓广:﹣+﹣= .
25.阅读:如图1,在△ABC中,3∠A+∠B=180°,BC=8,AC=10,求AB的长.
小明的思路:如图2,作BE⊥AC于点E,在AC的延长线上取点D,使得DE=AE,连接BD,易得∠A=∠D,△ABD为等腰三角形,由3∠A+∠B=180°和∠A+∠ABC+∠BCA=180°,易得∠BCA=2∠A,△BCD为等腰三角形,依据已知条件可得AE和AB的长.
解决下列问题:
(1)图2中,AE= ,AB= ;
(2)在△ABC中,∠A,∠B,∠C的对边分别为a、b、c.如图3,当3∠A+2∠B=180°时,用含a,c式子表示b.
参考答案
一.选择题(共30分)
1.解:,0.1010010001是分数,属于有理数;
,是整数,属于有理数;
无理数有,,共2个.
故选:B.
2.解:∵点P(3+a,a+1)在x轴上,
∴a+1=0,
∴a=﹣1,
3+a=2,
∴点P的坐标为(2,0).
故选:A.
3.解:A、∵62+72=85,82=64,
∴62+72≠82,
∴6,7,8不能作为直角三角形的三边长,
故A不符合题意;
B、∵52+62=61,72=49,
∴52+62≠72,
∴5,6,7不能作为直角三角形的三边长,
故B不符合题意;
C、∵4.52+62=56.25,7.52=56.25,
∴4.52+62=7.52,
∴4.5,6,7.5能作为直角三角形的三边长,
故C符合题意;
D、∵42+52=41,62=36,
∴42+52≠62,
∴4,5,6不能作为直角三角形的三边长,
故D不符合题意;
故选:C.
4.解:∵x﹣2≥0,
∴x≥2.
故选:B.
5.解:作点B关于AC的对称点B′,连接B′E交AC于P′,
此时,PB+PE=P′B+P′E的值最小,最小值为B′E的长,
∵线段AC所在直线的解析式为y=﹣x+4,
∴A(0,4),C(4,0),
∴AB=4,BC=4,
∵E是AB的中点,
∴E(0,2),
∵点B关于AC的对称点B′,
∴BB′⊥AC,OB=OB′=AC,AO=CO,
∴四边形ABCB′是正方形,
∴B′(4,4),
∴PB+PE的最小值是B′E==2.
故选:C.
6.解:点C第一次关于y轴对称后在第二象限,
点C第二次关于x轴对称后在第三象限,
点C第三次关于y轴对称后在第四象限,
点C第四次关于x轴对称后在第一象限,即点A回到原始位置,
所以,每四次对称为一个循环组依次循环,
∵2022÷4=505余2,
∴经过第2022次变换后所得的C点与第二次变换的位置相同,在第三象限,坐标为(﹣5,﹣2).
故选:A.
7.解:设用电量x(千瓦时),应缴电费y元,由表格中数据得到:y=0.56x.
∴用电量每增加1千瓦时,应缴电费增加0.56元正确.
∴A不合题意.
在这个变化过程中,应缴电费随用电量的增加而增加,电费单价不变,
∴用电量是自变量,应缴电费是因变量.
∴B符合题意.
∵当x=3时,y=0.56×3=1.68元.
∴C不合题意.
当y=5.6时,x=5.6÷0.56=10.
∴D不合题意.
故选:B.
8.解:∵∠BAC=30°,∠BCA=90°,BC=5米,
∴AB=2CB=10米,
∴这棵大树在折断前的高度为AB+BC=15米.
故选:B.
9.解:由图象可得,
甲、乙两地的距离为:150×3=450(千米),故①正确;
∵两车相遇时轿车比货车多行驶了90千米,
∴轿车每小时比货车多行驶90÷3=30(千米),
∴轿车的速度为:(450÷3+30)÷2=90(千米/小时),故②错误;
货车的速度为:(450÷3﹣30)÷2=60(千米/小时),故③正确;
点C的实际意义是轿车出发450÷90=5小时后到达乙地,此时两车间的距离为:(90+60)×(5﹣3)=300(千米),故④正确;
故选:C.
10.解:连接PA、PB、PC,
设BD=x,CE=y,AF=z,
则CD=17﹣x,EA=18﹣y,FB=19﹣z,
由勾股定理得,
x2+PD2=(19﹣z)2+PF2①,
同理得,y2+PE2=(17﹣x)2+PD2②,
z2+PF2=(18﹣y)2+PE2③,
①+②+③得,
x2+y2+z2=(17﹣x)2+(18﹣y)2+(19﹣z)2,
化简得,17x+18y+19z=487,
∵x+y+z=27,
∴x=z﹣1,
∴BD+BF=x+(19﹣z)=18,
故选:A.
二.填空题(共18分)
11.解:由题意可知大正方形的面积为6,因此边长为,
而2<<3,
所以大正方形的边长在2与3之间,
故答案为:2,3.
12.解:∵a,b分别是2021的两个平方根,
∴设a=,则b=﹣,
∴a+b﹣ab
=[+(﹣)]﹣×(﹣)
=0+2021
=2021.
故答案为:2021.
13.解:∵AB∥x轴,点A的坐标为(2,4),并且AB=3,
∴点B的横坐标为:2+3=5或2﹣3=﹣1,纵坐标为4,
∴点B的坐标为(5,4)或(﹣1,4),
故答案为:(5,4)或 (﹣1,4).
14.解:S1=π()2=πAC2,S2=πBC2,
所以S1+S2=π(AC2+BC2)=πAB2=18π.
故答案为:18π.
15.解:设甲提高加工速度后甲加工的零件数y与x之间的函数关系式是y=kx+b,
则,
解得:,
即甲提高加工速度后甲加工的零件数y与x之间的函数关系式是y=30x﹣20(1≤x≤4);
当甲、乙两人相差15个零件时,
①|30x﹣20﹣40|=15,
解得,x1=,x2=;
②30x﹣20﹣60(x﹣3)﹣40=15,
解得,x=,
即当甲、乙两人相差15个零件时,甲加工零件的时间是时或时或时,
故答案为:时或时或时.
16.解:①∵四边形ABCD是正方形,
∴BC=CD,∠BCE=∠DCE=45°.
在△BCE和△DCE中,,
∴△BCE≌△DCE(SAS),
∴∠CBE=∠CDE=15°,故①正确;
②过D作DM⊥AC于M,
∵∠CDE=15°,∠ADC=90°,
∴∠ADE=75°,
∵∠DAE=45°,
∴∠AED=60°,
∵AD=AB=,
∴AM=DM=×=,
∴ME=DM=×=1,
∴AE=+1,故②正确;
③根据勾股定理求出AC=2,
∵DM=,EM=1,
∵∠DCA=45°,∠AED=60°,
∴CM=,
∴CE=CM﹣EM=﹣1,
∴S△DEC=×(﹣1)×=,故③错误;
④在EF上取一点G,使EG=EC,连接CG,
∵BC=CF,
∴∠CBE=∠F,
∴∠CBE=∠CDE=∠F=15°.
∴∠CEG=60°.
∵CE=GE,
∴△CEG是等边三角形.
∴∠CGE=60°,CE=GC,
∴∠GCF=45°,
∴∠ECD=GCF.
在△DEC和△FGC中,,
∴△DEC≌△FGC(SAS),
∴DE=GF.
∵EF=EG+GF,
∴EF=CE+ED,故④正确;
故答案为:①②④.
三.解答题(共72分)
17.解:(1)原式=2+9﹣2
=9;
(2)原式=﹣1+1+﹣+2
=﹣1+1+﹣+2
=+.
18.解:∵x=+1,y=﹣1,
∴x+y=(+1)+(﹣1)=2,xy=(+1)(﹣1)=3﹣1=2,
则x2+3xy+y2
=(x+y)2+xy
=(2)2+2
=12+2
=14.
19.解:(1)如图所示:食堂(﹣4,4)、宿舍楼的位置(﹣5,1)、大门的位置(1,﹣1);
(2)如图所示:办公楼和教学楼的位置即为所求.
20.解:(1)因为一开始油箱剩余100升,也就是油箱的大小,为100升,
行驶一小时后,剩余94升,说明一小时耗油量为100﹣94=6(升);
(2)第小时耗油6升,t小时耗油6t(升),
所以剩余油量为Q=100﹣6t;
(3)当t=12时,Q=100﹣6t=100﹣6×12=8(升).
21.解:(1)着火点C受洒水影响.
理由:如图,过点C作CD⊥AB于D,
由题意知AC=600m,BC=800m,AB=1000m,
∵AC2+BC2=6002+8002=10002,AB2=10002,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,
∴S△ABC=AC•BC=CD•AB,
∴600×800=1000CD,
∴CD=480,
∵飞机中心周围500m以内可以受到洒水影响,
∴着火点C受洒水影响;
(2)当EC=FC=500m时,飞机正好喷到着火点C,
在Rt△CDE中,ED===140(m),
∴EF=280m,
∵飞机的速度为10m/s,
∴280÷10=28(秒),
∵28秒>13秒,
∴着火点C能被扑灭,
答:着火点C能被扑灭.
22.(1)证明:∵BC=6,AD为BC边上的中线,
∴BD=DC=BC=3,
∵AD=4,AB=5,
∴BD2+AD2=AB2,
∴∠ADB=90°,
即AD⊥BC;
(2)解:∵AD⊥BC,AD为BC边上的中线,
∴AB=AC,
∵AB=5,
∴AC=5,
∵△ADC的面积S==,
∴×,
解得:DE=2.4.
23.解:(1)由图象可知:当x=0时,y=60,且轿车比摩托车早出发1小时,
∴轿车的速度=60÷1=60 (千米/小时),
由图象得:摩托车的速度=180÷6=30 (千米/小时),
t=6﹣=1,
故答案是:60,30,1;
(2)设y=kx+b,
把(0,180),(6,0)代入上式得:,
解得:,
∴y=﹣30x+180 (0≤x≤6);
(3)分3种情况:
①两车相遇之前:30x+30+60x+60=180,
解得:x=1;
②两车相遇之后且轿车到甲地之前:30x+60x+60﹣30=180,
解得:x=;
③两车相遇之后且轿车返回途中:30x﹣60(x﹣3)=30,
解得:x=5,
综上所述:摩托车出发后1或或5小时,两车在途中相距30千米.
24.解:(1)①==﹣;
②==﹣;
故答案为:﹣;﹣;
(2)++++…+
=﹣1+﹣+﹣+…+﹣
=﹣1;
(3)﹣+﹣
=﹣+﹣
=﹣+﹣
=
=﹣1.
故答案为:﹣1.
25.解:(1)如图2,作BE⊥AC于点E,在AC的延长线上取点D,使得DE=AE,连接BD,
则BE是AD的垂直平分线,
∴AB=BD,∠A=∠D,
∵3∠A+∠ABC=180°,∠A+∠ABC+∠BCA=180°,
∴∠BCA=2∠A,
∵∠BCA=∠D+∠CBD,
∴∠BCA=∠A+∠CBD=2∠A,
∴∠CBD=∠A,
∴DC=BC=8,
∴AD=DC+AC=8+10=18,
∴AE=AD=9,
∴EC=AD﹣CD=9﹣8=1.
∴在直角△BCE和直角△AEB中,
由勾股定理得到:BC2﹣CE2=AB2﹣AE2,即82﹣12=AB2﹣92,
解得,AB=12,
故答案是:9;12;
(2)作BE⊥AC于点E,在AC的延长线上取点D,使得DE=AE,连接BD,
则BE是边AD的垂直平分线,
∴AB=BD,∠A=∠D.
∵3∠A+2∠B=180°,∠A+∠ABC+∠BCA=180°,
∴2∠A+∠ABC=∠ACB,
∵∠ACB=∠D+∠DBC,
∴2∠A+∠ABC=∠D+∠DBC,
∵∠A=∠D,
∴∠A+∠ABC=∠DBC,BD=AB=c,即∠DCB=∠DBC,
∴DB=DC=c,
由题意得,DE=AE=,
∴EC=AE﹣AC=﹣b=,
在Rt△BEC中,BE2=BC2﹣EC2,
在Rt△BEA中,BE2=BA2﹣EA2,
∴BC2﹣EC2=BA2﹣EA2,即a2﹣()2=c2﹣()2,
整理得,b=.
用电量(千瓦时)
1
2
3
4
5
…
应交电费(元)
0.56
1.12
1.68
2.24
2.80
…
汽车行驶时间t(小时)
0
1
2
3
…
油箱剩余油量Q(升)
100
94
88
82
…
相关试卷
这是一份北师大版(2024)七年级上册数学期中复习第1—2章综合测试卷(含答案解析),共11页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
这是一份北师大版(2024新版)七年级上册数学期中学情评估检测试卷(含答案解析),共11页。试卷主要包含了选择题,填空题,解答题,解答题.等内容,欢迎下载使用。
这是一份人教版(2024新教材)七年级上册数学第1-2章综合测试卷(含答案),共7页。试卷主要包含了﹣57的相反数是,若x的倒数是,则x的值为,下面算法正确的是,如图,比点A表示的数大2的数是,下列语句正确的是,定义关于a,b的新运算等内容,欢迎下载使用。








