高考数学压轴题讲义专题1.2极值点偏移问题利器——极值点偏移判定定理专题练习(原卷版+解析)

这是一份高考数学压轴题讲义专题1.2极值点偏移问题利器——极值点偏移判定定理专题练习(原卷版+解析)，共15页。试卷主要包含了极值点偏移的判定定理，新题展示，对点详析，利器显锋芒，招式演练等内容，欢迎下载使用。
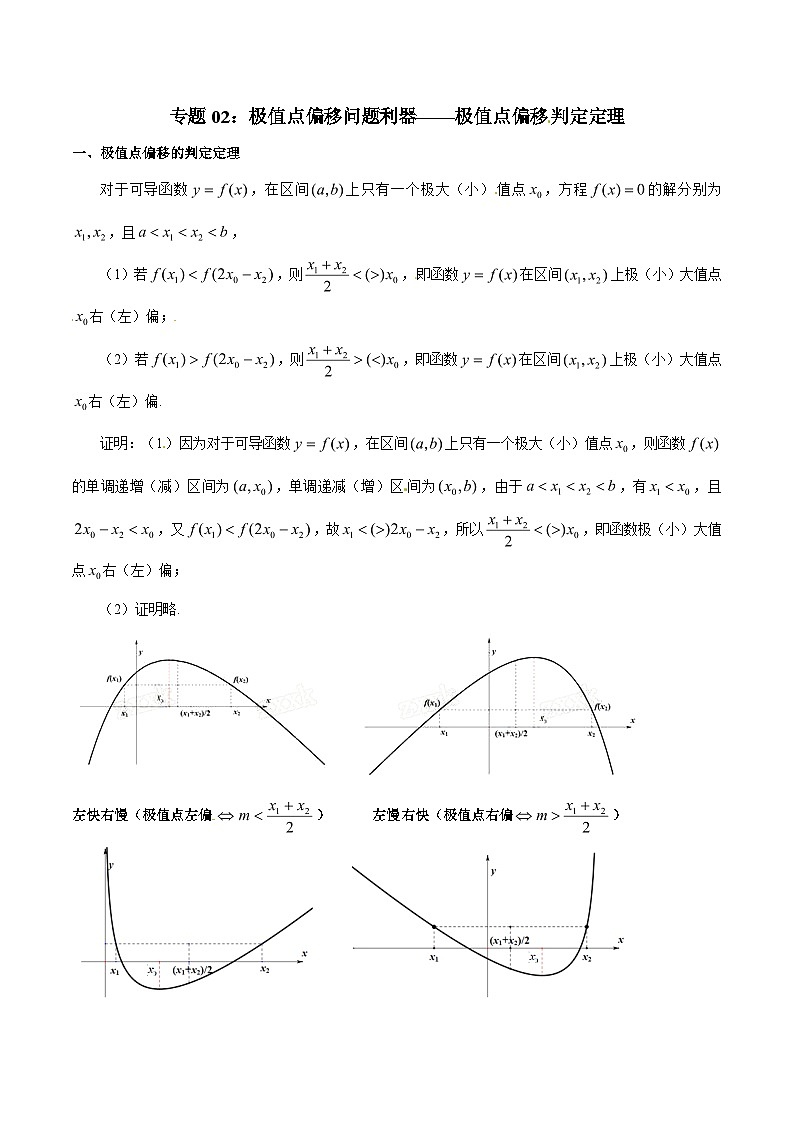
对于可导函数，在区间上只有一个极大（小）值点，方程的解分别为，且，
（1）若，则，即函数在区间上极（小）大值点右（左）偏；
（2）若，则，即函数在区间上极（小）大值点右（左）偏.
证明：（1）因为对于可导函数，在区间上只有一个极大（小）值点，则函数的单调递增（减）区间为，单调递减（增）区间为，由于，有，且，又，故，所以，即函数极（小）大值点右（左）偏；
（2）证明略.
左快右慢（极值点左偏） 左慢右快（极值点右偏）
左快右慢（极值点左偏） 左慢右快（极值点右偏）
二、运用判定定理判定极值点偏移的方法
1、方法概述：
（1）求出函数的极值点；
（2）构造一元差函数；
（3）确定函数的单调性；
（4）结合，判断的符号，从而确定、的大小关系.
口诀：极值偏离对称轴，构造函数觅行踪；四个步骤环相扣，两次单调紧跟随.
2、抽化模型
答题模板：若已知函数满足，为函数的极值点，求证：.
（1）讨论函数的单调性并求出的极值点；
假设此处在上单调递减，在上单调递增.
（2）构造；
注：此处根据题意需要还可以构造成的形式.
（3）通过求导讨论的单调性，判断出在某段区间上的正负，并得出与的大小关系；
假设此处在上单调递增，那么我们便可得出，从而得到：时，.
（4）不妨设，通过的单调性，，与的大小关系得出结论；
接上述情况，由于时，且，，故，又因为，且在上单调递减，从而得到，从而得证.
（5）若要证明，还需进一步讨论与的大小，得出所在的单调区间，从而得出该处函数导数值的正负，从而结论得证.
此处只需继续证明：因为，故，由于在上单调递减，故.[来源:学。科。网]
【说明】
（1）此类试题由于思路固定，所以通常情况下求导比较复杂，计算时须细心；
（2）此类题目若试题难度较低，会分解为三问，前两问分别求的单调性、极值点，证明与（或与）的大小关系；若试题难度较大，则直接给出形如或的结论，让你给予证明，此时自己应主动把该小问分解为三问逐步解题.
三、新题展示
【2019湖南郴州二中月考】已知函数，，．
(1)若，，求函数的单调区间；
(2)设．
(i)若函数有极值，求实数的取值范围；
(ii)若()，求证：．
【2019江西赣州十四县（市)期中联考】已知函数(为常数)，曲线在与轴的交点A处的切线与轴平行．
(1)求的值及函数的单调区间；
(2)若存在不相等的实数使成立，试比较与的大小．
四、对点详析，利器显锋芒
★已知函数.
(1)求函数的单调区间和极值；
(2)若，且，证明：.
★函数与直线交于、两点.
证明：.
★已知函数，若，且，证明：.
★已知函数有两个零点.设是的两个零点，证明：.
五、招式演练
★已知函数，其中为自然对数的底数，是的导函数.
（Ⅰ）求的极值；
（Ⅱ）若，证明：当，且时， .
★已知函数，其中
（1）若函数有两个零点，求的取值范围；
（2）若函数有极大值为，且方程的两根为，且，证明： .
一、极值点偏移的判定定理
对于可导函数，在区间上只有一个极大（小）值点，方程的解分别为，且，
（1）若，则，即函数在区间上极（小）大值点右（左）偏；
（2）若，则，即函数在区间上极（小）大值点右（左）偏.
证明：（1）因为对于可导函数，在区间上只有一个极大（小）值点，则函数的单调递增（减）区间为，单调递减（增）区间为，由于，有，且，又，故，所以，即函数极（小）大值点右（左）偏；
（2）证明略.
左快右慢（极值点左偏） 左慢右快（极值点右偏）
左快右慢（极值点左偏） 左慢右快（极值点右偏）
二、运用判定定理判定极值点偏移的方法
1、方法概述：
（1）求出函数的极值点；
（2）构造一元差函数；
（3）确定函数的单调性；
（4）结合，判断的符号，从而确定、的大小关系.
口诀：极值偏离对称轴，构造函数觅行踪；四个步骤环相扣，两次单调紧跟随.
2、抽化模型
答题模板：若已知函数满足，为函数的极值点，求证：.
（1）讨论函数的单调性并求出的极值点；
假设此处在上单调递减，在上单调递增.
（2）构造；
注：此处根据题意需要还可以构造成的形式.
（3）通过求导讨论的单调性，判断出在某段区间上的正负，并得出与的大小关系；
假设此处在上单调递增，那么我们便可得出，从而得到：时，.
（4）不妨设，通过的单调性，，与的大小关系得出结论；
接上述情况，由于时，且，，故，又因为，且在上单调递减，从而得到，从而得证.
（5）若要证明，还需进一步讨论与的大小，得出所在的单调区间，从而得出该处函数导数值的正负，从而结论得证.
此处只需继续证明：因为，故，由于在上单调递减，故.学科*网
【说明】
（1）此类试题由于思路固定，所以通常情况下求导比较复杂，计算时须细心；
（2）此类题目若试题难度较低，会分解为三问，前两问分别求的单调性、极值点，证明与（或与）的大小关系；若试题难度较大，则直接给出形如或的结论，让你给予证明，此时自己应主动把该小问分解为三问逐步解题.[来源:Z。xx。k.Cm]
三、新题展示
【2019湖南郴州二中月考】已知函数，，．
(1)若，，求函数的单调区间；
(2)设．
(i)若函数有极值，求实数的取值范围；
(ii)若()，求证：．
【答案】（1）见解析；（2）见解析

(2)(i) =，定义域为(0，+∞)，
，
①当时，，函数在(0，+∞)上为单调递增函数，
不存在极值．
②当时，令，得，，
所以，易证在上为增函数，
在上为减函数，所以当时，取得极大值．
所以若函数有极值，实数的取值范围是．
因为，，所以在上为减函数，
，
所以在上为增函数，所以，
即，故成立．
【2019江西赣州十四县（市)期中联考】已知函数(为常数)，曲线在与轴的交点A处的切线与轴平行．
(1)求的值及函数的单调区间；
(2)若存在不相等的实数使成立，试比较与的大小．
【答案】（1）a=2,在区间(－∞，ln 2)上单调递减，在(ln 2，＋∞)上单调递增．（2）x1＋x2＜2ln 2

(2)证明：设x＞ln 2，所以2ln 2－x＜ln 2，
(2ln 2－x)＝e(2ln 2－x)－2(2ln 2－x)－1
＝＋2x－4ln 2－1．
令g(x)＝ (x)－(2ln 2－x)＝ex－－4x＋4ln 2(x≥ln 2)，
所以g′(x)＝ex＋4e－x－4≥0，
当且仅当x＝ln 2时，等号成立，
所以g(x)＝(x)－(2ln 2－x)在(ln 2，＋∞)上单调递增．
又g(ln 2)＝0，所以当x＞ln 2时，g(x)＝(x)－(2ln 2－x)＞g(ln 2)＝0，
即(x)＞(2ln 2－x)，不妨设x1＜ln 2＜x2，所以(x2)＞(2ln 2－x2)，
又因为(x1)＝(x2)，所以(x1)＞(2ln 2－x2)，
由于x2＞ln 2，所以2ln 2－x2＜ln 2，
因为x1＜ln 2，由(1)知函数y＝(x)在区间(－∞，ln 2)上单调递减，
所以x1＜2ln 2－x2，即x1＋x2＜2ln 2．
四、对点详析，利器显锋芒
★已知函数.
(1)求函数的单调区间和极值；
(2)若，且，证明：.
∵，∴，在上单调递增，∴，∴.
★函数与直线交于、两点.
证明：.
★已知函数，若，且，证明：.
【解析】由函数单调性可知：若，则必有，。
所以，
而，
令，则
所以函数在为减函数，所以，
所以即，所以，所以.
★已知函数有两个零点.设是的两个零点，证明：.
五、招式演练
★已知函数，其中为自然对数的底数，是的导函数.
（Ⅰ）求的极值；
（Ⅱ）若，证明：当，且时， .
【答案】(1) 当时， 无极值; 当时, 有极小值;(2)详见解析.
【解析】试题分析：（Ⅰ）求出函数的导数，解关于导函数的不等式，求出函数的单调区间，从而求出函数的极值即可；
（Ⅱ）求出函数f（x）的导数，设函数F（x）=f（x）﹣f（﹣x），求出函数的导数，根据函数的单调性证明即可．
试题解析：
（Ⅰ）的定义域为，
当时， 在时成立
在上单调递增， 无极值.
当时， 解得
由 得；由 得[来源:学。科。网]
所以在上单调递减，在上单调递增，
故有极小值.
（Ⅱ）当时， 的定义域为， ，
由，解得.当变化时， ， 变化情况如下表：
∵，且，则（不妨设）
★已知函数，其中
（1）若函数有两个零点，求的取值范围；
（2）若函数有极大值为，且方程的两根为，且，证明： .
【答案】（1）;（2）见解析.
（1）当时， 函数在上单调递增，不可能有两个零点
（2）当时，
的极大值为，由得；
因为，
所以在必存在一个零点；
显然当时， ，
所以在上必存在一个零点；
[来源:Zxxk.
0
0
+
单调递减
极小值
单调递增
0
-
极大值