新高考数学专题复习专题41概率统计与函数、不等式的综合专题练习(学生版+解析)

这是一份新高考数学专题复习专题41概率统计与函数、不等式的综合专题练习(学生版+解析)，共21页。试卷主要包含了题型选讲，概率与数列的交汇等内容，欢迎下载使用。
一、题型选讲
题型一 、概率与函数的交汇
例1、（2020届浙江省之江教育评价联盟高三第二次联考）设，随机变量的分布列是：
则当在内增大时（ ）
A．增大B．减小C．先增大后减小D．先减小后增大
例2、【2018年高考全国Ⅰ卷理数】某工厂的某种产品成箱包装，每箱200件，每一箱产品在交付用户之前要对产品作检验，如检验出不合格品，则更换为合格品．检验时，先从这箱产品中任取20件作检验，再根据检验结果决定是否对余下的所有产品作检验，设每件产品为不合格品的概率都为，且各件产品是否为不合格品相互独立．
（1）记20件产品中恰有2件不合格品的概率为，求的最大值点．
（2）现对一箱产品检验了20件，结果恰有2件不合格品，以（1）中确定的作为的值．已知每件产品的检验费用为2元，若有不合格品进入用户手中，则工厂要对每件不合格品支付25元的赔偿费用．
（i）若不对该箱余下的产品作检验，这一箱产品的检验费用与赔偿费用的和记为，求；
（ii）以检验费用与赔偿费用和的期望值为决策依据，是否该对这箱余下的所有产品作检验？
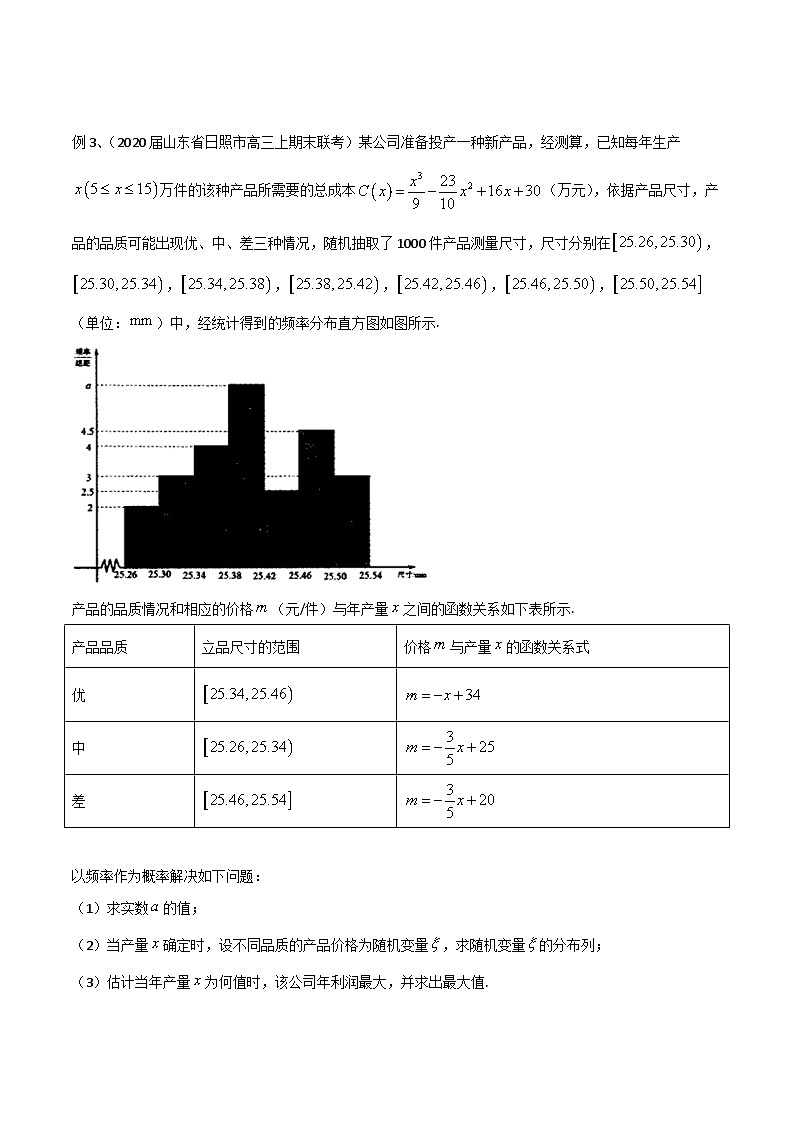
例3、（2020届山东省日照市高三上期末联考）某公司准备投产一种新产品，经测算，已知每年生产万件的该种产品所需要的总成本（万元），依据产品尺寸，产品的品质可能出现优、中、差三种情况，随机抽取了1000件产品测量尺寸，尺寸分别在，，，，，，（单位：）中，经统计得到的频率分布直方图如图所示.
产品的品质情况和相应的价格（元/件）与年产量之间的函数关系如下表所示.
以频率作为概率解决如下问题：
（1）求实数的值；
（2）当产量确定时，设不同品质的产品价格为随机变量，求随机变量的分布列；
（3）估计当年产量为何值时，该公司年利润最大，并求出最大值.
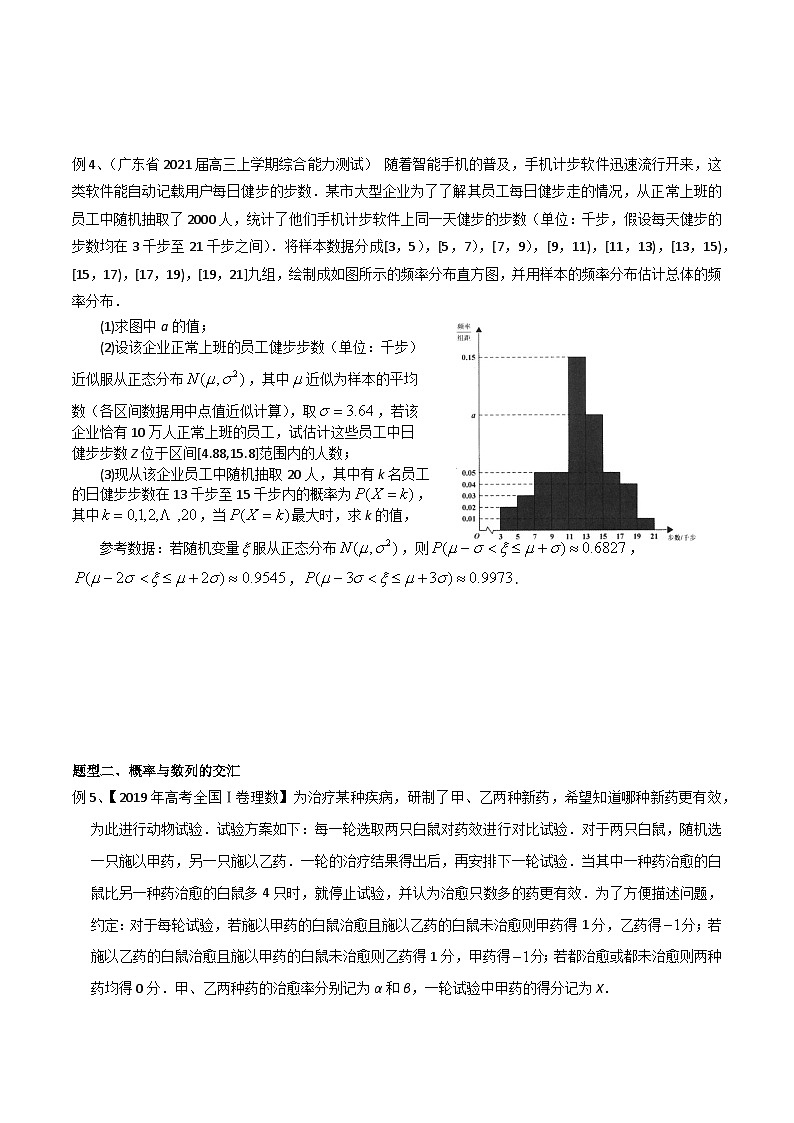
例4、（广东省2021届高三上学期综合能力测试） 随着智能手机的普及，手机计步软件迅速流行开来，这类软件能自动记载用户每日健步的步数．某市大型企业为了了解其员工每日健步走的情况，从正常上班的员工中随机抽取了2000人，统计了他们手机计步软件上同一天健步的步数（单位：千步，假设每天健步的步数均在3千步至21千步之间）．将样本数据分成[3，5），[5，7），[7，9），[9，11)，[11，13)，[13，15)，[15，17)，[17，19)，[19，21]九组，绘制成如图所示的频率分布直方图，并用样本的频率分布估计总体的频率分布．
(1)求图中a的值；
(2)设该企业正常上班的员工健步步数（单位：千步）
近似服从正态分布，其中近似为样本的平均
数（各区间数据用中点值近似计算），取，若该
企业恰有10万人正常上班的员工，试估计这些员工中日
健步步数Z位于区间[4.88,15.8]范围内的人数；
(3)现从该企业员工中随机抽取20人，其中有k名员工
的日健步步数在13千步至15千步内的概率为，
其中，当最大时，求k的值，
参考数据：若随机变量服从正态分布，则，
，.
题型二、概率与数列的交汇
例5、【2019年高考全国Ⅰ卷理数】为治疗某种疾病，研制了甲、乙两种新药，希望知道哪种新药更有效，为此进行动物试验．试验方案如下：每一轮选取两只白鼠对药效进行对比试验．对于两只白鼠，随机选一只施以甲药，另一只施以乙药．一轮的治疗结果得出后，再安排下一轮试验．当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时，就停止试验，并认为治愈只数多的药更有效．为了方便描述问题，约定：对于每轮试验，若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分，乙药得分；若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分，甲药得分；若都治愈或都未治愈则两种药均得0分．甲、乙两种药的治愈率分别记为α和β，一轮试验中甲药的得分记为X．
（1）求的分布列；
（2）若甲药、乙药在试验开始时都赋予4分，表示“甲药的累计得分为时，最终认为甲药比乙药更有效”的概率，则，，，其中，，．假设，．
(i)证明：为等比数列；
(ii)求，并根据的值解释这种试验方案的合理性．
例6、（华南师大附中2021届高三综合测试）足球运动被誉为“世界第一运动”．深受青少年的喜爱．(I)为推广足球运动，某学校成立了足球社团，由于报名人数较多，需对报名者进行“点球测试”来决定是否录取，规则如下：踢点球一次，若踢进，则被录取；若没踢进，则继续踢，直到踢进为止，但是每人最多踢点球3次．
下表是某同学6次的训练数据，以这150个点球中的进球频率代表其单次点球踢进的概率，为加入足球社团，该同学进行了“点球测试”，每次点球是否踢进相互独立，他在测试中所踢的点球次数记为，求的分布列及数学期望；
(II)社团中的甲、乙、丙三名成员将进行传球训练，从甲开始随机地将球传给其他两人中的任意一人，接球者再随机地将球传给其他两人中的任意一人，如此不停地传下去，且假定每次传球都能被接到，记开始传球的人为第1次触球者，第n次触球者是甲的概率记为Pn，即P1 =1．
(i)求P2，P3（直接写出结果即可）；
(ii)证明：数列为等比数列，并判断第19次还是第20次触球者是甲的概率大．
二、达标训练
1、（2020·浙江温州中学高三3月月考）随机变量的可能值有1，2，3，且，，则的最大值为（ ）
A．B．C．D．1
2、（2020届浙江省杭州市第二中学高三3月月考）随机变量的分布列如下：
其中，，成等差数列，则的最大值为（ ）
A．B．C．D．
3、（2020届浙江省杭州市高三3月模拟）已知随机变量ξ满足P (ξ=0) =x，P(ξ=1) =1-x，若则（ ）
A．E(ξ)随着x的增大而增大，D (ξ)随着x的增大而增大
B．E(ξ)随着x的增大而减小，D(ξ)随着x的增大而增大
C．E(ξ)随着x的增大而减小，D(ξ)随着x的增大而减小
D．E(ξ)随着x的增大而增大，D(ξ)随着x的增大而减小
4、（2020届山东省枣庄、滕州市高三上期末）2017年11月河南省三门峡市成功入围“十佳魅力中国城市”，吸引了大批投资商的目光，一些投资商积极准备投入到“魅力城市”的建设之中.某投资公司准备在2018年年初将四百万元投资到三门峡下列两个项目中的一个之中.
项目一：天坑院是黄土高原地域独具特色的民居形式，是人类“穴居”发展史演变的实物见证.现准备投资建设20个天坑院，每个天坑院投资0.2百万元，假设每个天坑院是否盈利是相互独立的，据市场调研，到2020年底每个天坑院盈利的概率为，若盈利则盈利投资额的40%，否则盈利额为0.
项目二：天鹅湖国家湿地公园是一处融生态、文化和人文地理于一体的自然山水景区.据市场调研，投资到该项目上，到2020年底可能盈利投资额的50%，也可能亏损投资额的30%，且这两种情况发生的概率分别为p和.
（1）若投资项目一，记为盈利的天坑院的个数，求（用p表示）；
（2）若投资项目二，记投资项目二的盈利为百万元，求（用p表示）；
（3）在（1）（2）两个条件下，针对以上两个投资项目，请你为投资公司选择一个项目，并说明理由.
5、（2020届山东省潍坊市高三上期中）如图，直角坐标系中，圆的方程为，，，为圆上三个定点，某同学从点开始，用掷骰子的方法移动棋子．规定：①每掷一次骰子，把一枚棋子从一个定点沿圆弧移动到相邻下一个定点；②棋子移动的方向由掷骰子决定，若掷出骰子的点数为偶数，则按图中箭头方向移动；若掷出骰子的点数为奇数，则按图中箭头相反的方向移动．设掷骰子次时，棋子移动到，，处的概率分别为，，．例如：掷骰子一次时，棋子移动到，，处的概率分别为，，．
（1）分别掷骰子二次，三次时，求棋子分别移动到，，处的概率；
（2）掷骰子次时，若以轴非负半轴为始边，以射线，，为终边的角的余弦值记为随机变量，求的分布列和数学期望；
（3）记，，，其中．证明：数列是等比数列，并求.
6、某超市计划按月订购一种酸奶，每天的进货量相同，进货成本为每瓶4元，售价为每瓶6元，未售出的酸奶降价处理，以每瓶2元的价格当天全部处理完.根据往年销售经验，每天需求量与当天最高气温（单位：℃）有关.如果最高气温不低于25，需求量为500瓶；如果最高气温位于区间[20，25），需求量为300瓶；如果最高气温低于20，需求量为200瓶.为了确定六月份的订购计划，统计了前三年六月份各天的最高气温数据，得下面的频数分布表：
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
（1） 求六月份这种酸奶一天的需求量X（单位：瓶）的分布列；
（2） 设六月份一天销售这种酸奶的利润为Y（单位：元）.当六月份这种酸奶一天的进货量n（单位：瓶）为多少时，Y的数学期望达到最大值？
7、甲、乙两人进行围棋比赛，共比赛2n(n∈N*)局，根据以往比赛胜负的情况知，每局甲胜的概率和乙胜的概率均为eq \f(1,2).如果某人获胜的局数多于另一人，则此人赢得比赛．记甲赢得比赛的概率为P(n)．
(1)求P(2)与P(3)的值；
(2)试比较P(n)与P(n＋1)的大小，并证明你的结论．0
1
产品品质
立品尺寸的范围
价格与产量的函数关系式
优
中
差
点球数
20
30
30
25
20
25
进球数
10
17
20
16
13
14
-1
0
1
最高
气温
[10，15）
[15，20）
[20，25）
[25，30）
[30，35）
[35，40）
天数
2
16
36
25
7
4
专题41 概率统计与函数、不等式的综合
一、题型选讲
题型一 、概率与函数的交汇
例1、（2020届浙江省之江教育评价联盟高三第二次联考）设，随机变量的分布列是：
则当在内增大时（ ）
A．增大B．减小C．先增大后减小D．先减小后增大
【答案】A
【解析】根据随机变量的分布列，
则
＝
＝
由于函数的图象为关于的开口方向向下的抛物线，且，函数的对称轴为，
故增大.
例2、【2018年高考全国Ⅰ卷理数】某工厂的某种产品成箱包装，每箱200件，每一箱产品在交付用户之前要对产品作检验，如检验出不合格品，则更换为合格品．检验时，先从这箱产品中任取20件作检验，再根据检验结果决定是否对余下的所有产品作检验，设每件产品为不合格品的概率都为，且各件产品是否为不合格品相互独立．
（1）记20件产品中恰有2件不合格品的概率为，求的最大值点．
（2）现对一箱产品检验了20件，结果恰有2件不合格品，以（1）中确定的作为的值．已知每件产品的检验费用为2元，若有不合格品进入用户手中，则工厂要对每件不合格品支付25元的赔偿费用．
（i）若不对该箱余下的产品作检验，这一箱产品的检验费用与赔偿费用的和记为，求；
（ii）以检验费用与赔偿费用和的期望值为决策依据，是否该对这箱余下的所有产品作检验？
【答案】（1）；（2）（i），（ii）应该对余下的产品作检验．
【解析】（1）20件产品中恰有2件不合格品的概率为．
因此．
令，得，
当时，；当时，．
所以的最大值点为．
（2）由（1）知，．
（i）令表示余下的180件产品中的不合格品件数，
依题意知，，即．
所以．
（ii）如果对余下的产品作检验，则这一箱产品所需要的检验费为400元．
由于，故应该对余下的产品作检验．
例3、（2020届山东省日照市高三上期末联考）某公司准备投产一种新产品，经测算，已知每年生产万件的该种产品所需要的总成本（万元），依据产品尺寸，产品的品质可能出现优、中、差三种情况，随机抽取了1000件产品测量尺寸，尺寸分别在，，，，，，（单位：）中，经统计得到的频率分布直方图如图所示.
产品的品质情况和相应的价格（元/件）与年产量之间的函数关系如下表所示.
以频率作为概率解决如下问题：
（1）求实数的值；
（2）当产量确定时，设不同品质的产品价格为随机变量，求随机变量的分布列；
（3）估计当年产量为何值时，该公司年利润最大，并求出最大值.
【答案】（1）；（2）见解析（3）年产量时，该公司年利润取得最大值，最大利润为138万.
【解析】
（1）由题意得，解得；
（2）当产品品质为优时频率为，此时价格为；
当产品品质为中时频率为，此时价格为；
当产品品质为差时频率为，此时价格为；
以频率作为概率，可得随机变量的分布列为：
（3）设公司年利润为，则
整理得，
显然当时，，时，，
∴当年产量时，取得最大值.
估计当年产量时，该公司年利润取得最大值，最大利润为138万.
例4、（广东省2021届高三上学期综合能力测试） 随着智能手机的普及，手机计步软件迅速流行开来，这类软件能自动记载用户每日健步的步数．某市大型企业为了了解其员工每日健步走的情况，从正常上班的员工中随机抽取了2000人，统计了他们手机计步软件上同一天健步的步数（单位：千步，假设每天健步的步数均在3千步至21千步之间）．将样本数据分成[3，5），[5，7），[7，9），[9，11)，[11，13)，[13，15)，[15，17)，[17，19)，[19，21]九组，绘制成如图所示的频率分布直方图，并用样本的频率分布估计总体的频率分布．
(1)求图中a的值；
(2)设该企业正常上班的员工健步步数（单位：千步）
近似服从正态分布，其中近似为样本的平均
数（各区间数据用中点值近似计算），取，若该
企业恰有10万人正常上班的员工，试估计这些员工中日
健步步数Z位于区间[4.88,15.8]范围内的人数；
(3)现从该企业员工中随机抽取20人，其中有k名员工
的日健步步数在13千步至15千步内的概率为，
其中，当最大时，求k的值，
参考数据：若随机变量服从正态分布，则，
，.
【解析】(1)由，
解得，
(2
，，
则10000×0.8186 = 8186（人），所以日健步步数Z位于区间[4.88,15.8]范围内的人数约为8186人．
(3)设从该企业员工中随机抽取20人日健步步数在13千步至15千步内的员工有X人，则
，其中有k名员工的概率为，其中.
记，
当时，，则；
当时，，则.
所以当时，最大，
题型二、概率与数列的交汇
例5、【2019年高考全国Ⅰ卷理数】为治疗某种疾病，研制了甲、乙两种新药，希望知道哪种新药更有效，为此进行动物试验．试验方案如下：每一轮选取两只白鼠对药效进行对比试验．对于两只白鼠，随机选一只施以甲药，另一只施以乙药．一轮的治疗结果得出后，再安排下一轮试验．当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时，就停止试验，并认为治愈只数多的药更有效．为了方便描述问题，约定：对于每轮试验，若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分，乙药得分；若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分，甲药得分；若都治愈或都未治愈则两种药均得0分．甲、乙两种药的治愈率分别记为α和β，一轮试验中甲药的得分记为X．
（1）求的分布列；
（2）若甲药、乙药在试验开始时都赋予4分，表示“甲药的累计得分为时，最终认为甲药比乙药更有效”的概率，则，，，其中，，．假设，．
(i)证明：为等比数列；
(ii)求，并根据的值解释这种试验方案的合理性．
【答案】（1）分布列见解析；（2）(i)证明见解析，(ii)，解释见解析．
【解析】X的所有可能取值为．
，
，
，
所以的分布列为
（2）（i）由（1）得．
因此，故，
即．
又因为，
所以为公比为4，首项为的等比数列．
（ii）由（i）可得
．
由于，故，
所以．
表示最终认为甲药更有效的概率，
由计算结果可以看出，在甲药治愈率为0.5，乙药治愈率为0.8时，
认为甲药更有效的概率为，
此时得出错误结论的概率非常小，说明这种试验方案合理．
例6、（华南师大附中2021届高三综合测试）足球运动被誉为“世界第一运动”．深受青少年的喜爱．(I)为推广足球运动，某学校成立了足球社团，由于报名人数较多，需对报名者进行“点球测试”来决定是否录取，规则如下：踢点球一次，若踢进，则被录取；若没踢进，则继续踢，直到踢进为止，但是每人最多踢点球3次．
下表是某同学6次的训练数据，以这150个点球中的进球频率代表其单次点球踢进的概率，为加入足球社团，该同学进行了“点球测试”，每次点球是否踢进相互独立，他在测试中所踢的点球次数记为，求的分布列及数学期望；
(II)社团中的甲、乙、丙三名成员将进行传球训练，从甲开始随机地将球传给其他两人中的任意一人，接球者再随机地将球传给其他两人中的任意一人，如此不停地传下去，且假定每次传球都能被接到，记开始传球的人为第1次触球者，第n次触球者是甲的概率记为Pn，即P1 =1．
(i)求P2，P3（直接写出结果即可）；
(ii)证明：数列为等比数列，并判断第19次还是第20次触球者是甲的概率大．
【解析】：(I)这150个点球中的进球频率为，则该同学踢一次点球命中的概率p= 0.6，
由题意，可能取1，2，3，则P（=1）= 0.6，P（=2）= 0.4×0.6=0.24，
P（=3）= 0.4×0.4=0.16，
的分布列为：
即E（）=l×0.6+2×0.24+3×0.16=1.56
(II)(i)由题意P2=0，P3=．
(ii)第n次触球者是甲的概率记为Pn，则当n≥2时，第n-1次触球者是甲的概率为Pn-1，
第n-1次触球者不是甲的概率为1- Pn-1，则，从而，
又是以为首项，公比为的等比数列
则
，故第19次触球者是甲的概率大．
二、达标训练
1、（2020·浙江温州中学高三3月月考）随机变量的可能值有1，2，3，且，，则的最大值为（ ）
A．B．C．D．1
【答案】D
【解析】随机变量的可能值有1，2，3，且，，
可得：，
由，可得
所以．
，
当时，的最大值为1．
故选：D．
2、（2020届浙江省杭州市第二中学高三3月月考）随机变量的分布列如下：
其中，，成等差数列，则的最大值为（ ）
A．B．C．D．
【答案】A
【解析】因为，，成等差数列，
，
.
则的最大值为
3、（2020届浙江省杭州市高三3月模拟）已知随机变量ξ满足P (ξ=0) =x，P(ξ=1) =1-x，若则（ ）
A．E(ξ)随着x的增大而增大，D (ξ)随着x的增大而增大
B．E(ξ)随着x的增大而减小，D(ξ)随着x的增大而增大
C．E(ξ)随着x的增大而减小，D(ξ)随着x的增大而减小
D．E(ξ)随着x的增大而增大，D(ξ)随着x的增大而减小
【答案】B
【解析】依题意，在区间上是减函数.
，注意到函数的开口向下，对称轴为，所以在区间上是增函数，也即在区间上是增函数.
故选：B
4、（2020届山东省枣庄、滕州市高三上期末）2017年11月河南省三门峡市成功入围“十佳魅力中国城市”，吸引了大批投资商的目光，一些投资商积极准备投入到“魅力城市”的建设之中.某投资公司准备在2018年年初将四百万元投资到三门峡下列两个项目中的一个之中.
项目一：天坑院是黄土高原地域独具特色的民居形式，是人类“穴居”发展史演变的实物见证.现准备投资建设20个天坑院，每个天坑院投资0.2百万元，假设每个天坑院是否盈利是相互独立的，据市场调研，到2020年底每个天坑院盈利的概率为，若盈利则盈利投资额的40%，否则盈利额为0.
项目二：天鹅湖国家湿地公园是一处融生态、文化和人文地理于一体的自然山水景区.据市场调研，投资到该项目上，到2020年底可能盈利投资额的50%，也可能亏损投资额的30%，且这两种情况发生的概率分别为p和.
（1）若投资项目一，记为盈利的天坑院的个数，求（用p表示）；
（2）若投资项目二，记投资项目二的盈利为百万元，求（用p表示）；
（3）在（1）（2）两个条件下，针对以上两个投资项目，请你为投资公司选择一个项目，并说明理由.
【答案】（1） （2） （3）见解析
【解析】
（1）解：由题意
则盈利的天坑院数的均值.
（2）若投资项目二，则的分布列为
盈利的均值.
（3）若盈利，则每个天坑院盈利（百万元），
所以投资建设20个天坑院，盈利的均值为
（百万元）.
①当时，，
解得.
.故选择项目一.
②当时，，
解得.
此时选择项一.
③当时，，解得.
此时选择项二.
5、（2020届山东省潍坊市高三上期中）如图，直角坐标系中，圆的方程为，，，为圆上三个定点，某同学从点开始，用掷骰子的方法移动棋子．规定：①每掷一次骰子，把一枚棋子从一个定点沿圆弧移动到相邻下一个定点；②棋子移动的方向由掷骰子决定，若掷出骰子的点数为偶数，则按图中箭头方向移动；若掷出骰子的点数为奇数，则按图中箭头相反的方向移动．设掷骰子次时，棋子移动到，，处的概率分别为，，．例如：掷骰子一次时，棋子移动到，，处的概率分别为，，．
（1）分别掷骰子二次，三次时，求棋子分别移动到，，处的概率；
（2）掷骰子次时，若以轴非负半轴为始边，以射线，，为终边的角的余弦值记为随机变量，求的分布列和数学期望；
（3）记，，，其中．证明：数列是等比数列，并求.
【答案】（1）详见解析；（2）详见解析；（3）证明详见解析，.
【解析】（1），，
，，
综上，
（2）随机变量的可能数值为1，.
综合（1）得
，
，
故随机变量的分布列为
.
（3）易知，因此，
而当时，，
又，
即.
因此，
故
即数列是以为首项，公比为的等比数列.
所以，
又
故.
6、某超市计划按月订购一种酸奶，每天的进货量相同，进货成本为每瓶4元，售价为每瓶6元，未售出的酸奶降价处理，以每瓶2元的价格当天全部处理完.根据往年销售经验，每天需求量与当天最高气温（单位：℃）有关.如果最高气温不低于25，需求量为500瓶；如果最高气温位于区间[20，25），需求量为300瓶；如果最高气温低于20，需求量为200瓶.为了确定六月份的订购计划，统计了前三年六月份各天的最高气温数据，得下面的频数分布表：
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
（1） 求六月份这种酸奶一天的需求量X（单位：瓶）的分布列；
（2） 设六月份一天销售这种酸奶的利润为Y（单位：元）.当六月份这种酸奶一天的进货量n（单位：瓶）为多少时，Y的数学期望达到最大值？
【解析】 （1） 由题意知，X可能取值为200，300，500，
P（X＝200）＝eq \f(2＋16,90)＝0.2，
P（X＝300）＝eq \f(36,90)＝0.4，
P（X＝500）＝eq \f(25＋7＋4,90)＝0.4，
所以X的分布列为
（2） 由题意知，这种酸奶一天的需求量至多为500瓶，至少为200瓶，因此只需考虑200≤n≤500.
当300≤n≤500时，
若最高气温不低于25，则Y＝6n－4n＝2n；
若最高气温位于区间[20，25），
则Y＝6×300＋2（n－300）－4n＝1 200－2n；
若最高气温低于20，
则Y＝6×200＋2（n－200）－4n＝800－2n，
所以E（Y）＝2n×0.4＋（1 200－2n）×0.4＋（800－2n）×0.2＝640－0.4n.
当200≤n1，∴eq \f(Ceq \\al(n,2n),22n)>eq \f(Ceq \\al(n＋1,2n＋2),22n＋2)，
∴P(n)