湘教版（2024）2.6.2菱形的判定习题课件ppt

这是一份湘教版（2024）2.6.2菱形的判定习题课件ppt，共31页。PPT课件主要包含了名师点金，AD∥BC答案不唯等内容，欢迎下载使用。

判定一个四边形是菱形的方法：(1)若已知邻边相等，要证明一个四边形是菱形，有两种方法：①证明四条边都相等；②先证明该四边形是平行四边形，再利用有一组邻边相等的平行四边形是菱形证明.(2)若条件中出现两条对角线，要证明一个四边形是菱形，可考虑利用：①对角线互相垂直且平分的四边形是菱形；②对角线互相垂直的平行四边形是菱形.
知识点1　由边的关系判定菱形
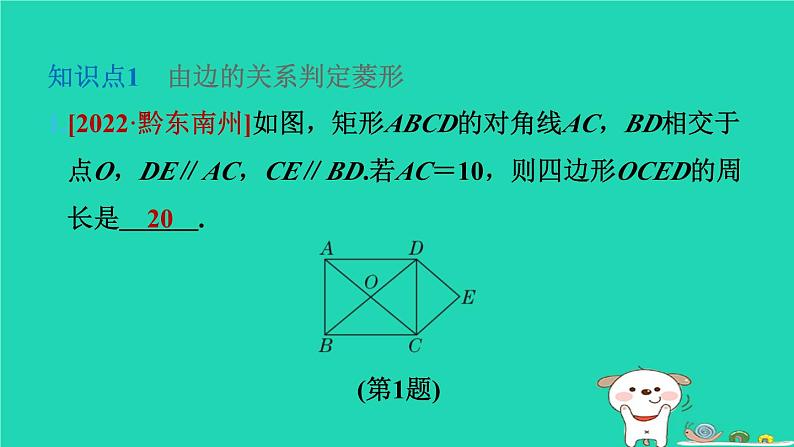
1.[2022·黔东南州]如图，矩形ABCD的对角线AC，BD相交于点O，DE∥AC，CE∥BD.若AC＝10，则四边形OCED的周长是 　20　⁠.
∵DE∥AC，CE∥BD，
∴四边形OCED是平行四边形.
∵矩形ABCD的对角线AC，BD相交于点O，
∴平行四边形OCED是菱形，
∴菱形OCED的周长＝4OC＝4×5＝20.
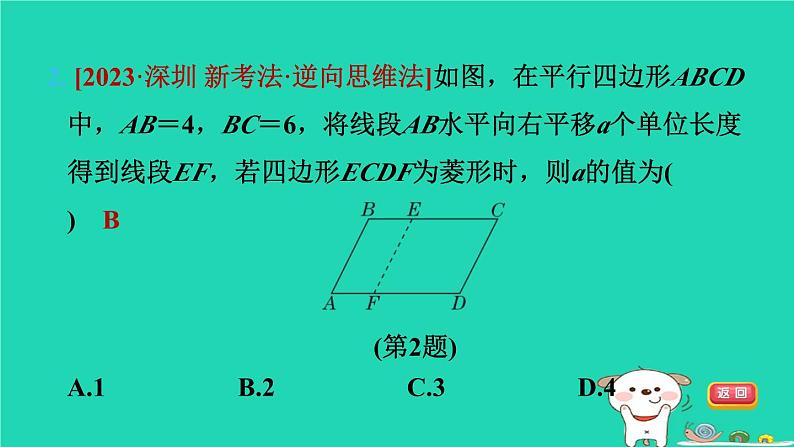
2. [2023·深圳 新考法·逆向思维法]如图，在平行四边形ABCD中，AB＝4，BC＝6，将线段AB水平向右平移a个单位长度得到线段EF，若四边形ECDF为菱形时，则a的值为(　B　)
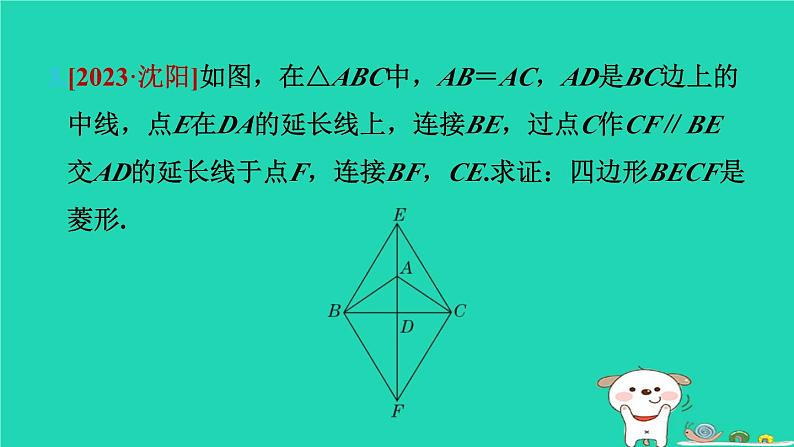
3.[2023·沈阳]如图，在△ABC中，AB＝AC，AD是BC边上的中线，点E在DA的延长线上，连接BE，过点C作CF∥BE交AD的延长线于点F，连接BF，CE.求证：四边形BECF是菱形.
【证明】∵AB＝AC，AD是BC边上的中线，∴AD垂直平分BC，∴EB＝EC，FB＝FC.∵CF∥BE，∴∠BED＝∠CFD，∠EBD＝∠FCD.∵DB＝CD，∴△EBD≌△FCD(AAS)，∴BE＝FC，∴EB＝BF＝FC＝EC，∴四边形EBFC是菱形.
知识点2　由对角线的关系判定菱形4. [2023·嘉兴 新视角·条件开放题]小惠自编一题：“如图，在四边形ABCD中，对角线AC，BD交于点O，AC⊥BD，OB＝OD.求证：四边形ABCD是菱形”，并将自己的证明过程与同学小洁交流.
若赞成小惠的证法，请在第一个框内打“√”；若赞成小洁的说法，请你补充一个条件，并证明.
【解】赞成小洁的说法，补充条件：OA＝OC，证明如下：∵OA＝OC，OB＝OD，∴四边形ABCD是平行四边形.又∵AC⊥BD，∴平行四边形ABCD是菱形.(补充的条件不唯一)
5.[2023·怀化]如图，矩形ABCD中，过对角线BD的中点O作BD的垂线EF，分别交AD，BC于点E，F.(1)求证：△BOF≌△DOE；
【证明】∵四边形ABCD是矩形，∴AD∥BC.∴∠EDO＝∠FBO.∵点O是BD的中点，∴DO＝BO.又∵∠EOD＝∠FOB，∴△BOF≌△DOE(ASA).
(2)连接BE，DF，求证：四边形EBFD是菱形.
【证明】由(1)得△BOF≌△DOE，∴BF＝DE.∵四边形ABCD是矩形，∴AD∥BC，即DE∥BF.∴四边形EBFD是平行四边形.∵EF⊥BD，∴四边形EBFD是菱形.
易错点　臆造菱形的判定方法而出错6.[2023·齐齐哈尔]如图，在四边形ABCD中，AD＝BC，AC⊥BD于点O.请添加一个条件： 　AD∥BC(答案不唯一)　⁠，使四边形ABCD成为菱形.
利用菱形的判定方法判定菱形7.[2023·随州]如图，矩形ABCD的对角线AC，BD相交于点O，DE∥AC，CE∥BD.(1)求证：四边形OCED是菱形；
(2)若BC＝3，DC＝2，求四边形OCED的面积.
利用菱形的性质和判定求平行线间的距离8.[2023·云南]如图，平行四边形ABCD中，AE，CF分别是∠BAD，∠BCD的平分线，且E，F分别在边BC，AD上，AE＝AF.(1)求证：四边形AECF是菱形；
【证明】∵四边形ABCD是平行四边形，∴∠BAD＝∠BCD，AD∥BC.∵AE，CF分别是∠BAD，∠BCD的平分线，
【解】如图，连接AC.
利用勾股定理解菱形的性质和判定的应用9.[2022·广元]如图，在四边形ABCD中，AB∥CD，AC平分∠DAB，AB＝2CD，E为AB的中点，连接CE.(1)求证：四边形AECD为菱形；
【证明】∵E为AB的中点，∴AB＝2AE＝2BE.∵AB＝2CD，∴CD＝AE.又∵AE∥CD，∴四边形AECD是平行四边形.∵AC平分∠DAB，∴∠DAC＝∠EAC.∵AB∥CD，∴∠DCA＝∠EAC.∴∠DCA＝∠DAC.∴AD＝CD.∴四边形AECD是菱形.
(2)若∠D＝120°，DC＝2，求△ABC的面积.
【解】∵四边形AECD是菱形，∠D＝120°，DC＝2，∴AD＝AE＝CE＝DC＝2，∠AEC＝∠D＝120°.∴AE＝CE＝BE＝2，∠CEB＝60°.∴∠CAE＝∠ACE＝30°，△CEB是等边三角形.
利用轴对称性质解菱形的判定和性质的应用10. [新考法 猜想法]如图，在▱ABCD中，BC＝2AB，AB⊥AC，分别在边BC，AD上的点E与点F关于AC对称，连接EF，AE，CF，DE.(1)试判断四边形AECF的形状，并说明理由；
【解】四边形AECF是菱形.理由如下：设AC，EF交于点O，如图.∵四边形ABCD是平行四边形，∴AD∥BC.∴∠OAF＝∠OCE.∵点E与点F关于AC对称，∴AE＝AF，CE＝CF，OE＝OF.
(2)求证：AE⊥DE.