湘教版八年级下册2.6.2菱形的判定优秀ppt课件

导入新课

前面我们学习了矩形和菱形，填表回顾一下知识

回顾前面的内容，积极思考带着问题参与新课.

通过实际情境，让学生感受数学来源于生活，数学知识与生活实践密切相关，增加学生的学习、探索兴趣，便于学生以高昂情绪参与本课的探索过程

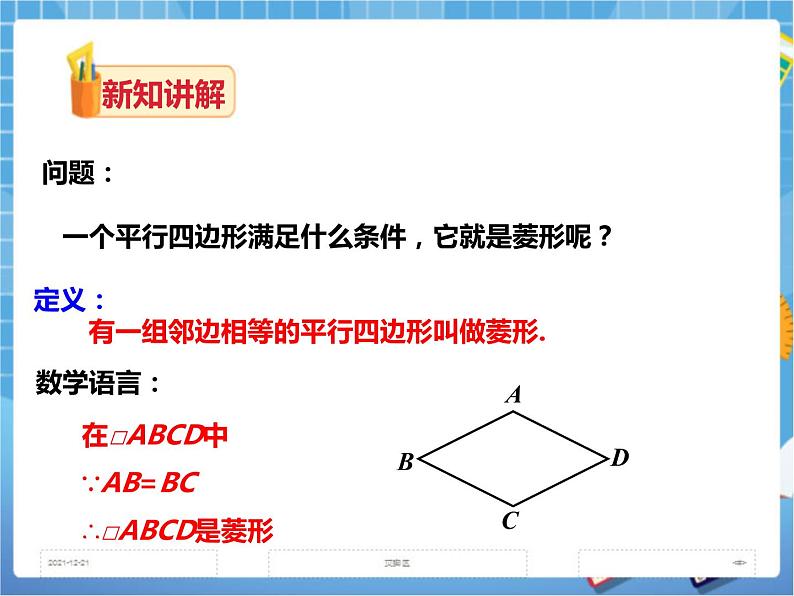
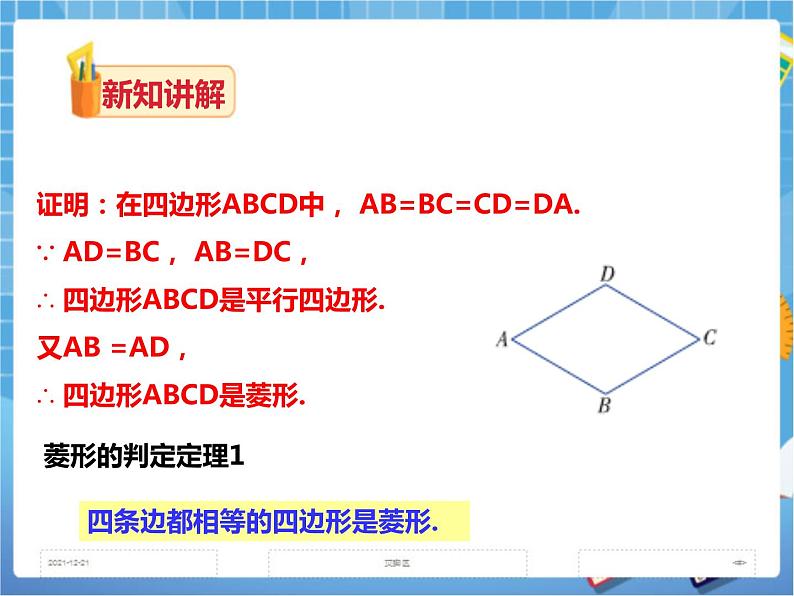
讲授新课

问题：一个平行四边形满足什么条件，它就是菱形呢？

定义：有一组邻边相等的平行四边形叫做菱形.

数学语言：

在□ABCD中 

∵AB=BC

∴□ABCD是菱形

动脑筋

如图，用4支长度相等的铅笔能摆成菱形吗？

把上述问题抽象出来就是：

四条边都相等的四边形是菱形吗？

老师：你能证明吗？

证明：在四边形ABCD中， AB=BC=CD=DA.

∵ AD=BC， AB=DC，

∴ 四边形ABCD是平行四边形.

又AB =AD，

∴ 四边形ABCD是菱形.

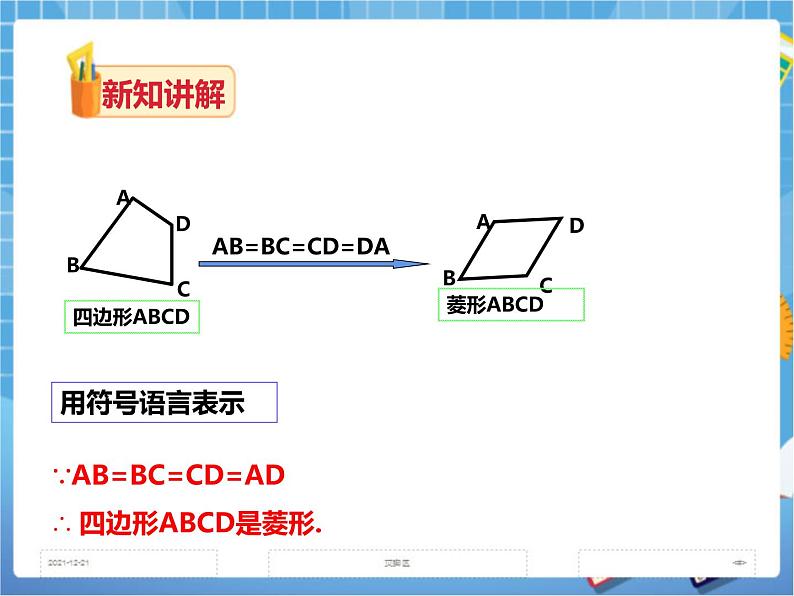
菱形的判定定理1

四条边都相等的四边形是菱形.

用符号语言表示

∵AB=BC=CD=AD

∴ 四边形ABCD是菱形.

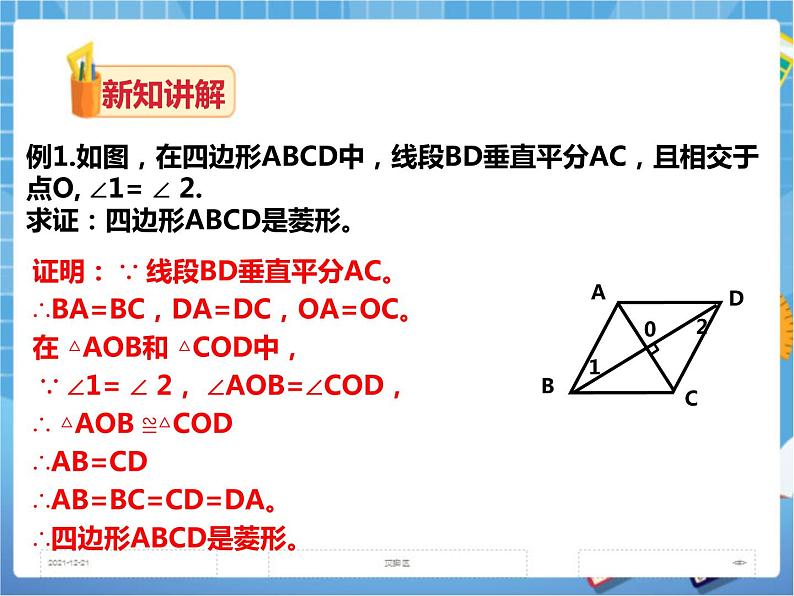
例1.如图，在四边形ABCD中，线段BD垂直平分AC，且相交于点O, ∠1= ∠ 2.

求证：四边形ABCD是菱形。

练一练：

下列命题中正确的是（   ）

    A.一组邻边相等的四边形是菱形

    B.三条边相等的四边形是菱形

    C.四条边相等的四边形是菱形

    D.四个角相等的四边形是菱形

问题：

四边形的对角线满足什么条件，它就是菱形呢？

两条对角线互相垂直的四边形是菱形吗？

不是，四边形可能是“筝形”

动脑筋

菱形的两条对角线互相垂直且平分，从菱形的这一性质受到启发，你能画出一个菱形吗？

学生：过点O画两条互相垂直的线段AC，BD，使

得OA=OC，OB =OD. 连接AB，BC，CD，DA.

则四边形ABCD是菱形

由画法可知，四边形ABCD的两条对角线AC与BD互相平分，因此它是平行四边形. 又已知其对角线互相垂直，上述问题抽象出来就是：

对角线互相垂直的平行四边形是菱形吗？

你能证明吗？

证明：

∵四边形ABCD是平行四边形

∴OA=OC

又∵AC⊥BD;

∴BA=BC

∴□ABCD是菱形。

菱形的判定定理2

对角线互相垂直的平行四边形是菱形．

几何语言：

∵在□ABCD中，AC⊥BD

∴ □ABCD是菱形。

例2.如图，在□ABCD中，AC =6，BD=8，AD=5. 求AB的长.

命题：每条对角线平分一组对角的四边形是菱形.

已知：在四边形ABCD中，AC分别平分∠BAD和∠BCD，BD分别平分∠ABC和∠ADC。求证：四边形ABCD是菱形

注意：这个判定方法不能直接使用

练习：

下列条件中，不能判定四边形ABCD为菱形的是（  ）

A.AC⊥BD,AC与BD互相平分   

B.AB=BC=CD=DA

C.AB=BC,AD=CD,且AC⊥BD    

D.AB=CD,AD=BC,AC⊥BD

总结：

菱形常用的判定方法

1.有一组邻边相等的平行四边形叫做菱形

2.对角线互相垂直的平行四边形是菱形

3.四边都相等的四边形是菱形

利用学生自己手里的工具，激发学生的强烈的好奇心和求知欲。学生经历了将实际问题转化为数学问题的建模过程。

从而得到菱形的判定定理1

在教师的引导下运用菱形的判定定理并启发学生分析，引导学生归纳探究，层层理清命题证明的思路，简化证明方法。 

进一步提出问题，学生进行回答，并举出例子，探究菱形的判定定理2

试着证明菱形的判定定理2，并进行总结。

教师引导学生审题，学生弄清题意后，师生共同分析思路，教师渗透综合分析法。

学生口答，教师板书解题过程。

归纳总结菱形的判定方法

让学生动手动脑，自主发现和认识菱形的判定定理。

培养学生自己读题，理解问题，解决问题的能力。

师生共同完成。引导学生发现问题，提出问题，并能解决问题的能力。

培养学生独立思考，总结归纳的能力。

学生审题是解题的关键，通过运用矩形的性质学会解决简单的实际问题，培养了学生的应用意识。

培养学生自主归纳的能力。

巩固提升

1.如图，四边形ABCD的对角线AC，BD互相垂直，则下列条件能判定四边形ABCD为菱形的条件是(    )

  A.BA=BC           B.AC，BD互相平分     

  C.AC=BD           D.AB∥CD

  答案：B

2.如图，四边形ABCD内有一点E，AE=BE=DE=BC=DC，AB=AD，若∠C=100°，则∠AED的大小是(    )

  A.120°   B.130°   C.140°     D.150°

答案：B

3、如图，已知菱形ABCD的一个内角∠BAD=80°，对角线AC，BD相交于点O，点E在AB上，且BE=BO，则∠EOA=______.

答案： 25°

4.如图，在△ABC中，点D是BC的中点，点E，F分别在线段AD及其延长线上，且DE=DF，给出下列条件：①BE⊥EC；②BF∥CE；③AB=AC，从中选择一个条件使四边形BECF是菱形，你认为这个条件是__________(填序号).

答案：③

5、如图，在四边形ABCD中，AD∥BC，AM⊥BC，垂足为M，AN⊥DC，垂足为N.若∠BAD＝∠BCD，AM＝AN，求证：四边形ABCD是菱形.

答案：

证明：∵AD∥BC，   ∴∠BAD＋∠B＝180°.

∵∠BAD＝∠BCD，   ∴∠BCD＋∠B＝180°.

∴AB∥DC.

∴四边形ABCD是平行四边形.

∴∠B＝∠D.

∵AM＝AN，AM⊥BC，AN⊥DC，

∴Rt△ABM≌Rt△ADN.

∴AB＝AD.

∴平行四边形ABCD是菱形.

学生自主解答，教师讲解答案。

通过这几道题目来反馈学生对本节所学知识的掌握程度，落实基础。学生刚刚接触到新的知识需要一个过程，也就是对新知识从不熟悉到熟练的过程，无论是基础的习题，还是变式强化，都要以学生理解透彻为最终目标。

课堂小结

这节课你有哪些收获？你认为自己的表现如何？

学生归纳本节所学知识

回顾、总结、提高。学生自觉形成本节的课的知识网络

板书

2.6.2菱形的判定

定义：有一组邻边相等的平行四边形叫做菱形.

数学语言：

在□ABCD中 

∵AB=BC

∴□ABCD是菱形