浙江省杭州市上城区建兰中学2024-2025学年九年级上学期月考数学试卷（10月份）

这是一份浙江省杭州市上城区建兰中学2024-2025学年九年级上学期月考数学试卷（10月份），共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．（3分）下列事件中，是必然事件的是（ ）
A．水中捞月B．水涨船高C．守株待兔D．百步穿杨
2．（3分）若二次函数y＝ax2的图象经过点（﹣2．﹣4），则a的值为（ ）
A．﹣2B．2C．﹣1D．1
3．（3分）对于二次函数y＝（x﹣1）2+2的图象，下列说法正确的是（ ）
A．可由y＝﹣x2的图象平移得到
B．对称轴是直线x＝﹣1
C．图象有最低点
D．顶点坐标是（﹣1，2）
4．（3分）我国自古以来就有植树的传统，植树可以净化沙土，防止土地沙漠化，对于调节气候、涵养水源、减轻大气污染具有重要意义．在清明时节植树为最佳，因为此时的气候温暖，适宜树苗的成活．某林业局将一种树苗移植成活的情况绘制成如图统计图，由此可估计这种树苗移植成活的概率约为（ ）
A．0.80B．0.85C．0.90D．0.95
5．（3分）如图，在正方形方格中，A，B，C，D，E，P均在格点处，则点P是下列哪个三角形的外心（ ）
A．△ACEB．△ABDC．△ACDD．△BCE
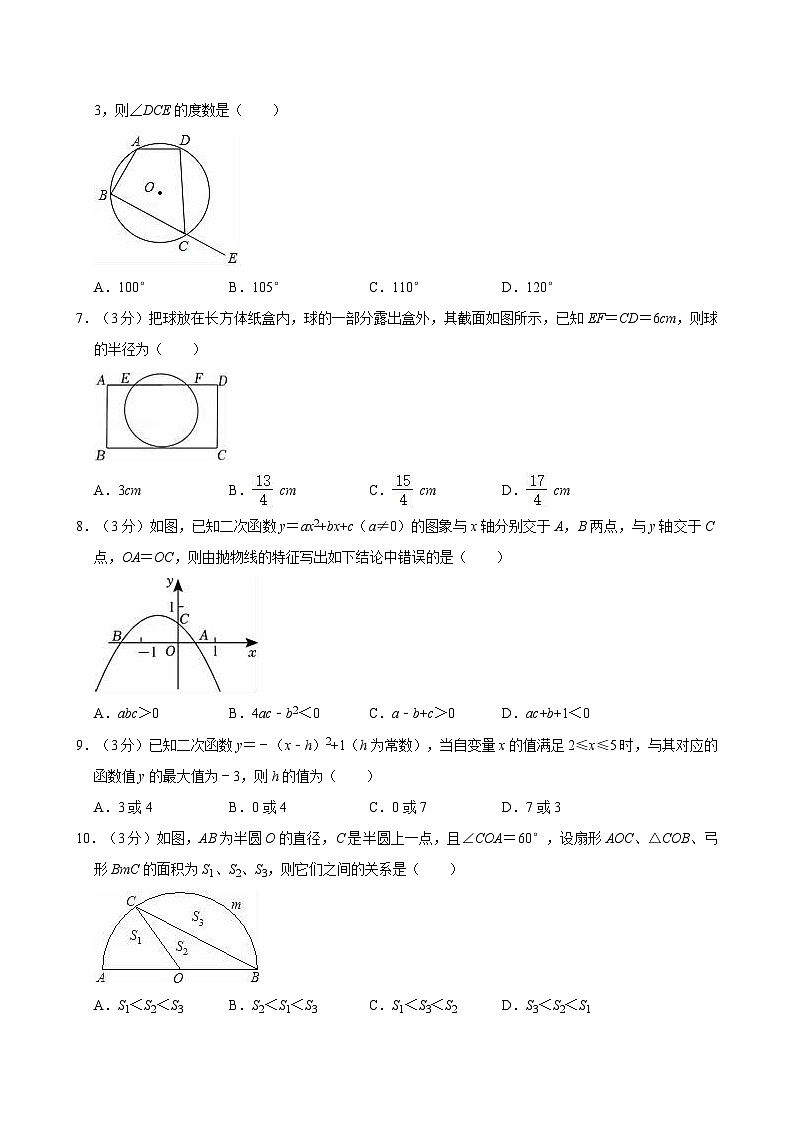
6．（3分）如图，四边形ABCD是⊙O的内接四边形，E在BC的延长线上，若∠A：∠B：∠D＝4：3：3，则∠DCE的度数是（ ）
A．100°B．105°C．110°D．120°
7．（3分）把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知EF＝CD＝6cm，则球的半径为（ ）
A．3cmB． cmC． cmD． cm
8．（3分）如图，已知二次函数y＝ax2+bx+c（a≠0）的图象与x轴分别交于A，B两点，与y轴交于C点，OA＝OC，则由抛物线的特征写出如下结论中错误的是（ ）
A．abc＞0B．4ac﹣b2＜0C．a﹣b+c＞0D．ac+b+1＜0
9．（3分）已知二次函数y＝﹣（x﹣h）2+1（h为常数），当自变量x的值满足2≤x≤5时，与其对应的函数值y的最大值为﹣3，则h的值为（ ）
A．3或4B．0或4C．0或7D．7或3
10．（3分）如图，AB为半圆O的直径，C是半圆上一点，且∠COA＝60°，设扇形AOC、△COB、弓形BmC的面积为S1、S2、S3，则它们之间的关系是（ ）
A．S1＜S2＜S3B．S2＜S1＜S3C．S1＜S3＜S2D．S3＜S2＜S1
二、填空题（每小题3分，共18分）
11．（3分）一个多边形的每个内角均为108°，则这个多边形的边数为 ．
12．（3分）一个不透明的盒子里装有a个除颜色外完全相同的球，其中有6个白球，每次将球充分搅匀后，任意摸出1个球记下颜色然后再放回盒子里，通过如此大量重复试验，发现摸到白球的频率稳定在0.4左右，则a的值约为 ．
13．（3分）如图，直线y1＝mx+n与抛物线相交于点A，B．则关于x的方程mx+n＝a（x+1）2+k的解是 ．
14．（3分）如图，⊙O的半径为1cm，弦AB、CD的长度分别为cm，1cm，则弦AC、BD所夹的锐角α＝ ．
15．（3分）某市民广场有一个直径16米的圆形喷水池，喷水池的周边有一圈喷水头（喷水头高度忽略不计），各方向喷出的水柱恰好在喷水池中心的装饰物OA的顶端A处汇合，水柱离中心3米处达最高5米，如图所示建立直角坐标系．王师傅在喷水池内维修设备期间，喷水管意外喷水，为了不被淋湿，身高1.8米的他站立时必须在离水池中心O 米以内．
16．（3分）如图，MN是⊙O的直径，弦AB∥MN，点C是直径MN上方半圆上的动点（包括端点M，N），∠ACB＝60°，∠ACB和∠CAB的平分线相交于点E，当点C从点M运动到点N时，则C，E两点的运动路径长的比值是 ．
三、解答题（共8体，共72分）
17．（6分）如图是5×5的方格纸，将格点△ABC绕点C按顺时针方向旋转90°．
（1）请画出经旋转后的△A'B'C；
（2）求线段CB在旋转过程中扫过的面积．
18．（6分）如图是等腰△ABC．
（1）以AB为直径求作⊙O，交BC于点D，交AC于点E（要求：尺规作图，不写作法，保留作图痕迹）．
（2）在（1）的条件下，已知AB＝10，CE＝2，求线段BD的长．
19．（8分）从一副普通的扑克牌中取出五张牌，它们的牌面数字分别是4，4，5，5，6．
（1）将这五张扑克牌背面朝上，洗匀后从中随机抽取一张，则抽取的这张牌的牌面数字是4的概率是多少？
（2）将这五张扑克牌背面明上，洗匀后从中随机抽取一张（不放回），再从中随机抽取第二张，请用列表或画树状图的方法，求抽取的这两张牌的牌面数字之和为奇数的概率．
20．（8分）某二次函数图象形状和开口方向与y＝x2相同，且过点A（﹣1，0），B（3，0）．
（1）求该函数的解析式以及顶点坐标；
（2）点P为抛物线上一点，若S△ABP＝24，求出此时点P的坐标．
21．（10分）如图，在给定的圆上依次取点A，B，C，D，连结AB，CD，AC＝BD．设AC，BD交于点E．
（1）求证：AB＝CD．
（2）若弧AD＝100°，AB＝ED，求弧AB的度数．
22．（10分）如图，某农户计划用篱笆围成一个矩形场地养殖家禽，为充分利用现有资源，该矩形场地一面靠墙（墙的长度为18m），另外三面用篱笆围成，中间再用篱笆把它分成三个面积相等的矩形分别养殖不同的家禽，计划购买篱笆的总长度为32m，设矩形场地的长为x m，宽为y m，面积为s m2．
（1）分别求出y与x，s与x的函数解析式；
（2）当x为何值时，矩形场地的总面积最大？最大面积为多少？
（3）若购买的篱笆总长增加8m，矩形场地的最大总面积能否达到100m2？若能，请求出x的值；若不能，请说明理由．
23．（12分）在平面直角坐标系中，抛物线y＝ax2+（a﹣3）x﹣3经过点A（3，t），B（m，p）．
（1）若 t＝0，
①求此抛物线的对称轴；
②当p≥t时，直接写出m的取值范围；
（2）若t＞0，点C（n，q）在该抛物线上，m＞n且m+n＞2，请比较p，q的大小，并说明理由．
24．（12分）已知：点C为⊙O的直径AB上一动点，过点C作CD⊥AB，交⊙O于点D和点E，连接AD、BD，∠DBA的角平分线交⊙O于点F．
（1）若DF＝BD，求证：GD＝GB；
（2）若AB＝2cm，在（1）的条件下，求DG的值；
（3）若∠ADB的角平分线DM交⊙O于点M，交AB于点N．当点C与点O重合时，＝ ；据此猜想，当点C在AB（不含端点）运动过程中，的值是否发生改变？若不变，请求其值；若改变，请说明理由．
2024-2025学年浙江省杭州市上城区建兰中学九年级（上）月考数学试卷（10月份）
参考答案与试题解析
一、选择题（每小题3分，共30分）
1．【解答】解：A、水中捞月是不可能事件，不符合题意；
B、水涨船高是必然事件，符合题意；
C、守株待兔是随机事件，不符合题意；
D、百步穿杨是随机事件，不符合题意．
故选：B．
2．【解答】解：∵二次函数y＝ax2的图象经过点（﹣2，﹣4），
∴代入得：﹣4＝a×（﹣2）2，
解得：a＝﹣1，
故选：C．
3．【解答】解：A、二次函数y＝（x﹣1）2+2的图象可由y＝x2的图象平移得到，故A不符合题意；
B、二次函数y＝（x﹣1）2+2的对称轴为直线x＝1，故B不符合题意；
C、抛物线开口向上，故抛物线有最低点，故C符合题意；
D、二次函数y＝（x﹣1）2+2的顶点坐标为（1，2），故D不符合题意．
故选：C．
4．【解答】解：这种树苗成活的频率稳定在0.9，成活的概率估计值约是0.90．
故选：C．
5．【解答】解：由勾股定理得：PC＝PE＝PB＝＝，
∴P到B、C、E的距离相等，
∴P是△BCE的外心．
故选：D．
6．【解答】解：∵∠A：∠B：∠D＝4：3：3，
∴设∠A＝4x，则∠B＝∠D＝3x．
∵∠B+∠D＝180°，即6x＝180°，解得x＝30°，
∴∠A＝120°，
∵∠A+∠BCD＝180°，∠BCD+∠DCE＝180°，
∴∠DCE＝∠A＝120°．
故选：D．
7．【解答】解：设球的平面投影圆心为O，过点O作ON⊥AD于点N，延长NO交BC于点M，连接OF，如图所示：
则NF＝EN＝EF＝3（cm），
∵四边形ABCD是矩形，
∴∠C＝∠D＝90°，
∴四边形CDNM是矩形，
∴MN＝CD＝6cm，
设OF＝x cm，则OM＝OF，
∴ON＝MN﹣OM＝（6﹣x）cm，
在Rt△ONF中，由勾股定理得：ON2+NF2＝OF2，
即：（6﹣x）2+32＝x2，
解得：x＝，
即球的半径长是cm，
故选：C．
8．【解答】解：由图象可知，a＜0，c＞0，b＜0，
∴abc＞0，
故A正确，不合题意；
由图象与x轴有两个交点可得b2﹣4ac＞0，
故B错误，符合题意；
由图象可知，当x＝﹣1时，y＝a﹣b+c＞0，故C正确，不合题意；
∵OA＝OC，
∴A（c，0），
∴ac2+bc+c＝0，即c（ac+b+1）＝0，
∴c＞0，
∴ac+b+1＝0，故D正确，不合题意．
故选：B．
9．【解答】解：∵函数图象开口方向向下，
∴当x＜h时，y随x增大而增大，当x＞h时，y随x增大而减小，
∴①若h＜2≤x≤5，当x＝2时，y取最大值﹣3，
可得：﹣3＝﹣（2﹣h）2+1，
解得h＝0或4（舍去），
②若2≤x≤5＜h，当x＝5时，y取最大值﹣3，
可得：﹣3＝﹣（5﹣h）2+1，
解得h＝7或3（舍去），
∵2≤h≤5时，y的最大值为1，
∴不符合题意，
综上，h的值为0或7，
故选：C．
10．【解答】解：作OD⊥BC交BC与点D，
∵∠COA＝60°，
∴∠COB＝120°，则∠COD＝60°．
∴S扇形AOC＝；
S扇形BOC＝．
在三角形OCD中，∠OCD＝30°，
∴OD＝，CD＝，BC＝R，
∴S△OBC＝，S弓形＝＝，
＞＞，
∴S2＜S1＜S3．
故选：B．
二、填空题（每小题3分，共18分）
11．【解答】解：180°﹣108°＝72°，
360°÷72°＝5，
故答案为：5．
12．【解答】解：由题意可得，×100%＝0.4，
解得：a＝15．
故答案为：15．
13．【解答】解：∵抛物线y1＝mx+n与抛物线相交于点A（﹣3，0）、B（2，5）两点，
∴方程mx+n＝a（x+1）2+k的两个根为x1＝﹣3，x2＝2，
故答案为：x1＝﹣3，x2＝2．
14．【解答】解：连接OA、OB、OC、OD，
∵OA＝OB＝OC＝OD＝1cm，AB＝cm，CD＝1cm，
∴OA2+OB2＝AB2，OC＝OD＝CD，
∴△AOB是等腰直角三角形，△COD是等边三角形，
∴∠OAB＝∠OBA＝45°，∠ODC＝∠OCD＝60°，
∵∠CDB＝∠CAB，∠ODB＝∠OBD，
∴α＝180°﹣∠CAB﹣∠OBA﹣∠OBD＝180°﹣∠OBA﹣（∠CDB+∠ODB）＝180°﹣45°﹣60°＝75°．
故答案为：75°．
15．【解答】解：设OA右侧的抛物线的解析式为y＝a（x﹣3）2+5，
∵某市民广场有一个直径16米的圆形喷水池，
∴该抛物线过点（8，0），
∴0＝a（8﹣3）2+5，得a＝﹣，
∴OA右侧的抛物线的解析式为y＝﹣（x﹣3）2+5＝x2++，
当y＝1.8时，1.8＝﹣（x﹣3）2+5，得x1＝7，x2＝﹣1，
∵各方向喷出的水柱恰好在喷水池中心的装饰物OA的顶端A处汇合，点A的坐标为（0，），
∴为了不被淋湿，身高1.8米的王师傅站立时必须在离水池中心O7米以内，
故答案为：7．
16．【解答】解：如图1，延长CE交⊙O于点D，连接BD，OD，AD，
由CD平分∠ACB得D恒为劣弧中点．
由已知，得∠5＝∠2＝∠1，∠3＝∠4，
则∠DEA＝∠1+∠3＝∠4+∠5＝∠DAE，
得DA＝DE．
故E在以D为圆心，DA长为半径的圆上．
∵∠ACB＝2∠2＝60°，
∴∠2＝30°，
∴∠BOD＝60°，
∵DO＝BO，
∴△BOD是等边三角形，
∴DO＝DB＝DA，
如图2，当C由M运动到到N时，E运动轨迹为，
C运动路径为与路径对应的圆周半径相同，计算路径长度比即为圆心角之比，
由∠MON＝180°，∠PDQ＝90°得路径长度之比为2：1＝2．
故答案为：2．
三、解答题（共8体，共72分）
17．【解答】解：（1）如图，△A'B'C即为所求．
（2）由勾股定理得，BC＝＝，
∴线段CB在旋转过程中扫过的面积为＝．
18．【解答】解：（1）如图，先作线段AB的垂直平分线，交AB于点O，再以点O为圆心，OA的长为半径画圆，
则⊙O即为所求．
（2）连接BE，AD，
∵AB为⊙O的直径，
∴∠ADB＝90°，∠AEB＝90°．
∵△ABC为等腰三角形，
∴AD为△ABC的中线，AB＝AC＝10，
∴BD＝，AE＝AC﹣CE＝8，
在Rt△ABE中，由勾股定理得，BE＝＝＝6，
在Rt△BCE中，由勾股定理得，BC＝＝＝，
∴BD＝＝．
19．【解答】解：（1）五张牌中，牌面数字分别是4，4，5，5，6，其中牌面数字为4的张数为2，
则P（牌面数字为4）＝；
（2）列表如下：
所有等可能的情况有20种，其中抽取的这两张牌的牌面数字之和为奇数的情况有12种，
则P（抽取的这两张牌的牌面数字之和为奇数）＝＝．
20．【解答】解：（1）根据题意，抛物线解析式为y＝（x+1）（x﹣3），
即y＝x2﹣2x﹣3，
∵y＝x2﹣2x﹣3＝（x﹣1）2﹣4，
∴抛物线的顶点坐标为（1，﹣4）；
（2）设P点坐标为（t，t2﹣2t﹣3），
∵S△ABP＝24，
∴×（3+1）×|t2﹣2t﹣3|＝24，
即|t2﹣2t﹣3|＝12，
解方程t2﹣2t﹣3＝12得t1＝﹣3，t2＝5，
此时P点坐标为（﹣3，12）或（5，12）；
方程t2﹣2t﹣3＝﹣12没有实数解，
综上所述，P点坐标为（﹣3，12）或（5，12）．
21．【解答】（1）证明：∵AC＝BD，
∴＝，
∴＝，
∴AB＝CD；
（2）解：∵弧AD度数的＝100°，
∴∠C＝×100°＝50°，
∵AB＝ED，AB＝CD，
∴CD＝DE，
∴∠DEC＝∠C＝50°，
∴∠D＝180°﹣50°﹣50°＝80°，
∴的度数＝2×80°＝160°，
∵＝，
∴弧AB的度数＝×（360°﹣160°﹣100°）＝50°．
22．【解答】解：（1）由题意得，x+4y＝32，
∴．
∴，即．
（2）由题意，∵，
∴S有最大值．当时，．
答：当x＝16 时，矩形场地的总面积最大，最大面积为64．
（3）由题意得，x+4y＝32+8，
∴．
∴．
∴x1＝x2＝20．
∵18＜20，
∴矩形场地的最大总面积不能达到100m2．
23．【解答】解：（1）①∵t＝0，
∴点A的坐标为（3，0），
将点A坐标代入抛物线函数解析式得，
9a+3（a﹣3）﹣3＝0，
解得a＝1，
∴抛物线的解析式为y＝x2﹣2x﹣3＝（x﹣1）2﹣4，
∴抛物线的对称轴为直线x＝1．
②∵a＝1＞0，
∴抛物线的开口向上，
∴抛物线上的点，离对称轴越近，其函数值越小．
又∵p≥t＝0，
∴|m﹣1|≥3﹣1＝2，
∴m≥3或m≤﹣1．
（2）p＞q．
将点A坐标代入函数解析式得，
t＝9a+3（a﹣3）﹣3＝12a﹣12，
∵t＞0，
∴12a﹣12＞0，
解得a＞1，
∴抛物线的开口向上．
∵抛物线的对称轴为直线x＝，
∴．
∵m＞n，且m+n＞2，
∴m﹣1＞1﹣n，
即点B到对称轴的距离大于点C到对称轴的距离，
∴p＞q．
24．【解答】解：（1）
∵CD⊥直径AB，∴，
∵DF＝BD，
∴，
∴，
∴∠1＝∠2，
∴DG＝BG；
（2）∠DBA的角平分线交⊙O于点F，
∴∠2＝∠3，
由（1）知，∠1＝∠2，
∴∠1＝∠2＝∠3，
∵∠BCD＝90°，
∴∠1+∠2+∠3＝90°，
∴∠1＝∠2＝∠3＝30°，
∵AB是⊙O的直径，
∴∠ADB＝90°，
∴∠4＝90°﹣∠2﹣∠3＝30°，
∵AB＝2，
∴BD＝1，
在Rt△BCD中，∠1＝30°，
∴BC＝BD＝，
在Rt△BCG中，∠3＝30°，
∴CG＝＝，
∴BG＝2CG＝，
由（1）知，DG＝BG＝；
（3）当点C和点O重合时，DM是圆O的直径＝AB，AD＝BD＝AB，
∴＝；
∵∠ADB的角平分线DM交⊙O于点M，交AB于点N，
∴∠ADM＝∠BDM，
∵∠BDM＝∠MAN，
∴∠ADM＝∠MAN，
∵∠AMD＝∠NMA，
∴△MDA∽△MAN，
∴，
∴①
同理得，△MDB∽△MBN，
∴，
∴②，
∵∠ADM＝∠BDM，∠ADB＝90°，
∴∠ABM＝∠BAM＝45°，
∴AM＝BM，AB＝AM
①+②得，，
∴＝＝＝．
4
4
5
5
6
4
﹣﹣﹣
8
9
9
10
4
8
﹣﹣﹣
9
9
10
5
9
9
﹣﹣﹣
10
11
5
9
9
10
﹣﹣﹣
11
6
10
10
11
11
﹣﹣﹣