江西省赣州市南康区2023-2024学年七年级下学期期中考试数学试卷(含答案)
展开1. 化简的结果是( )
A. B. 4C. D. 2
答案:B
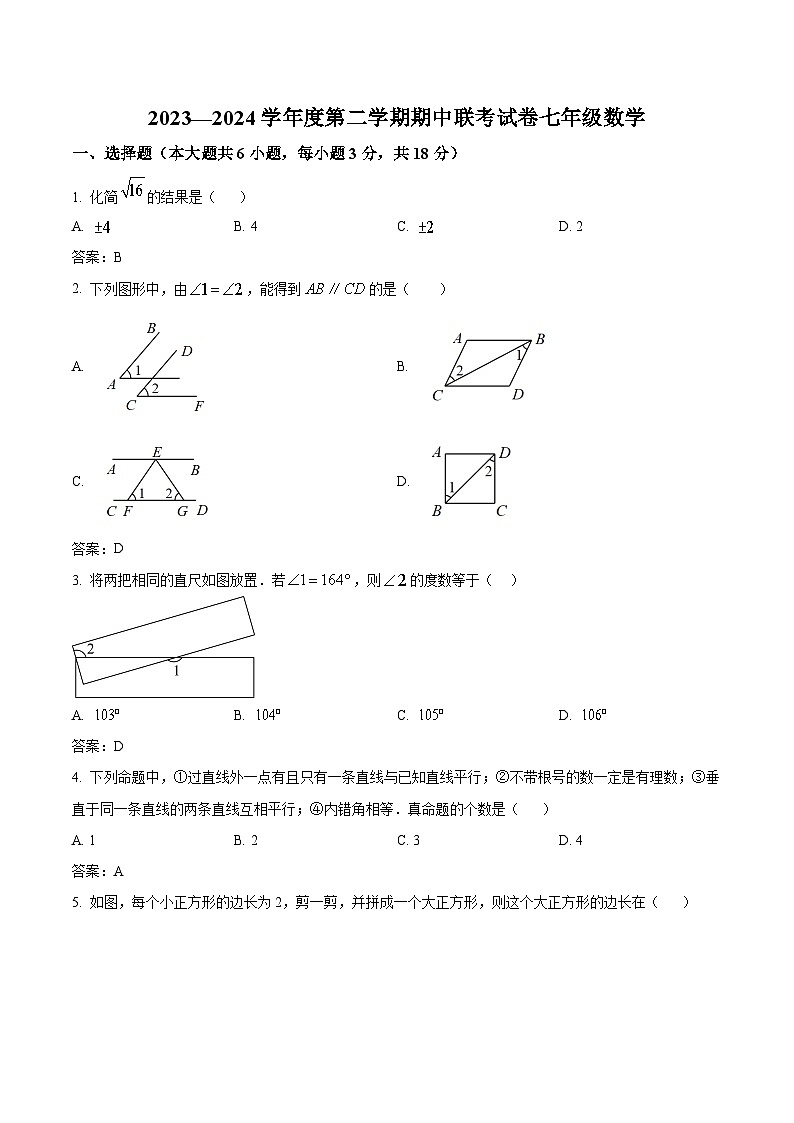
2. 下列图形中,由,能得到的是( )
A. B.
C. D.
答案:D
3. 将两把相同的直尺如图放置.若,则的度数等于( )
A. B. C. D.
答案:D
4. 下列命题中,①过直线外一点有且只有一条直线与已知直线平行;②不带根号的数一定是有理数;③垂直于同一条直线的两条直线互相平行;④内错角相等.真命题的个数是( )
A. 1B. 2C. 3D. 4
答案:A
5. 如图,每个小正方形的边长为2,剪一剪,并拼成一个大正方形,则这个大正方形的边长在( )
A. 2和3之间B. 3和4之间C. 4和5之间D. 5和6之间
答案:C
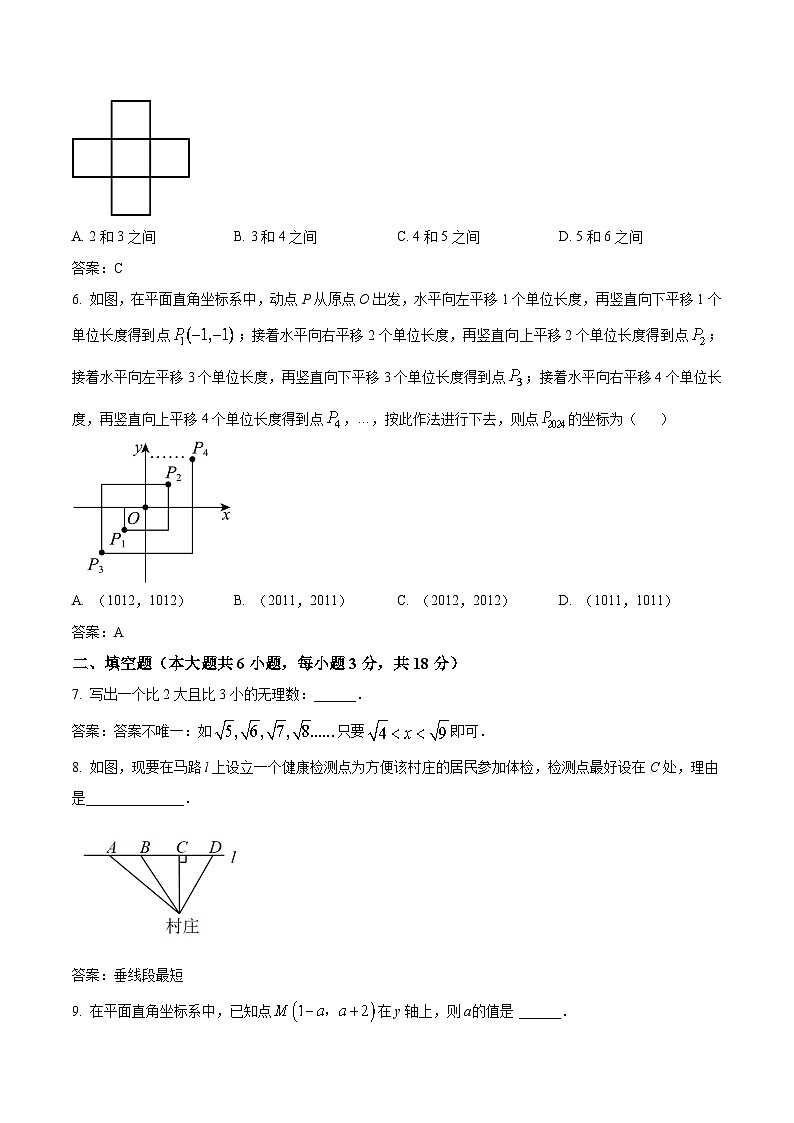
6. 如图,在平面直角坐标系中,动点P从原点O出发,水平向左平移1个单位长度,再竖直向下平移1个单位长度得到点;接着水平向右平移2个单位长度,再竖直向上平移2个单位长度得到点;接着水平向左平移3个单位长度,再竖直向下平移3个单位长度得到点;接着水平向右平移4个单位长度,再竖直向上平移4个单位长度得到点,…,按此作法进行下去,则点的坐标为( )
A. (1012,1012)B. (2011,2011)C. (2012,2012)D. (1011,1011)
答案:A
二、填空题(本大题共6小题,每小题3分,共18分)
7. 写出一个比2大且比3小的无理数:______.
答案:答案不唯一:如只要即可.
8. 如图,现要在马路l上设立一个健康检测点为方便该村庄的居民参加体检,检测点最好设在C处,理由是______________.
答案:垂线段最短
9. 在平面直角坐标系中,已知点在y轴上,则a值是 ______.
答案:1
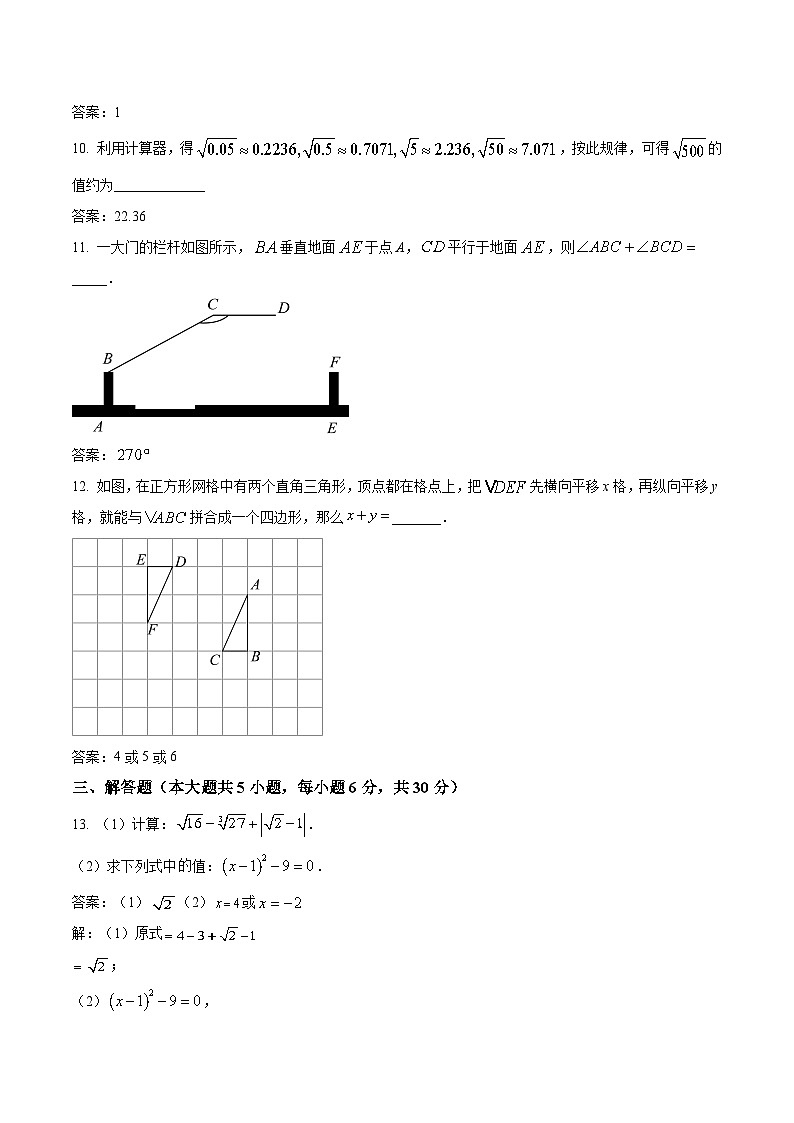
10. 利用计算器,得,按此规律,可得的值约为_____________
答案:22.36
11. 一大门的栏杆如图所示,垂直地面于点A,平行于地面,则_____.
答案:
12. 如图,在正方形网格中有两个直角三角形,顶点都在格点上,把先横向平移x格,再纵向平移y格,就能与拼合成一个四边形,那么_______.
答案:4或5或6
三、解答题(本大题共5小题,每小题6分,共30分)
13. (1)计算:.
(2)求下列式中值:.
答案:(1)(2)或
解:(1)原式
;
(2),
,
∴,
∴或.
14. 已知一个正数的两个平方根分别是和,的相反数为.
(1)求a,b的值;
(2)求的立方根.
答案:(1),
(2)
【小问1详解】
解:一个正数的两个平方根分别是和,的相反数为,
,,
解得:,;
【小问2详解】
,,
,,
的立方方根为.
15. 完成下面的证明:
已知:如图,CD⊥AB,FG⊥AB,垂足分别为D、F,∠1=∠2.
求证:DE∥BC.
证明:∵CD⊥AB,FG⊥AB(已知),
∴∠BDC=∠BFG=90°(垂直的定义),
∴CD∥ ( )
∴∠2=∠3( )
又∵∠1=∠2(已知),
∴∠1=∠3( ),
∴DE∥ ( ).
答案:GF,同位角相等,两直线平行;两直线平行,同位角相等;等量代换;BC,内错角相等,两直线平行
证明:∵CD⊥AB,FG⊥AB(已知),
∴∠BDC=∠BFG=90°(垂直的定义),
∴CD∥GF(同位角相等,两直线平行)
∴∠2=∠3(两直线平行,同位角相等)
又∵∠1=∠2(已知),
∴∠1=∠3(等量代换),
∴DE∥BC(内错角相等,两直线平行).
故答案为:GF,同位角相等,两直线平行;两直线平行,同位角相等;等量代换;BC,内错角相等,两直线平行.
16. 如图,在网格中,每个小正方形边长为1个单位长度,我们把每个小正方形的顶点称为格点;,,均为格点;请按要求仅用一把无刻度的直尺作图.
(1)在图1中,作(在下方),且为格点;
(2)在图2中找一格点(在上方),画出三角形,使得.
答案:(1)见详解 (2)见详解
【小问1详解】
解:如下图所示,即为所求.
【小问2详解】
如下图所示,三角形即为所求.
.
17. 已知点,解答下列各题.
(1)点Q的坐标为,直线轴,求出点P的坐标;
(2)若点P在第二象限,且它到x轴、y轴的距离相等,求的值.
答案:(1)
(2)2025
【小问1详解】
点的坐标为,直线轴,
,
解得:,
,
点的坐标为;
【小问2详解】
点在第二象限,且它到轴、轴的距离相等,
,
解得:,
.
四、(本大题共3小题,每小题8分,共24分)
18. 如图是一种躺椅及其结构示意图,扶手与底座都平行于地面,前支架与后支架分别与交于点G和点D,与交于点N,.
(1)请对说明理由;
(2)若平分,,求扶手与靠背的夹角的度数.
答案:(1)详见解析
(2)
【小问1详解】
理由如下:∵,
∴,
∴;
【小问2详解】
∵与底座都平行于地面,
∴,
∴,
∵,
∴,
∵平分,
∴,
∴,
∵,
∴.
19. 在平面直角坐标系中,给出如下定义:点到轴、轴的距离的较大值称为点的“长距”,点到轴、轴的距离相等时,称点为“完美点”.
(1)点的“长距”为______;
(2)若点是“完美点”,求的值;
(3)若点的长距为4,且点在第二象限内,点的坐标为,试说明:点是“完美点”.
答案:(1)5 (2)1或3
(3)见详解
【小问1详解】
解:根据题意,得点到轴的距离为5,到轴的距离为3,
∴点的“长距”为5.
故答案:5;
【小问2详解】
∵点是“完美点”,
∴,
∴或,
解得或;
【小问3详解】
解:∵点的长距为4,且点在第二象限内,
∴,解得,
∴,
∴点的坐标为,
∴点到轴、轴的距离都是5,
∴点是“完美点”.
20. 某市在招商引资期间,把土地出租给外地某投资商,该投资商为更好地利用土地,将土地的一部分从原来的正方形改建成的长方形,且其长、宽的比为.
(1)求原来正方形场地的周长;
(2)如果把原来正方形场地的铁栅栏围墙全部利用,围成新场地的长方形围墙,那么这些铁栅栏是否够用?试利用所学知识说明理由.
答案:(1)28
(2)够用,理由见详解
【小问1详解】
解:∵原来正方形场地的面积为,
∴原来正方形场地的边长为,
∴原来正方形场地的周长为;
【小问2详解】
解:这些铁栅栏够用,理由如下:
设新长方形场地的长和宽分别为,,
由题意得,
∴(负值舍去),
∴新长方形场地的长和宽分别为,,
∴新长方形场地的周长为,
∵,
∴,
∴这些铁栅栏够用.
五、(本大题共2小题,每小题9分,共18分)
21. 有一个数值转换器.原理如图.
(1)当输入的为25时,输出的______;
(2)是否存在输入有效的值后,始终输不出值?如果存在.请写出所有满足要求的的值;如果不存在,请说明理由;
(3)小明输入数据,在转换器运行程序时,屏幕显示“该操作无法运行”,请你推算输入的数据可能是什么情况?请说明理由;
(4)若输出的是,试判断输入的值是否唯一?若不唯一,请写出其中的3个不同的值.
答案:(1)
(2)0和1 (3)输入的数据可能是负数,理由见详解
(4)3,9,81
【小问1详解】
解:当时,,是无理数,
∴输出的.
故答案为:;
【小问2详解】
当或1时,始终输不出值,
因为0,1的算术平方根是0,1,一定是有理数,
所以,始终输不出值;
【小问3详解】
∵负数没有算术平方根,
∴输入的数据可能是负数;
【小问4详解】
81的算术平方根是9,9的算术平方根是3,3的算术平方根是,
故输入的值不唯一,例如3,9,81.
22. 【学科融合】
射到平面镜上的光线(入射光线)和变向后的光线(反射光线)与平面镜所夹的角相等.如图1,是平面镜,若入射光线与水平镜面夹角为,反射光线与水平镜面夹角为,则.
【应用探究】
有两块平面镜,,入射光线经过两次反射,得到反射光线.
(1)如图2,有两块平面镜,,且,入射光线经过两次反射,得到反射光线.求证.(补充:三角形内角和为)
(2)如图3,光线与相交于点,若,求的度数.
【深入思考】
(3)如图4,有两块平面镜,,且,入射光线经过两次反射,得到反射光线,光线与所在的直线相交于点,,与之间满足的等量关系是______.(直接写出结果)
答案:(1)见详解
(2)
(3)
解析:(1)证明:∵,
∴,
∴,
∵,,
∴,
∴,
∴;
(2)解:∵,
∴,
∵,,
∴,
∴;
(3)∵,
,
,
∴,
∴.
六、(本大题共12分)
23. 如图,在平面直角坐标系中,点,且满足,点从点出发沿轴正方向以每秒2个单位长度的速度匀速移动,点从点出发沿轴负方向以每秒1个单位长度的速度匀速移动.
(1)点的坐标为__________,和位置关系是__________;
(2)当分别是线段上时,连接,使,求出点的坐标;
(3)在的运动过程中,当时,请探究和的数量关系,并说明理由.
答案:(1)
(2)
(3)或,理由见详解
【小问1详解】
解:
故答案为:;
【小问2详解】
过点作于,
设时间经过秒,,则,,
∴
∵
∴,
∵
∴
解得,
∴
∴
∴点的坐标为;
【小问3详解】
解:或,
理由如下:①当点在点的上方时,过点作,如图2所示,
∴
∵
∴
∴
∴
∴,即;
②当点在点的下方时;过点作,如图3所示,
∴
∵
∴
∴
∴
∴
即.
综上所述,或.
2023-2024学年江西省赣州市南康区七年级(下)期中数学试卷(含解析): 这是一份2023-2024学年江西省赣州市南康区七年级(下)期中数学试卷(含解析),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
江西省赣州市南康区2023-2024学年七年级下学期期中数学试题: 这是一份江西省赣州市南康区2023-2024学年七年级下学期期中数学试题,共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
+江西省赣州市南康区2023-2024学年七年级下学期数学期中试卷: 这是一份+江西省赣州市南康区2023-2024学年七年级下学期数学期中试卷,共6页。












