






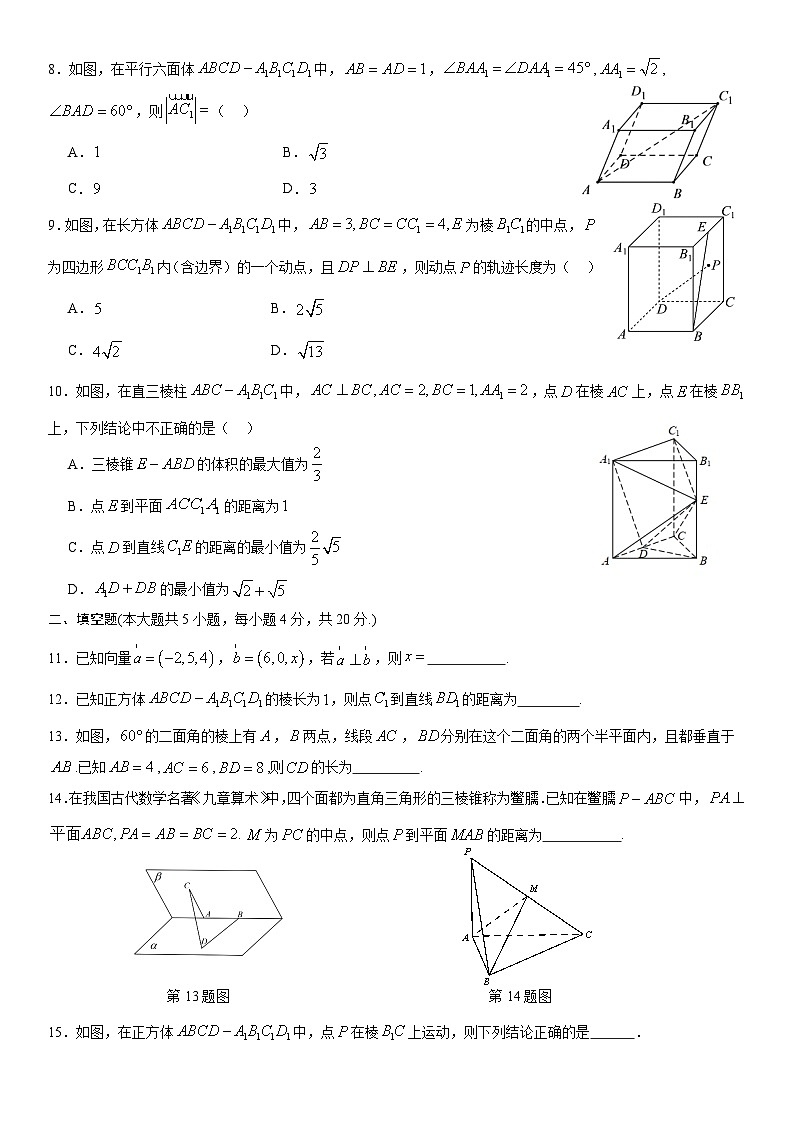

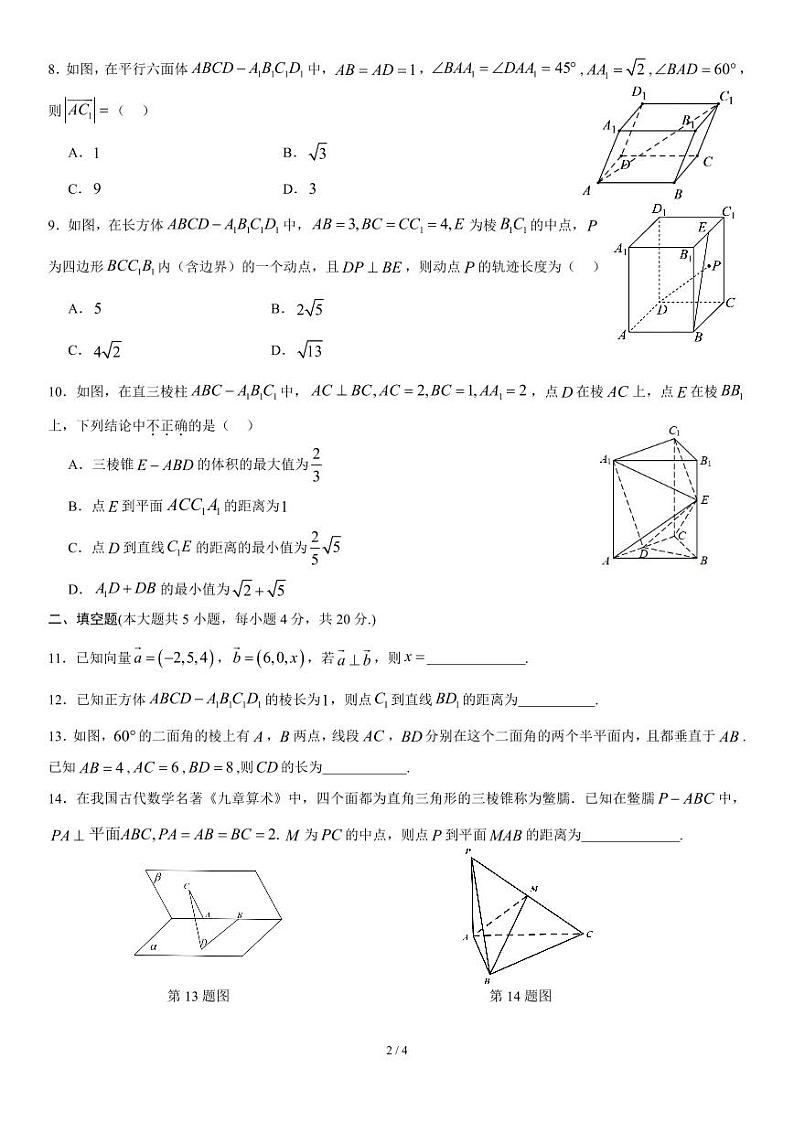
北京市海淀区北京理工大学附属中学2024-2025学年高二上学期10月月考数学试题
展开一、选择题
填空题
3 12. 13. 14. 2 15. ①②④
三、解答题
16.
(1)证明:连接,
∵底面是平行四边形,且是的中点,
∴是的中点,
∵E为PC的中点,
∴,
∵平面,平面,
∴平面.
证明:
∵平面,平面,
∴AB⊥PA,
∵PA⊥AD,AB∩AD=A,AB,AD面ABCD,
∴PA⊥面ABCD,
∵EF//PA,
∴EF⊥面ABCD.
(1)证明:
∵三棱柱是直三棱柱,
∴平面,
∵平面,
∴,
又∵,为中点,
∴,
∵,
∴平面,
∵平面,
∴.
(2)
方法1:
解:∵直三棱柱ABC-A1B1C1,
∴,
∵,
∴,
∵,,
∴,
∵,
∴平面.
∵
∴AB⊥BC,
∵,,
∴平面,
连结,即为直线与平面所成角.
∵,
∴,,
.
∴与平面所成角的正弦值为.
方法2:
解:∵直三棱柱ABC-A1B1C1,
∴,
∵,
∴,
∵,,
∴,
∵,
∴平面.
∵
∴BC⊥AB,
如图所示,以B为原点,以BA,BC,BB1所在直线为x轴,y轴,z轴建立空间直角坐标系B-xyz,
∵A1(2,0,2)C(0,2,0)B(0,0,0),
∴(2,-2,2)(0,2,0),
∵BC⊥面ABB1A1,
∴为平面ABB1A1的一个法向量,
设与平面所成角为θ,
∴,
∴与平面所成角的正弦值为.
(3)解:设A1到平面BEF的距离为d,
∵E(1,1,0),F(0,2,1),A1(2,0,2),
∴,
设为平面BEF的一个法向量,
∴即,
令x=1,则,
,
因此点A1到平面BEF的距离为.
(1)证明:
∵底面是正方形,
∴,
∵平面,平面,
∴平面,
又∵平面与交于点,平面,平面平面
∴.
(2)选条件①②
解:∵侧面为等腰直角三角形,且
∴,,
∵平面平面,平面平面,平面,
∴平面,
∵为正方形,
∴.
以点为坐标原点,以所在直线分别为轴,轴,轴,建立如图所示空间直角坐标系,
则
∵,
∴,
∴BE=,
∴点为的中点,
∴,
∴,
设平面的一个法向量为:,
则,
令,可得,
设平面的法向量为:,则
,,
令,可得,
所以,
则两平面所成的锐二面角为.
选条件①③
∵侧面为等腰直角三角形,且
∴
∵,
∴平面,
∵平面,
∴.
又∵,
∴平面
∵平面
∴
∵,
∴为等腰三角形,
∴点为的中点
又∵,
∴为等腰直角三角形,
下面同①②
选条件②③
∵侧面为等腰直角三角形,且,
∴
∵平面平面,平面平面,平面,
∴平面为正方形,
∴.
又∵,
∴平面,
∵平面
∴
∵,
∴为等腰三角形
∴点为的中点.
下面同①②.
(1)证明:
∵在梯形中,,,,为的中点,∴,,BC=DP,
∴是正三角形,四边形为菱形,
∴,,
∵,
又∵平面ABC,
∴平面ABC,
∵平面,
∴平面⊥平面ABC.
解:
存在.
∵平面,OP⊥AC,
∴,,两两互相垂直,
如图,以点为坐标原点,,,所在直线为,,轴建立空间直角坐标系O-xyz.
则,,,,
∴,,
设平面的一个法向量为,则
,即,令,则,,
,
设,
∵,,
∴,
设与平面所成角为,则,
即,,解得,
∴线段上存在点,且,使得与平面所成角的正弦值为.
题号
1
2
3
4
5
6
7
8
9
10
答案
D
A
C
C
B
D
A
D
B
D
2024-2025学年北京市海淀区北京理工大学附属中学高二上学期回归练习数学试题(含答案): 这是一份2024-2025学年北京市海淀区北京理工大学附属中学高二上学期回归练习数学试题(含答案),共8页。试卷主要包含了选择题,填空题等内容,欢迎下载使用。
2024-2025学年北京市海淀区北京理工大学附属中学高二上学期回归练习数学试题(含解析): 这是一份2024-2025学年北京市海淀区北京理工大学附属中学高二上学期回归练习数学试题(含解析),共13页。试卷主要包含了选择题,填空题等内容,欢迎下载使用。
北京市北京理工大学附属中学2024-2025学年高三上学期开学考试数学练习: 这是一份北京市北京理工大学附属中学2024-2025学年高三上学期开学考试数学练习,共5页。


![[数学]2024~2025学年北京市海淀区北京理工大学附属中学高二上学期开学回归练习试题(有解析)](http://jx-previews-01.oss-cn-hangzhou.aliyuncs.com/3/3/16163525/0-1726382672871/0.jpg?x-oss-process=image/resize,w_202)
![[数学]2024~2025学年北京市海淀区北京理工大学附属中学高二上学期开学回归练习试题(有答案)](http://jx-previews-01.oss-cn-hangzhou.aliyuncs.com/3/3/16163523/0-1726382668287/0.jpg?x-oss-process=image/resize,w_202)








