北师大版（2024）七年级上册（2024）第三章 整式及其加减3 探索与表达规律评课ppt课件

这是一份北师大版（2024）七年级上册（2024）第三章 整式及其加减3 探索与表达规律评课ppt课件，共21页。PPT课件主要包含了学习目标，探索与表达规律，数字和图形中的规律，字母表示数量关系，完成对应练习册等内容，欢迎下载使用。

小亮和好朋友经常玩一种密码游戏:他们事先约定英文字母表中各字母位置的变化规则,以此实现加密和解密。有一次小亮给好朋友留了一张纸条,纸条上写着"kccr zcfglb rfc jgzpypw",好朋友一下子就明白了"meetbehind the library"。问题：小亮他们这次事先约定的宇母位置变化规则是什么?请用代数式表达他们的规则。
今天我们一起进一步探索和表达规律
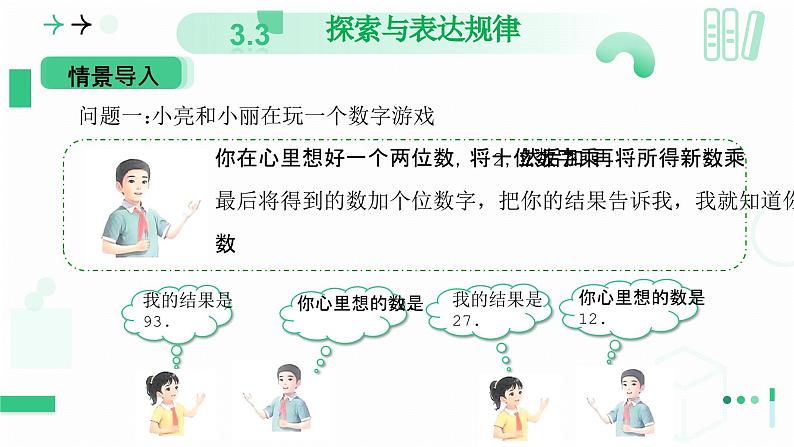
问题一： 小亮和小丽在玩一个数字游戏
问题一：你知道小亮是怎么算出来的吗？
解：设这个两位数的十位数字为a，个位数字为b，则这个两位数表示为10a＋b．则： (2a＋3)×5＋b＝10a＋15＋b=10a+b+15
将所得到结果减去15就是心里想的数．
问题二：设计类似上面的数字游戏，解释其中的道理，并与同伴进行交流.
例如：你在心里想好一个两位数，按照下列步骤进行运算：将十位数字乘5，然后加25，再将所得新数乘2，最后将得到的数加个位数字，把你的结果告诉我，我就知道你心里想的两位数
解：设这个两位数的十位数字为a，个位数字为b，则这个两位数表示为10a＋b．则： (5a＋25)×2＋b＝10a＋50＋b=10a+b+50
将所得到结果减去50就是心里想的数．
例如：随便想一个自然数，将这个数乘5减7，再把结果乘2加14，无论开始想的自然数是什么，按照上面方法计算得到的数的个位数字一定是0.
解：我们可以设任意一个自然数为x，则根据上面的方法可得： 2(5x-7)+14=10x-14+14=10x所以按照上面方法计算得到的数的个位数字一定是0.
问题三：(1)一个三位数能否被3整除,只要看这个数的各数位上的数字之和能否被3整除。你能说明其中的道理吗?
解：设这个三位数的百位数字为a，十位数字为b，个位数字为c则这个三位数表示为100a＋10b+c．按照上面的步骤可得则： 100a＋10b+c＝99a＋9b+（a+b+c)因为99a＋9b一定能被3整除，这个数的各数位上的数字之和能被3整除这个三位数就能被3整除
问题三：(2)一个四位数能否被3整除是否也有这样的规律?请说明理由。
解：设这个四位数的千位数字为a，百位数字为b，十位数字为c，个位数数字为d;则这个四位数表示为1000a＋100b+10c+d．按照上面的步骤可得则： 1000a＋100b+10c+d＝999a＋99b+9c+（a+b+c+d)因为999a＋99b+9c一定能被3整除，这个数的各数位上的数字之和能被3整除这个四位数就能被3整除
问题四：小强和同学玩一个数字游戏小强:"你在心里想好一个数,按照下列步骤进行运算:把这个数乘4,然后加8,再把所得的和乘5,然后再加7,最后再把得到的数乘5。把你的结果告诉我,我就知道你心里想的数了。"同学们试了几次,小强都猜对了。请你解释这是为什么。
解：我们可以设任意这个数为x，则根据上面的方法可得： ［5(4x+8)+7］×5=（20x+47）×5=100x+235所以按照上面方法计算得到的数减去235后除以100就可以.
问题五：观察下列两位数的综合算式:11 x10 -(1+1)=108,12 x10 = (1+2)=117,23×10 - (2 +3)=225,35 x10 = (3 +5) = 342,84 x10 - (8 +4)=828,91 x 10 - (9 +1) =(1)请另外写出一个符合上述规律的算式。(2)运算结果一定是哪个数的倍数?请用字母表示上述观察到的规律。
解：（1）65×10-（6+5）=639
(2)运算结果一定是9的倍数。用字母表示规律为(10a+b)×10-(a+b)=9(11a +b)。
问题五：观察下列两位数的综合算式:11 x10 -(1+1)=108,12 x10 = (1+2)=117,23×10 - (2 +3)=225,35 x10 = (3 +5) = 342,84 x10 - (8 +4)=828,91 x 10 - (9 +1) =(3)运用整式的运算解释上述观察到的规律。
解：(3)(10a+b) x10 - (a+b) = 100a + 10b =a - b = 99a +9b =9 (11a + b)。所以运算结果一定是9的倍数。
问题五：观察下列两位数的综合算式:(4)三位数是否有类似的结论?若有,请用字母表示出来;若没有,请举例说明。(只写答案即可)
(4)三位数有类似的结论。理由如下:设三位数的百位数字为a,十位数字为b,个位数字为c,则该三位数(100a+10b+c)因为(100a+10b+c)×10-(a+b+c)=1 000a +100b +10c-a-b-c=999a+99b+9c =9(111a+11b+c),所以能被9整除,即三位数有类似的结论。
问题六：现在你能解决密码游戏了吗？
解：kccr zcfglb rfc jgzpypw到meet behind the library"。(1)小亮他们这次事先约定的字母位置变化规则是，每个字母换成字母表中其后的第2个字母.设原字母位置为第2个,则实际位置换成字母表中第(x+2)个.
（2）也可事先约定的字母位置变化规则是把每个字母换成字母表中其后的第1个字母(答案不唯一)。
问题四：回顾本章的学习,在用字母表达数量关系和运算方面你积累了哪些经验?
（1）简化数学表达（2）在推导和证明过程中，使用字母可以避免具体数值的干扰，使推理过程更加清晰和一般化（3）使用字母可以帮助明确不同数量之间的关系，使得数学关系更加清晰（4）字母表示法使得数学公式和定理容易推广到更一般的情况。
1,末两位是00,25,50,75的任何数均能被25整除,这是为什么?请解释其中的道理。
解5.解:设一个数末两位为b,其他位数为a,则这个数可表示为100a+b。00,25,50,75均能被25整除,故b能被25整除。又因为25能整除100a,所以100a+b能被25整除。故末两位是00,25,50,75的任何数均能被25整除。
2. 32024的个位数字是多少?
解,32=9,33=27,34=81,35=243,36=729, 37 = 2187, 38=6561, 的正整数次幂的个位数字依次以3,9,7,1循环出现,2024÷4=506,所以32024的个位数字是1.
3.(1)观察下面图中小圆圆的排列方式,你发现了什么规律?(2)根据(1)中的规律猜想:1+3+5+7+..+99(3)一般地,你能得到什么猜想?请用代数式表示。
解：(1)第n个图中小圆圈的个数为n2。(2)502因为:由1+3=22,1+3+5=32,1+3+5+7 =42,1+3+5+7+9=52, 得1+3+5+7+...+99=502。(3)1+3+5+7+...+(2n-1)= n2。
使用字母可以避免具体数值的干扰，使推理过程更加清晰和一般化
找出序号n与数字的对应关系
基础作业：课本P98-99页随堂练习