初中数学北师大版（2024）七年级上册（2024）3 探索与表达规律背景图课件ppt

这是一份初中数学北师大版（2024）七年级上册（2024）3 探索与表达规律背景图课件ppt，共51页。PPT课件主要包含了课堂导入，a-1，a+1，a-7，a+7，a-8，a-6，a+6，a+8，纵列相邻两数相差7等内容，欢迎下载使用。

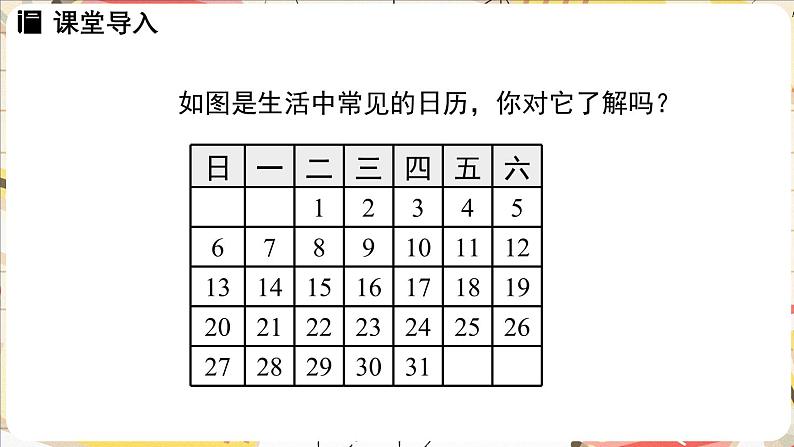
如图是生活中常见的日历，你对它了解吗？
知识点 日历中的数学规律
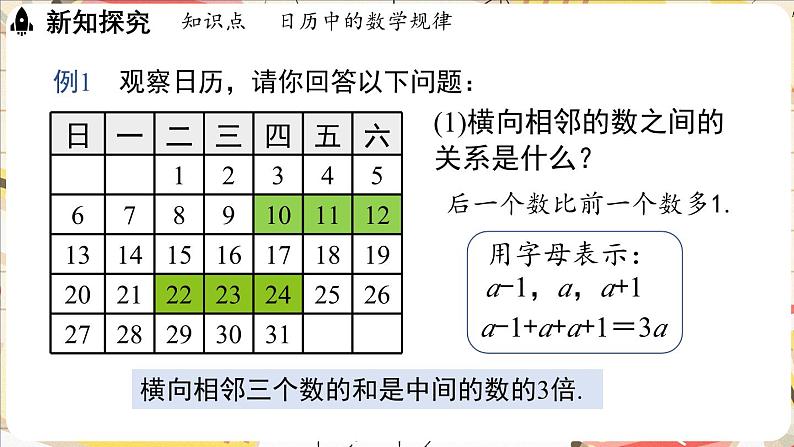
(1)横向相邻的数之间的关系是什么？
后一个数比前一个数多1.
用字母表示：a-1，a，a+1
a-1+a+a+1＝3a
横向相邻三个数的和是中间的数的3倍.
例1 观察日历，请你回答以下问题：
(2)纵向相邻的数之间的关系是什么？
下边一个数比上边一个数多7.
用字母表示：a-7，a，a+7
a-7+a+a+7＝3a
纵向相邻三个数的和是中间的数的3倍.
(3)斜下方三个相邻的数之间的关系是什么？
用字母表示：a-8，a，a+8
a-8+a+a+8＝3a
斜下方三个相邻数的和是中间的数的3倍.
右下一个数比左上一个数多8.
(4)斜上方三个相邻的数之间的关系是什么？
左下一个数比右上一个数多6.
用字母表示：a+6，a，a-6
a+6+a+a-6＝3a
斜上方三个相邻数的和是中间的数的3倍.
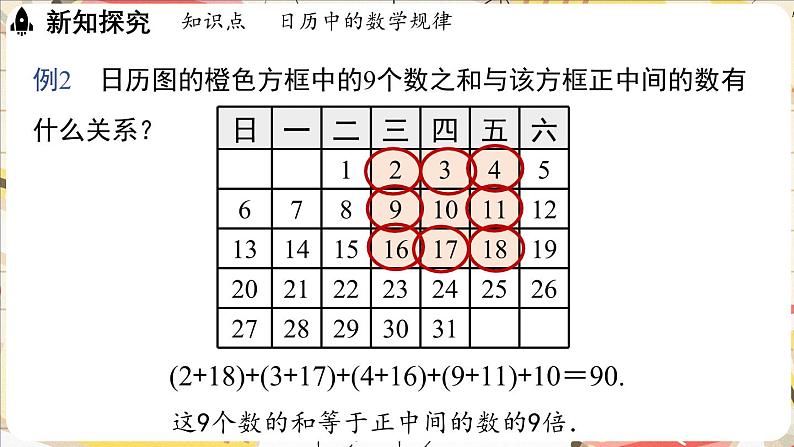
例2 日历图的橙色方框中的9个数之和与该方框正中间的数有什么关系？
(2+18)+(3+17)+(4+16)+(9+11)+10＝90.
这9个数的和等于正中间的数的9倍．
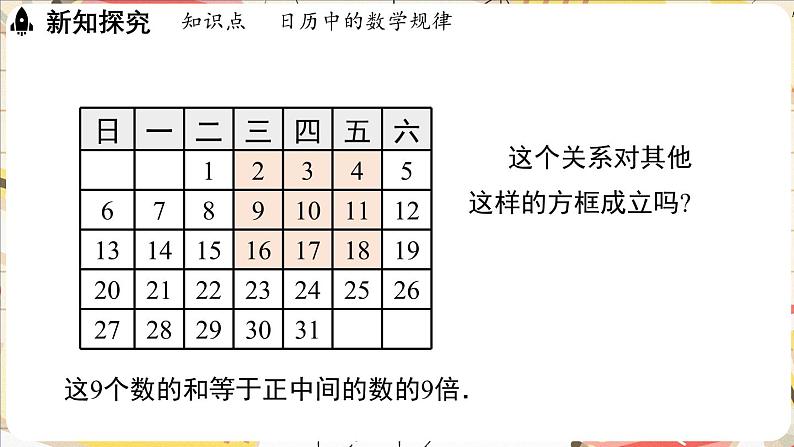
这个关系对其他这样的方框成立吗?
(a-8)+(a-7)+(a-6)+(a-1)+a+(a+1)+(a+6)+(a+7)+(a+8) ＝ ____.
规律：方框中九个数之和＝9×正中间的数．
归纳：
如果用a表示正中间的数，这9个数的和等于9a．
任意一行或列的相邻三个数的和等于最中间的数的3倍.如果设最中间的数为a，则任意一行或列的相邻三个数的和为3a.
思考1：能否使方框中9个数的和为144? 180呢?
解：假设方框正中间的数为a，框中9个数的和为9a.使得9a=144，所以a=16.在图中能找到这样的方框，所以能使框中9个数的和为144.
当9a=180时，a=20.在图中不能找到这样的方框，所以不能使框中9个数的和为180.
思考2：在某个月的日历中，恰好有五个星期日位于同一列且日期数的和为80，这个月的第一个星期日是几号?
解：假设这个月的第一个星期日是m号，则m+(m+7)+(m+7+7)+(m+7+7+7)+(m+7+7+7+7)=80，所以m=2，所以这个月的第一个星期日是2号.
思考3：如果将方框改为十字形框，你能发现哪些规律？
7+13+14+15+21＝70
十字形框中5个数的和等于正中间的数的5倍．
思考4：如果将方框改为H形框，你能发现哪些规律？
10+12+17+18+19+24+26＝126
H形框中7个数的和等于正中间的数的7倍．
思考5：你还能设计其它形状的包含数字规律的数框吗？
8+10+16+22+24＝80
X形框中5个数的和等于正中间的数的5倍．
1.观察如图所示的日历，解答问题：
用一个方框去框图中的4个数(如图中阴影框所示)，若最小的数为x，则其他三个数由小到大分别为 　 x ，＋ 7， 　 x .
2.图1是生活中常见的日历，先观察，再解答：
(1)图2是另一个月的日历，a表示该月中某一天，b，c，d是该月中其他3天，则b，c，d与a的关系：b＝______，c＝______，d＝______．(用含a的式子填空)
图1 图2
(2)用一个长方形框框出日历中的三个数(图3中的阴影)，如果这三个数的和等于51，那么这三个数各是多少？
解：设中间的数为x，则上面的数为x－7，下面的数为x＋7.根据题意，得(x－7)＋x＋(x＋7)＝51，所以x＝17. 所以这三个数分别是10，17，24.
1 3 5 7 911 13 15 17 1921 23 25 27 2931 33 35 37 37
3.将连续的奇数1，3，5，7，9，…排成如图所示的数表.(1)十字形框中的五个数之和与中间数15有什么关系？
答：十字形框中的五个数之和是中间数15的5倍.
解：5+25+13+17+15＝75
(2)设中间数为a，如何用代数式表示十字形框中五个数之和？
解：十字形框中的五个数分别为a，a-10，a-2，a+2，a+10，a+a-10+a-2+a+2+a+10=5a，它们的和是5a.
解：十字形框中的五数之和一定是5的倍数.而2022不是5的倍数，所以十字形框中的五数之和不能等于2022.十字形框中的五数之和能等于2025，此时中间数为405，其余四个数分别为395 ,403 ,407 ,415.
(3)十字形框中的五数之和能等于2022吗？能等于2025吗？
在日历中，方框中的9个数之和是最中间数的9倍.如果用a表示正中间的数，这9个数的和等于9a.任意一行或列的相邻三个数的和等于最中间数的3倍.设最中间的数为a，则任意一行或列的相邻三个数的和为3a.
3.3 探索与表达规律
小明：你在心里想好一个两位数，将十位数字乘2，然后加3，再将所得的和乘5，最后将得到的数加你想的那个两位数的个位数字.把你的结果告诉我，我就知道你心里想的两位数.
你知道小明是怎么算出来的吗?
得到的结果比原两位数大15.
如果用a，b分别表示一个两位数的十位数字和个位数字，那么这个两位数可以表示为________ .
=10a+b+15
知识点1 数与式的变化规律
① ② ③ ④ ⑤ 第n个数
若是分数，则可分别观察分子、分母的变化规律及它们之间的联系.
若是等式，则可将每个等式对应写好，然后比较每一行、每一列数字之间的关系，从而找出规律.
归纳： 数与式的规律问题:从给定的几个数与式入手，观察数与数之间的规律及式子本身存在的规律，分别进行横向、纵向的比较，找出其中的不变部分与变化部分，确定数和式子与序号之间的关系，找出变化规律.
归纳： 数与式的规律问题:若是一列整数，则可考虑相邻两数的和、差、积、商等方面的规律，也可以是奇、偶、平方等方面的规律；若是等式，则可将每个等式对应写好，然后比较每一行、每一列数字之间的关系，从而找出规律；若是分数，则可分别观察分子、分母的变化规律及它们之间的联系．
例3 如图，填在各方格中的三个数之间都具有相同的规律，根据此规律，n的值是（　C　）
知识点2 图形的变化规律
例4 按如图方式摆放餐桌和椅子，回答下列问题：（1）1张餐桌可坐6人，2张餐桌可坐多少人？（2）按照图中的方式继续排列餐桌，完成下表：
方法一 因为每增加一张桌子，就可多坐4个人，所以摆n张桌子可坐：[6＋4(n－1)]个人．即6＋4(n－1)＝4n＋2．
（3）摆n张桌子时可坐多少？用代数式表示；
方法二 每张桌子的两侧各坐2人共4人，n张桌子可坐4n人，再加上两头可坐的两人，共(4n＋2)人．
方法三 每张桌子的一侧可坐2人，n张桌子的一侧可坐2n人，另一侧也可坐2n人，再加上两头各1人，共2n＋2n＋2＝（4n＋2）(人)．
照此规律搭下去，回答下列问题：（1）搭 8个这样的三角形需要多少根火柴棒？
3+(8﹣1)×2=17.
例5 用火柴棒按如图的方式搭三角形：
3×8﹣(8﹣1)=17.
解：3+(n﹣1)×2=2n+1 (或3n﹣(n﹣1)=2n+1).答：搭n个这样的三角形需要(2n+1)根火柴棒.
照此规律搭下去，回答下列问题：（2）搭 n个这样的三角形需要多少根火柴棒？
归纳：图形的变化规律问题: 观察、分析图形特点，挖掘相邻两个图形间的增减变化关系，有时也可将图形进行分割，从不同角度分析图形的变化特点，从中找出规律，大胆猜想，用恰当的代数式表示规律并加以验证.
2.如图，填在各正方形中的四个数之间都有相同的规律，根据此规律，m的值是（　D　）
3.下列是按一定规律排列的单项式：x，－2x2，3x3，－4x4，5x5，－6x6，…，第n个单项式是（　C　）
4.观察如图所示的“蜂窝图”．  则第n个图案中的“ ”的个数是________.(用含有n的代数式表示)．
5.观察下列图形，则第n个图形中三角形的个数是(　　) A．2n＋2　　 B．4n＋4　 　C．4n－4　　 D．4n
探究规律的一般步骤(1)从具体的问题出发,观察各个数量之间或图形之间的特点以及相互的变化特点;(2)通过类比、计算等方法,从不同的角度、层次发现其相似或相同点;(3)由此及彼、合理联想、大胆猜想、总结规律;(4)通过计算验证规律.