2025届广东省广州市白云区华师附中新世界学校九年级数学第一学期开学经典模拟试题【含答案】

这是一份2025届广东省广州市白云区华师附中新世界学校九年级数学第一学期开学经典模拟试题【含答案】，共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）下列图形中，既是轴对称图形，又是中心对称图形的是（ ）
A．B．C．D．
2、（4分）关于的不等式组恰好有四个整数解，那么的取值范围是（ ）
A．B．C．D．
3、（4分）方程中二次项系数一次项系数和常数项分别是（ ）
A．1，-3，1B．-1，-3，1C．-3，3，-1D．1，3，-1
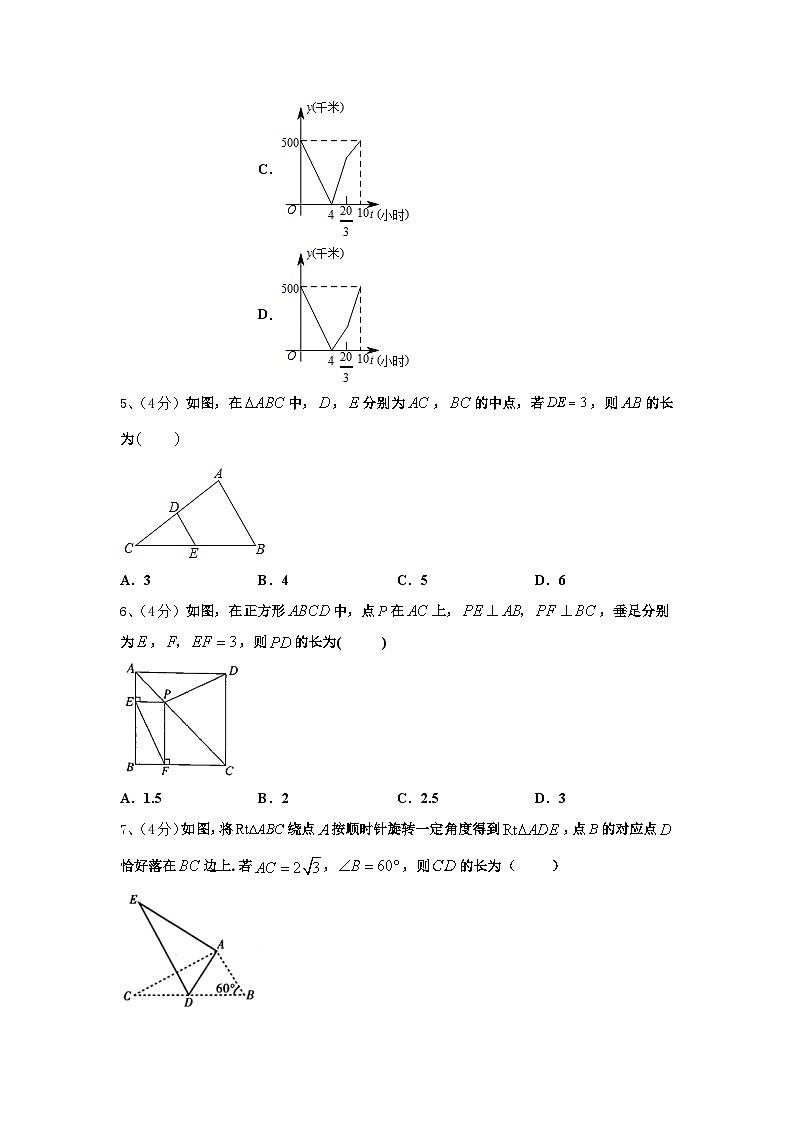
4、（4分）一辆慢车以50千米/小时的速度从甲地驶往乙地，一辆快车以75千米/小时的速度从乙地驶往甲地，甲、乙两地之间的距离为500千米，两车同时出发，则图中折线大致表示两车之间的距离y（千米）与慢车行驶时间t（小时）之间的函数图象是（ ）
A．B．C．D．
5、（4分）如图，在中，，分别为，的中点，若，则的长为
A．3B．4C．5D．6
6、（4分）如图，在正方形中，点在上，，垂足分别为，，则的长为( )
A．1.5B．2C．2.5D．3
7、（4分）如图，将绕点按顺时针旋转一定角度得到，点的对应点恰好落在边上.若，，则的长为（ ）
A．1B．C．2D．
8、（4分）点A，B，C，D在数轴上的位置如图所示，则实数对应的点可能是
A．点AB．点BC．点CD．点D
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）将直线向上平移个单位，得到直线_______。
10、（4分）计算：（π﹣3）0﹣（﹣）﹣2＝_____．
11、（4分）如图，E为正方形ABCD对角线BD上一点，且BE=BC，则∠DCE=_____．
12、（4分）已知一次函数（为常数，且）.若当时，函数有最大值7，则的值为_____.
13、（4分）如图，在直角坐标系中，矩形OABC的顶点B的坐标为（15，6），直线恰好将矩形OABC分成面积相等的两部分，那么b=_____________．
三、解答题（本大题共5个小题，共48分）
14、（12分）阅读下列材料解决问题
两个多位数整数，若它们各数位上的数字之和相等，则称这两个多位数互为“调和数”，例如37和82，它们各数位上的数字之和分别为3+7和8+2，显然3+7＝8+2＝10故37和82互为“调和数”．
（1）下列说法错误的是
A．123和51互为调和数” B．345和513互为“调和数
C．2018和8120互为“调和数” D．两位数和互为“调和数”
（2）若A、B是两个不等的两位数，A＝，B＝，A和B互为“调和数”，且A与B之和是B与A之差的3倍，求满足条件的两位数A．
15、（8分）如图，在△ABC中，CE，BF是两条高，若∠A＝70°，∠BCE＝30°，求∠EBF与∠FBC的度数．
16、（8分）小红同学经常要测量学校旗杆的高度，她发现旗杆的绳子刚好垂到地面上，当她把绳子下端拉开5m后，发现这时绳子的下端正好距地面1m，学校旗杆的高度是（ ）
A．21mB．13mC．10mD．8m
17、（10分）已知：如图，四边形ABCD中，AD∥BC，AD=CD，E是对角线BD上一点，且EA=EC．
（1）求证：四边形ABCD是菱形；
（2）如果BE=BC，且∠CBE：∠BCE=2：3，求证：四边形ABCD是正方形．
18、（10分）如图，在平行四边形中，的平分线交于点，的平分线交于点.
（1）若，，求的长.
（2）求证：四边形是平行四边形.
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）如图，在Rt△ABC中，∠ACB=90°，BC=3，AC=4，AB的垂直平分线DE交BC的延长线于点E，则CE的长为___
20、（4分）已知关于x的方程（m-1）x2-2x+1=0有两个不相等的实数根，则m的取值范围是_____．
21、（4分）如果点A(1，m)与点B(3，n)都在反比例函数y=（k＞0）的图象上，那么代数式m-3n+6的值为______．
22、（4分）若二次根式有意义，则x的取值范围是 ▲ ．
23、（4分） 如图，以Rt△ABC的三边为边向外作正方形，其面积分别为S1、S2、S3，且S1＝5，S2＝6，则AB的长为_____．
二、解答题（本大题共3个小题，共30分）
24、（8分）某校招聘一名数学老师，对应聘者分别进行了教学能力、科研能力和组织能力三项测试，其中甲、乙两名应聘者的成绩如右表：（单位：分）
（1）若根据三项测试的平均成绩在甲、乙两人中录用一人，那么谁将被录用？
（2）根据实际需要，学校将教学、科研和组织能力三项测试得分按 5：3：2 的比确定每人的最后成绩，若按此成绩在甲、乙两人中录用一人，谁将被录用？
25、（10分）化简求值：，其中x=1．
26、（12分）如图所示，在△ABC中，点D为BC边上的一点，AD＝12，BD＝16，AB＝20，CD＝1．
（1）试说明AD⊥BC．
（2）求AC的长及△ABC的面积．
（3）判断△ABC是否是直角三角形，并说明理由．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、C
【解析】
根据轴对称图形和中心对称图形的概念逐一判断即可．
【详解】
A：是轴对称图形，不是中心对称图形．故错误；
B：不是轴对称图形，是中心对称图形．故错误；
C：是轴对称图形，也是中心对称图形．故正确；
D：是轴对称图形，不是中心对称图形．故错误；
故答案选C．
本题主要考查了轴对称图形和中心对称图形的分辨，熟记轴对称和中心对称的有关概念是解题的关键．
2、C
【解析】
可先用m表示出不等式组的解集，再根据恰有四个整数解可得到关于m的不等式，可求得m的取值范围．
【详解】
解：
在中，
解不等式①可得x＞m，
解不等式②可得x≤3，
由题意可知原不等式组有解，
∴原不等式组的解集为m＜x≤3，
∵该不等式组恰好有四个整数解，
∴整数解为0，1，2，3，
∴-1≤m＜0，
故选C．
本题主要考查解不等式组，求得不等式组的解集是解题的关键，注意恰有四个整数解的应用．
3、A
【解析】
先把方程化为一般形式，然后可得二次项系数，一次项系数及常数项.
【详解】
解：把方程转化为一般形式得：x2−3x＋1＝0，
∴二次项系数，一次项系数和常数项分别是1，−3，1．
故选：A．
一元二次方程的一般形式是：ax2＋bx＋c＝0（a，b，c是常数且a≠0）．在一般形式中ax2叫二次项，bx叫一次项，c是常数项．其中a，b，c分别叫二次项系数，一次项系数，常数项．
4、C
【解析】
因为慢车和快车从相距500千米的甲乙两地同时出发,则时间为0小时,两车相距距离为500千米,经过4小时,两车相遇,则此时两车相距距离为0,相遇之后快车经过小时先到达甲地,此时两车相距(75+50) ×=千米>250千米,然后再经过小时,慢车到达乙地,此时两车相距500千米,故选C.
5、D
【解析】
根据三角形的中位线定理得出AB=2DE，把DE的值代入即可．
【详解】
，分别为，的中点，
，
故选：．
本题考查了三角形的中位线平行于第三边并且等于第三边的一半，熟记定理是解题的关键．
6、D
【解析】
作辅助线PB，求证，然后证明四边形是矩形，
【详解】
如图，连接.
在正方形中，.
∵，
∴，∴.
∵，
∴四边形是矩形，
∴.∴.
故选D.
本题考查了全等三角形的判定定理（SAS）以及矩形对角线相等的性质，从而求出PD的长度
7、C
【解析】
先根据旋转的性质判断出是等边三角形，然后设，得到，，利用勾股定理进行计算即可．
【详解】
根据题意可知AB=AD,且∠ABD=60°，
∴是等边三角形，且，
设，
则，，所以，，
在中，，得，（负值已舍）.
故选C.
此题考查旋转的性质，解题关键在于掌握旋转的性质，再利用勾股定理进行计算.
8、B
【解析】
根据被开方数越大算术平方根越大，可得的大小，根据数的大小，可得答案．
【详解】
，
，
实数对应的点可能是B点，
故选B．
本题考查了实数与数轴，利用被开方数越大算术平方根越大得出是解题关键．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、
【解析】
根据平移k不变，b值加减即可得出答案．
【详解】
平移后解析式为：y=2x−1+4=2x+3，
故答案为：y=2x+3
此题考查一次函数图象与几何变换，解题关键在于掌握平移的性质
10、-1．
【解析】
根据零指数幂以及负整数指数幂的意义即可求出答案．
【详解】
解：原式＝1﹣（﹣2）2＝1﹣4＝﹣1
故答案为：﹣1．
本题考查了零指数幂以及负整数指数幂的运算，掌握基本的运算法则是解题的关键．
11、22.5°
【解析】
根据正方形的对角线平分一组对角求出∠CBE=45°，再根据等腰三角形两底角相等求出∠BCE=67.5°，然后根据∠DCE=∠BCD-∠BCE计算即可得解．
【详解】
∵四边形ABCD是正方形，
∴∠CBE=45°，∠BCD=90°，
∵BE=BC，
∴∠BCE=（180°-∠BCE）=×（180°-45°）=67.5°，
∴∠DCE=∠BCD-∠BCE=90°-67.5°=22.5°．
故答案为22.5°．
本题考查了正方形的性质，等腰三角形的性质，主要利用了正方形的对角线平分一组对角，需熟记．
12、a＝2或a=-3.
【解析】
分类讨论：a＞0时，y随x的增大而增大，所以当x=4时，y有最大值7，然后把y=7代入函数关系式可计算出对应a的值；a＜0时，y随x的增大而减小，所以当x=-1时，y有最大值7，然后把x=-1代入函数关系式可计算对应a的值．
【详解】
解：①a＞0时，y随x的增大而增大，
则当x=4时，y有最大值7，把x=4，y=7代入函数关系式得7=4a-a+1，解得a=2；
②a＜0时，y随x的增大而减小，
则当x=-1时，y有最大值7，把x=-1代入函数关系式得 7=-a-a+1，解得a=-3，
所以a＝2或a=-3.
本题考查了一次函数的性质：k＞0，y随x的增大而增大，函数从左到右上升；k＜0，y随x的增大而减小，函数从左到右下降．
13、0.5
【解析】
经过矩形对角线的交点的直线平分矩形的面积．故先求出对角线的交点坐标，再代入直线解析式求解．
【详解】
连接AC、OB，交于D点，作DE⊥OA于E点，
∵四边形OABC为矩形，
∴DE=AB=3，OE=OA=7.5，
∴D(7.5，3)，
∵直线恰好将矩形OABC分成面积相等的两部分，
∴直线经过点D，
∴将(7.5，3)代入直线得：
3=×7.5+b，
解得：b=0.5，
故答案为：0.5.
本题考查了一次函数的综合应用及矩形的性质；找着思考问题的突破口，理解过矩形对角线交点的直线将矩形面积分为相等的两部分是正确解答本题的关键．
三、解答题（本大题共5个小题，共48分）
14、（1）B（2）18
【解析】
（1）根据题意，两个多位数整数，若它们各数位上的数字之和相等，则称这两个多位数互为“调和数”，即可作答
（2）先用“调和数”，得出x+y=m+n，再利用A与B之和是B与A之差的3倍，得出10m+n=20x+2y，即可得出m＝ ，最后利用1≤x≤9，0≤y≤9，计论即可以得出结论
【详解】
（1）根据调和数的定义，通过计算各位数之和，易知B选项错误
故答案选B
（2）∵A＝，B＝，A、B互为“调和数”
∴x+y＝m+n①
∵A与B之和是B与A之差的3倍
∴
∴
∴10m+n＝20x+2y②
由①②得，m=
∵m为两位数的十位数字
∴1≤m≤9
∴1≤≤9,
∴9≤19x+y≤81，且19x+y是9的倍数
∴19x+y＝18或27或36或45或54或63或72或81
则或或或或或或或
∵x，y分别为A的 十位和个位，
∴1≤x≤9，0≤y≤9
∴计算可得，仅当时满足，此时x＝1，y＝8，故A为18
故满足A的值为18
本题考查了整除的问题，新定义解不等式，分类讨论的数学思想，判断出19x+y=18或27或36或45或54或63或72或81是解决（2）的关键
15、∠EBF=20°，∠FBC=40°．
【解析】
试题分析：在Rt△ABF中，∠A=70，CE，BF是两条高，求得∠EBF的度数，在Rt△BCF中∠FBC=40°求得∠FBC的度数．
解：在Rt△ABF中，∠A=70，CE，BF是两条高，
∴∠EBF=20°，∠ECA=20°，
又∵∠BCE=30°，
∴∠ACB=50°，
∴在Rt△BCF中∠FBC=40°．
16、B
【解析】
根据题意设旗杆的高AB为x米，则绳子AC的长为x米，在Rt△ACH利用勾股定理构建方程即可解决问题．
【详解】
如图，已知AB=AC，CD⊥BD，CH⊥AB，CD=BH=1米，CH=5米，设AB=AC=x米．
在Rt△ACH中，∵AC2=AH2+CH2，
∴x2=52+（x-1）2，
∴x=13，
∴AB=13（米），
故选B．
此题考查了勾股定理在实际问题中的应用，能够正确理解题意继而构造直角三角形是解决本题的关键，难度一般．
17、（1）证明见解析；（2）证明见解析.
【解析】
（1）首先证得△ADE≌△CDE，由全等三角形的性质可得∠ADE=∠CDE，由AD∥BC可得∠ADE=∠CBD，易得∠CDB=∠CBD，可得BC=CD，易得AD=BC，利用平行线的判定定理可得四边形ABCD为平行四边形，由AD=CD可得四边形ABCD是菱形；
（2）由BE=BC可得△BEC为等腰三角形，可得∠BCE=∠BEC，利用三角形的内角和定理可得∠CBE=180× =45°，易得∠ABE=45°，可得∠ABC=90°，由正方形的判定定理可得四边形ABCD是正方形．
【详解】
（1）在△ADE与△CDE中，
，
∴△ADE≌△CDE，
∴∠ADE=∠CDE，
∵AD∥BC，
∴∠ADE=∠CBD，
∴∠CDE=∠CBD，
∴BC=CD，
∵AD=CD，
∴BC=AD，
∴四边形ABCD为平行四边形，
∵AD=CD，
∴四边形ABCD是菱形；
（2）∵BE=BC，
∴∠BCE=∠BEC，
∵∠CBE：∠BCE=2：3，
∴∠CBE=180× =45°，
∵四边形ABCD是菱形，
∴∠ABE=45°，
∴∠ABC=90°，
∴四边形ABCD是正方形．
18、（1）；（2）证明见解析.
【解析】
（1）根据等腰三角形的性质即可求解；
（2）根据角平分线的性质及平行线的判定得到，再根据即可证明.
【详解】
（1）解：∵四边形为平形四边形
∴
∵平分
∴
∴
∴，
∴
（2）证明：∵四边形为平行四边形
∴
∵平分
又∴
∴
∴
∴四边形为平行四边形
此题主要考查平行四边形的性质与判定，解题的关键是熟知平行四边形的性质定理.
一、填空题（本大题共5个小题，每小题4分，共20分）
19、
【解析】
设CE=x，连接AE，由线段垂直平分线的性质可知AE=BE=BC+CE，在Rt△ACE中，利用勾股定理即可求出CE的长度，
【详解】
∵ DE是线段AB的垂直平分线，
∴AE=BE=BC+CE=3+x，
∴在Rt△ACE中，AE2=AC2+CE2，即（3+x）2=42+x2，
解得x=．
20、m＜2且m≠1．
【解析】
根据一元二次根的判别式及一元二次方程的定义求解．
【详解】
解：∵关于x的方程（m-1）x2-2x+1=0有两个不相等的实数根，
∴m-1≠0，且△＞0，即4-4（m-1）＞0，解得m＜2，
∴m的取值范围是：m＜2且m≠1．
故答案为：m＜2且m≠1．
本题考查根的判别式及一元二次方程的定义，掌握公式正确计算是解题关键．
21、1
【解析】
点A（1，m）与点B（3，n）都在反比例函数y=（k＞0）的图象上，代入可求出m、n，进而求代数式的值．
【详解】
解；把点A（1，m）、B（3，n）代入y=得：m=3，n=1
∴m-3n+1=3-3×1+1=1．
故答案为：1．
考查反比例函数图象上点的坐标特点，理解函数图象的意义，正确的代入和细心的计算是解决问题的前提．
22、．
【解析】
根据二次根式有意义的条件：被开方数大于等于0列出不等式求解.
【详解】
根据二次根式被开方数必须是非负数的条件，得.
本题考查二次根式有意义的条件，牢记被开方数必须是非负数.
23、
【解析】
根据勾股定理得出S2+S1＝S3，求出S3，即可求出AB．
【详解】
解：∵由勾股定理得：AC2+BC2＝AB2，
∴S2+S1＝S3，
∵S1＝5，S2＝6，
∴S3＝11，
∴AB＝，
故答案为：．
本题考查了勾股定理和正方形的性质，能求出S3的值是解此题的关键．
二、解答题（本大题共3个小题，共30分）
24、（1）甲被录用；（2）乙被录用．
【解析】
分析:（1）根据平均数的计算公式分别进行计算，平均数大的将被录用；
（2）根据加权平均数的计算公式分别进行解答，加权平均数大的将被录用；
详解: （1）甲的平均成绩为=84（分）；
乙的平均成绩为=82（分），
因为甲的平均成绩高于乙的平均成绩，
所以甲被录用；
（2）根据题意，甲的平均成绩为=83.2（分），
乙的平均成绩为=84.8（分），
因为甲的平均成绩低于乙的平均成绩，
所以乙被录用．
点睛: 本题重点考查了算术平均数和加权平均数的计算公式，希望同学们要牢记这些公式，并能够灵活运用.
数据x1、x2、……、xn的算术平均数：=(x1+x2+……+xn)，
加权平均数：（其中w1、w2、……wn为权数）.
算术平均数是加权平均数的一种特殊情况，加权平均数包含算术平均数，当加权平均数中的权相等时，就是算术平均数.
25、3x+2，2.
【解析】
先将括号内异分母分式通分计算，再将除法变乘法，约分化简，再代入数据计算.
【详解】
解：原式=
=
=3x+2，
当x=1时，原式=2．
本题考查分式的化简求值，熟练掌握分式的通分与约分是解题的关键.
26、（1）见解析；（2）15，150；（3）是
【解析】
试题分析：（1）根据勾股定理的逆定理即可判断；
（2）先根据勾股定理求得斜边的长，再根据直角三角形的面积公式即可求得结果；
（3）根据勾股定理的逆定理即可判断.
（1）
∴是直角三角形
∴即；
（2）∵，且点为边上的一点
∴
∴由勾股定理得：
∴；
（3）是直角三角形
，
∴是直角三角形.
考点：本题考查的是勾股定理，直角三角形的面积公式，勾股定理的逆定理
点评：解答本题的根据是熟练掌握勾股定理的逆定理：如果三角形有两边的平方和等于第三边的平方，那么这个是直角三角形.
题号
一
二
三
四
五
总分
得分
教学能力
科研能力
组织能力
甲
81
85
86
乙
92
80
74