

2024年吉林省通化市外国语学校九年级数学第一学期开学达标测试试题【含答案】
展开一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)
1、(4分)点,,若将线段平移到线段,使点到达点,则点的坐标是( )
A.B.C.D.
2、(4分)如图,在平面直角坐标系中,线段AB的端点坐标为A(-2,4),B(4,2),直线y=kx-2与线段AB有交点,则K的值不可能是( )
A.-5B.-2C.3D.5
3、(4分)若分式方程有增根,则a的值是( )
A.4B.3C.2D.1
4、(4分)一次函数的图像不经过第四象限,那么的取值范围是( )
A.B.C.D.
5、(4分)如图,在平行四边形ABCD中,对角线AC、BD交于点O,E是CD的中点,若OE=2,则AD的长为( )
A.2B.3
C.4D.5
6、(4分)如图,点C是线段AB的黄金分割点(AC>BC),下列结论错误的是( )
A.B.C.D.
7、(4分)若是关于的一元二次方程,则的取值范围是( )
A.B.C.D.
8、(4分)若点都是反比例函数的图象上的点,并且,则下列各式中正确的是(( )
A.B.C.D.
二、填空题(本大题共5个小题,每小题4分,共20分)
9、(4分)根式+1的相反数是_____.
10、(4分)若一个正多边形的一个内角等于135°,那么这个多边形是正_____边形.
11、(4分)如图所示,将直角三角形, ,,沿方向平移得直角三角形,,阴影部分面积为_____________.
12、(4分)在●〇●〇〇●〇〇〇●〇〇〇〇●〇〇〇〇〇中,空心圈“〇”出现的频率是_____.
13、(4分)一组正整数2,4,5,从小到大排列,已知这组数据的中位数和平均数相等,那么的值是______.
三、解答题(本大题共5个小题,共48分)
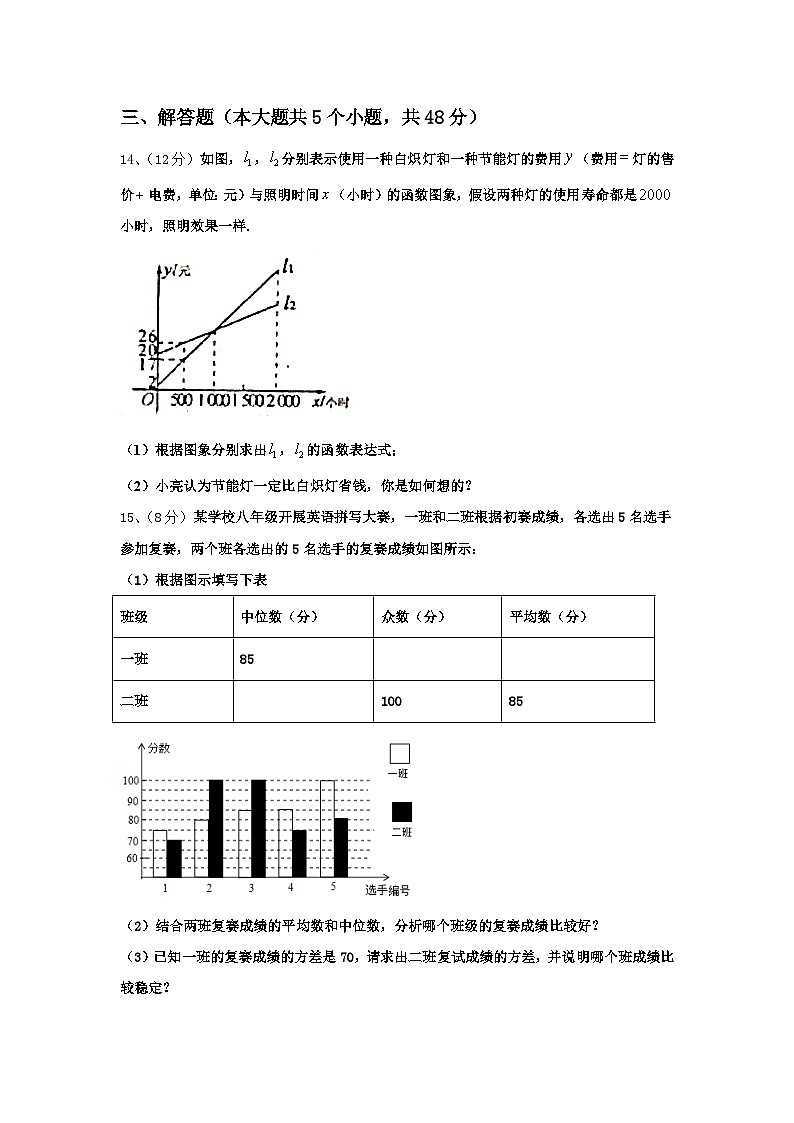
14、(12分)如图,,分别表示使用一种白炽灯和一种节能灯的费用(费用灯的售价电费,单位:元)与照明时间(小时)的函数图象,假设两种灯的使用寿命都是小时,照明效果一样.
(1)根据图象分别求出,的函数表达式;
(2)小亮认为节能灯一定比白炽灯省钱,你是如何想的?
15、(8分)某学校八年级开展英语拼写大赛,一班和二班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示:
(1)根据图示填写下表
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩比较好?
(3)已知一班的复赛成绩的方差是70,请求出二班复试成绩的方差,并说明哪个班成绩比较稳定?
16、(8分)解不等式:
17、(10分)某个体户购进一批时令水果,20天销售完毕,他将本次的销售情况进行了跟踪记录,根据所记录的数据绘制如图所示的函数图象,其中日销售量y(千克)与销售时间x(天)之间的函数关系如图甲,销售单价P(元/千克)与销售时间x(天)之间的关系如图乙.
(1)求y与x之间的函数关系式.
(2)分别求第10天和第15天的销售金额.
(3)若日销售量不低于24千克的时间段为“最佳销售期”,则此次销售过程中“最佳销售期”共有多少天?在此期间销售单价最高为多少元?
18、(10分)观察下列一组方程:;;;;它们的根有一定的规律,都是两个连续的自然数,我们称这类一元二次方程为“连根一元二次方程”.
若也是“连根一元二次方程”,写出k的值,并解这个一元二次方程;
请写出第n个方程和它的根.
B卷(50分)
一、填空题(本大题共5个小题,每小题4分,共20分)
19、(4分)某果园2011年水果产量为100吨,2013年水果产量为144吨,求该果园水果产量的年平均增长率.设该果园水果产量的年平均增长率为x,则根据题意可列方程为_____.
20、(4分)如图,在△ABC中,∠B=∠C=60°,点D在AB边上,DE⊥AB,并与AC边交于点E.如果AD=1,BC=6,那么CE等于______.
21、(4分)如图,矩形中,, 将矩形绕点顺时针旋转,点分别落在点处,且点在同一条直线上,则的长为__________.
22、(4分)当x=2时,二次根式的值为________.
23、(4分)某高科技开发公司从2013年起开始投入技术改进资金,经过技术改进后,其产品的生产成本不断降低,具体数据如下表:请你认真分析表中数据,写出可以表示该变化规律的表达式是____________.
二、解答题(本大题共3个小题,共30分)
24、(8分)我市经济技术开发区某智能手机有限公司接到生产300万部智能手机的订单,为了尽快交货,增开了一条生产线,实际每月生产能力比原计划提高了50%,结果比原计划提前5个月完成交货,求每月实际生产智能手机多少万部.
25、(10分)一个批发兼零售的文具店规定:凡一次购买铅笔300枝以上,(不包括300枝),可以按批发价付款,购买300枝以下,(包括300枝)只能按零售价付款.小明来该店购买铅笔,如果给八年级学生每人购买1枝,那么只能按零售价付款,需用120元,如果购买60枝,那么可以按批发价付款,同样需要120元,
(1) 这个八年级的学生总数在什么范围内?
(2) 若按批发价购买6枝与按零售价购买5枝的款相同,那么这个学校八年级学生有多少人?
26、(12分)如图所示,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=3,BC=4,求四边形OCED的周长.
参考答案与详细解析
一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)
1、C
【解析】
因为A和C是平移的对应点,根据平移的性质和点B的坐标可得结果.
【详解】
解:∵经过平移,A到达C,A(-4,-3),C(1,-1),
∴线段AB平移到线段CD是向左平移5个单位,再向上平移2个单位,
∵ B(-1,2),
∴点D的坐标是(4,4).
故选C.
本题考查了图形的平移,掌握平移的性质是解题的关键.
2、B
【解析】
当直线y=kx-2与线段AB的交点为A点时,把A(-2,4)代入y=kx-2,求出k=-3,根据一次函数的有关性质得到当k≤-3时直线y=kx-2与线段AB有交点;当直线y=kx-2与线段AB的交点为B点时,把B(4,2)代入y=kx-2,求出k=1,根据一次函数的有关性质得到当k≥1时直线y=kx-2与线段AB有交点,从而能得到正确选项.
【详解】
把A(-2,4)代入y=kx-2得,4=-2k-2,解得k=-3,
∴当直线y=kx-2与线段AB有交点,且过第二、四象限时,k满足的条件为k≤-3;
把B(4,2)代入y=kx-2得,4k-2=2,解得k=1,
∴当直线y=kx-2与线段AB有交点,且过第一、三象限时,k满足的条件为k≥1.
即k≤-3或k≥1.
所以直线y=kx-2与线段AB有交点,则k的值不可能是-2.
故选B.
本题考查了一次函数y=kx+b(k≠0)的性质:当k>0时,图象必过第一、三象限,k越大直线越靠近y轴;当k<0时,图象必过第二、四象限,k越小直线越靠近y轴.
3、A
【解析】
要使分式方程有增根,则首先判断增根,再将增根代入化简后的方程中计算参数即可.
【详解】
解:原方程两边同乘以(x﹣3)得
1+(x﹣3)=a﹣x
∵方程有增根,
∴将x=3代入得
1+(3﹣3)=a﹣3
∴a=4
故选:A.
本题主要考查分式方程中增根的计算,关键在于准确的判断增根.
4、A
【解析】
根据一次函数经过的象限即可确定,解不等式即可得出的取值范围.
【详解】
∵一次函数的图像不经过第四象限,
∴,
解得,
故选:A.
本题主要考查一次函数的图象及性质,掌握一次函数的图象及性质是解题的关键.
5、C
【解析】
平行四边形中对角线互相平分,则点O是BD的中点,而E是CD边中点,根据三角形两边中点的连线平行于第三边且等于第三边的一半可得AD=1.
【详解】
解:∵四边形ABCD是平行四边形,
∴OB=OD,OA=OC.
又∵点E是CD边中点,
∴AD=2OE,即AD=1.
故选:C.
此题主要考查了平行四边形的性质及三角形中位线定理,三角形中位线性质应用比较广泛,尤其是在三角形、四边形方面起着非常重要作用.
6、B
【解析】
∵AC>BC,
∴AC是较长的线段,
根据黄金分割的定义可知:= ≈0.618,
故A、C、D正确,不符合题意;
AC2=AB•BC,故B错误,符合题意;
故选B.
7、B
【解析】
根据一元二次方程的定义即可求出答案.
【详解】
解:由题意可知:a﹣1≠0,
∴a≠1,
故选:B.
本题考查一元二次方程的定义,解题的关键是正确理解一元二次方程的定义,本题属于基础题型.
8、B
【解析】
解:根据题意可得:
∴反比例函数处于二、四象限,则在每个象限内为增函数,
且当x<0时y>0,当x>0时,y<0,
∴<<.
二、填空题(本大题共5个小题,每小题4分,共20分)
9、
【解析】
本题考查了实数的性质,在一个数的前面加上负号就是这个数的相反数.
【详解】
解: +1的相反数是﹣﹣1,
故答案为:﹣﹣1.
本题考查了实数的性质,在一个数的前面加上负号就是这个数的相反数.
10、八
【解析】
360°÷(180°-135°)=8
11、1
【解析】
根据平移的性质,对应点间的距离等于平移的距离求出CE=BF,再求出GE,然后根据平移变换只改变图形的位置不改变图形的形状与大小可得△ABC的面积等于△DEF的面积,从而得到阴影部分的面积等于梯形ACEG的面积,再利用梯形的面积公式列式计算即可得解.
【详解】
∵△ACB平移得到△DEF,
∴CE=BF=2,DE=AC=6,
∴GE=DE-DG=6-3=3,
由平移的性质,S△ABC=S△DEF,
∴阴影部分的面积=S梯形ACEG=(GE+AC)•CE=(3+6)×2=1.
故答案为:1.
本题考查了平移的性质,熟练掌握性质并求出阴影部分的面积等于梯形ACEG的面积是本题的难点,也是解题的关键.
12、0.1
【解析】
用空心圈出现的频数除以圆圈的总数即可求解.
【详解】
解:由图可得,总共有20个圆,出现空心圆的频数是15,频率是15÷20=0.1.
故答案是:0.1.
考查了频率的计算公式:频率=频数÷数据总数,是需要识记的内容.
13、1
【解析】
根据这组数据的中位数和平均数相等,得出(4+5)÷2=(2+4+5+x)÷4,求出x的值即可.
【详解】
∵这组数据的中位数和平均数相等,
∴(4+5)÷2=(2+4+5+x)÷4,
解得:x=1.
故答案为:1.
此题考查了中位数和平均数,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,关键是根据中位数和平均数相等列出方程.
三、解答题(本大题共5个小题,共48分)
14、(1)的函数表达式为,的函数表达式为;(2)小亮的想法是错误的,若两灯同时点亮,当时,白炽灯省钱;当时,两种灯费用相同;当时,节能灯省钱.
【解析】
(1)根据函数图象中的数据可以分别求得l1、l2的函数关系式;
(2)根据(1)中的函数解析式可以求得两种灯泡费用相同的情况,然后根据图象即可解答本题.
【详解】
解:(1)设的函数表达式为:将,代入得
的函数表达式为
设的函数表达式为:
将,代入得
的函数表达式为
(2)小亮的想法是错误的,若两灯同时点亮,
由,,当时,白炽灯省钱;
由,,当时,两种灯费用相同;
由,,当时,节能灯省钱.
本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
15、(1)85、85 80(2)一班成绩好些.因为两班平均数相等,一班的中位数高,所以一班成绩好些.(回答合理即可)(3)一班成绩较为稳定.
【解析】
(1)观察图分别写出一班和二班5名选手的复赛成绩,然后根据中位数的定义和平均数的求法以及众数的定义求解即可;
(2)在平均数相同的情况下,中位数高的成绩较好;
(3)根据方差公式计算即可:S2=(可简单记忆为“等于差方的平均数”)
【详解】
解:(1)由条形统计图可知一班5名选手的复赛成绩为:75、80、85、85、100,
二班5名选手的复赛成绩为:70、100、100、75、80,
一班的众数为85,
一班的平均数为(75+80+85+85+100)÷5=85,
二班的中位数是80;
故填: 85、85 80
(2)一班成绩好些.因为两班平均数相等,一班的中位数高,所以一班成绩好些.(回答合理即可)
(3)S二班2=
因为S一班2=70则S一班2<S二班2,因此一班成绩较为稳定.
本题考查了中位数、众数以及平均数的求法,同时也考查了方差公式,解题的关键是牢记定义并能熟练运用公式.
16、.
【解析】
根据解一元一次不等式基本步骤:去分母、去括号、移项、合并同类项、系数化为1可得.
【详解】
,
,
,
.
本题主要考查解一元一次不等式的基本能力,严格遵循解不等式的基本步骤是关键,尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变.
17、 (1)当;(2)第10天:200元,第15天:270元;(3)最佳销售期有5天,最高为9.6元.
【解析】
(1)分两种情况进行讨论:①0≤x≤15;②15<x≤20,针对每一种情况,都可以先设出函数的解析式,再将已知点的坐标代入,利用待定系数法求解;
(2)日销售金额=日销售单价×日销售量.由于第10天和第15天在第10天和第20天之间,当10≤x≤20时,设销售单价p(元/千克)与销售时间x(天)之间的函数关系式为p=mx+n,由点(10,10),(20,8)在p=mx+n的图象上,利用待定系数法求得p与x的函数解析式,继而求得10天与第15天的销售金额.
(3)日销售量不低于1千克,即y≥1.先解不等式2x≥1,得x≥12,再解不等式﹣6x+120≥1,得x≤16,则求出“最佳销售期”共有5天;然后根据.(10≤x≤20),利用一次函数的性质,即可求出在此期间销售时单价的最高值.
【详解】
解:(1)①当0≤x≤15时,设日销售量y与销售时间x的函数解析式为y=k1x,
∵直线y=k1x过点(15,30),∴15k1=30,解得k1=2.
∴y=2x(0≤x≤15);
②当15<x≤20时,设日销售量y与销售时间x的函数解析式为y=k2x+b,
∵点(15,30),(20,0)在y=k2x+b的图象上,
∴,解得:.
∴y=﹣6x+120(15<x≤20).
综上所述,可知y与x之间的函数关系式为:.
.
(2)∵第10天和第15天在第10天和第20天之间,
∴当10≤x≤20时,设销售单价p(元/千克)与销售时间x(天)之间的函数解析式为p=mx+n,
∵点(10,10),(20,8)在z=mx+n的图象上,,
解得:.
∴.
当x=10时,,y=2×10=20,销售金额为:10×20=200(元);
当x=15时,,y=2×15=30,销售金额为:9×30=270(元).
故第10天和第15天的销售金额分别为200元,270元.
(3)若日销售量不低于1千克,则y≥1.
当0≤x≤15时,y=2x,
解不等式2x≥1,得x≥12;
当15<x≤20时,y=﹣6x+120,
解不等式﹣6x+120≥1,得x≤16.
∴12≤x≤16.
∴“最佳销售期”共有:16﹣12+1=5(天).
∵(10≤x≤20)中<0,∴p随x的增大而减小.
∴当12≤x≤16时,x取12时,p有最大值,此时=9.6(元/千克).
故此次销售过程中“最佳销售期”共有5天,在此期间销售单价最高为9.6元
考核知识点:一次函数在销售中的运用.要注意理解题意,分类讨论情况.
18、(1)x1=7,x2=8.(2)x1=n-1,x2=n.
【解析】
(1)根据十字相乘的方法和“连根一元二次方程”的定义,找到56是7与8的乘积,确定k值即可解题,(2)找到规律,十字相乘的方法即可求解.
【详解】
解:(1)由题意可得k=-15,则原方程为x2-15x+56=0,则(x-7)·(x-8)=0,解得x1=7,x2=8.
(2)第n个方程为x2-(2n-1)x+n(n-1)=0,(x-n)(x-n+1)=0,解得x1=n-1,x2=n.
本题考查了用因式分解法求解一元二次方程,与十字相乘联系密切,连根一元二次方程是特殊的十字相乘,中等难度,会用十字相乘解题是解题关键.
一、填空题(本大题共5个小题,每小题4分,共20分)
19、100(1+x)2=1
【解析】分析:2013年的产量=2011年的产量×(1+年平均增长率)2,把相关数值代入即可.
详解:设该果园水果产量的年平均增长率为x,根据题意,得:
100(1+x)2=1,
故答案为:100(1+x)2=1.
点睛:本题考查了由实际问题抽象出一元二次方程;得到2013年产量的等量关系是解决本题的关键.
20、4
【解析】
根据等边三角形的性质和含30°的直角三角形的性质解答即可.
【详解】
∵在△ABC中,∠B=∠C=60°,
∴∠A=60°,
∵DE⊥AB,
∴∠AED=30°,
∵AD=1,
∴AE=2,
∵BC=6,
∴AC=BC=6,
∴CE=AC−AE=6−2=4.
故答案为4.
本题考查了等边三角形的性质,解题的关键是熟练的掌握等边三角形的性质.
21、
【解析】
根据平行的性质,列出比例式,即可得解.
【详解】
设的长为
根据题意,得
∴
又∵
∴
∴
解得(不符合题意,舍去)
∴的长为.
此题主要考查矩形的性质,关键是列出关系式,即可解题.
22、3
【解析】
【分析】把x=2代入二次根式进行计算即可得.
【详解】把x=2代入得,
==3,
故答案为:3.
【点睛】本题考查了二次根式的值,准确计算是解题的关键.
23、y=
【解析】
有表格中数据分析可知xy=2.5×7.2=3×6=4×4.5=4.5×4=18,就可得到反比例函数关系,再设出反比例函数解析式,利用待定系数法求出即可.
【详解】
由题意可得此函数解析式为反比例函数解析式,设其为解析式为y=.
当x=2.5时,y=7.2,
可得7.2=,
解得k=18
∴反比例函数是y=.
此题主要考查反比例函数的应用,解题的关键是根据题意找出等量关系.
二、解答题(本大题共3个小题,共30分)
24、每月实际生产智能手机1万部.
【解析】
分析:设原计划每月生产智能手机x万部,则实际每月生产智能手机(1+50%)x万部,根据工作时间=工作总量÷工作效率结合提前5个月完成任务,即可得出关于x的分式方程,解之经检验后即可得出结论.
详解:设原计划每月生产智能手机x万部,则实际每月生产智能手机(1+50%)x万部,
根据题意得:,
解得:x=20,
经检验,x=20是原方程的解,且符合题意,
∴(1+50%)x=1.
答:每月实际生产智能手机1万部.
点睛:本题考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键.
25、(1)240人<八年级学生数≤300人
(2)这个学校八年级学生有300人.
【解析】
答:八年级学生总数为人
(1)关系式为:学生数≤300,学生数+60>300列式求值即可;
(2)批发价为每支x元,则零售价为每支元,列方程求解
【详解】
解:(1)有已知,240人<总数≤300人;
(2)批发价为每支x元,则零售价为每支元
可列方程
求得x=
经检验x=符合题意
学生总数为人
26、(1)菱形(2)1
【解析】
(1)根据DE∥AC,CE∥BD.得出四边形OCED是平行四边形,根据矩形的性质求得OC=OD,即可判定四边形OCED是菱形;(2)利用勾股定理求得AC的长,从而得出该菱形的边长,即可得出答案.
【详解】
(1)四边形OCED是菱形.
∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
在矩形ABCD中,OC=OD,
∴四边形OCED是菱形.
(2)∵四边形ABCD是矩形,
∴AC===5,
∴CO=OD=,
∴四边形OCED的周长=4×=1.
此题考查了菱形的判定与性质以及矩形的性质.根据连线的判定定理证得四边形CODE是菱形是解此题的关键.
题号
一
二
三
四
五
总分
得分
班级
中位数(分)
众数(分)
平均数(分)
一班
85
二班
100
85
班级
中位数(分)
众数(分)
平均数(分)
一班
85
85
85
二班
80
100
85
2024-2025学年深圳市外国语学校数学九年级第一学期开学达标检测试题【含答案】: 这是一份2024-2025学年深圳市外国语学校数学九年级第一学期开学达标检测试题【含答案】,共19页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2024-2025学年广东省广州市广州外国语学校数学九年级第一学期开学达标检测试题【含答案】: 这是一份2024-2025学年广东省广州市广州外国语学校数学九年级第一学期开学达标检测试题【含答案】,共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
吉林省通化市外国语学校2023-2024学年数学九上期末达标检测试题含答案: 这是一份吉林省通化市外国语学校2023-2024学年数学九上期末达标检测试题含答案,共7页。试卷主要包含了方程x2=3x的解为,一元二次方程配方为等内容,欢迎下载使用。












