

还剩6页未读,
继续阅读
辽宁省铁岭市开原市2024-2025学年九年级上学期9月月考数学试题
展开
这是一份辽宁省铁岭市开原市2024-2025学年九年级上学期9月月考数学试题,共9页。试卷主要包含了下列说法正确的是,关于的方程的根的情况是,如图,矩形中,,在轴上等内容,欢迎下载使用。
一.选择题(共10小题,满分30分,每小题3分)
1.下列方程中,属于一元二次方程的是( )
A.B.C.D.
2.下列说法正确的是( )
A.对角线相等的四边形是矩形B.对角线互相垂直的四边形是菱形
C.对角线相等的平行四边形是矩形D.对角线互相平分的四边形是菱形
3.关于的方程的根的情况是( )
A.有两个相等的实数根B.有两个不相等的实数根
C.只有一个实数根D.无实数根
4.关于的方程是一元二次方程,则的值是( )
A.B.1C.D.0
5.如图,已知在平面直角坐标系中,四边形是菱形,其中点的坐标是,点的坐标是,点在轴上,则点的坐标是( )
A.B.C.D.
6.如图,矩形中,,在轴上.且点的横坐标为,若以点为圆心,对角线的长为半径作弧交轴的正半轴于,则点的坐标为( )
A.B.C.D.
7.如图,菱形的对角线交于点,点为的中点,连接.若,、则的长为( )
A.4B.3C.D.
8.摩拜共享单车计划2023年第三季度(8,9,10月)连续3个月对成都投放新型摩拜单车,计划8月投放3000台,第三季度共投放12000台,每月按相同的增长率投放,设增长率为,则可列方程( )
A.B.
C.D.
9.在长为30m,宽为20m的长方形田地中开辟三条入口宽度相等的道路,已知剩余田地的面积为,求道路的宽度设道路的宽度为,则可列方程( )
A.B.
C.D.
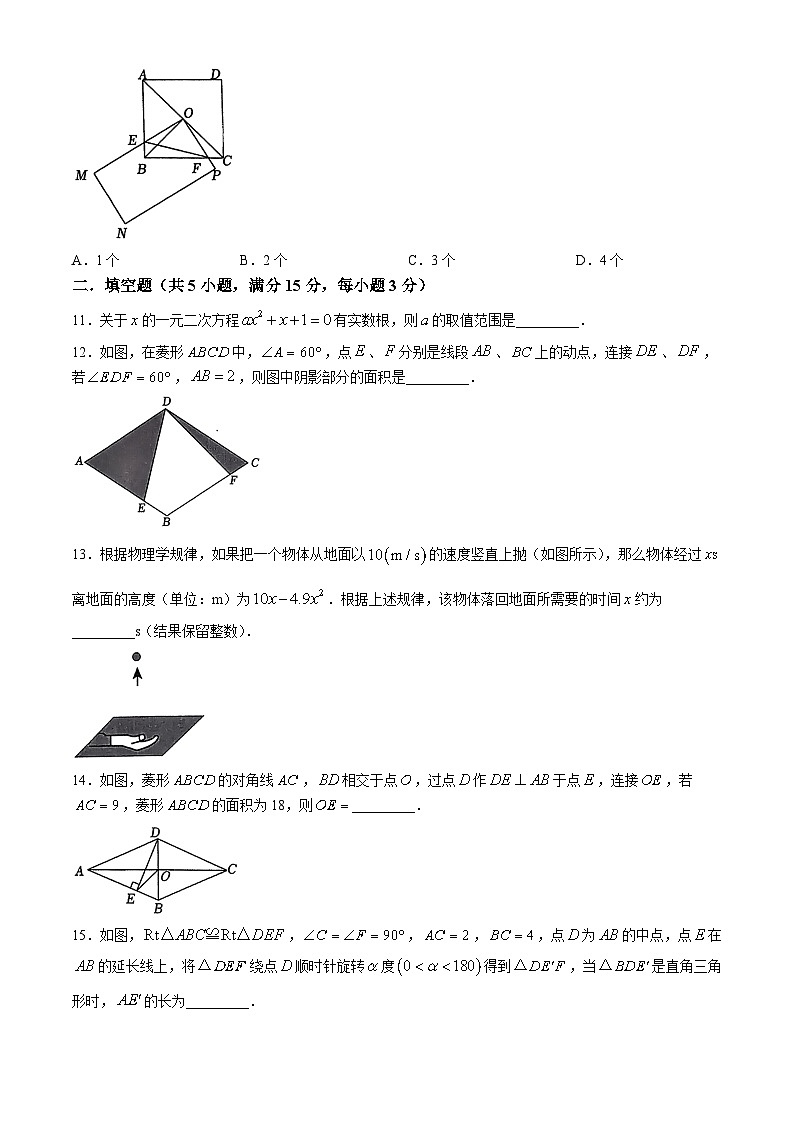
10.如图,正方形中,点为对角线的中点,矩形两边分别交、边于、两点,连接,下列结论正确的有( )个.
(1);
(2);
(3);
(4)若,则以为斜边的直角三角形面积的最大值为8.
A.1个B.2个C.3个D.4个
二.填空题(共5小题,满分15分,每小题3分)
11.关于的一元二次方程有实数根,则的取值范围是_________.
12.如图,在菱形中,,点、分别是线段、上的动点,连接、,若,,则图中阴影部分的面积是_________.
13.根据物理学规律,如果把一个物体从地面以的速度竖直上抛(如图所示),那么物体经过离地面的高度(单位:m)为.根据上述规律,该物体落回地面所需要的时间约为_________s(结果保留整数).
14.如图,菱形的对角线,相交于点,过点作于点,连接,若,菱形的面积为18,则_________.
15.如图,,,,,点为的中点,点在的延长线上,将绕点顺时针旋转度得到,当是直角三角形时,的长为_________.
三.解答题(共8小题,满分75分)
16.(8分)解方程:
(1);(2)
17.(8分)已知关于的一元二次方程.
(1)求证:该方程总有两个不相等的实数根;
(2)若是该方程的一个解,求方程的另一个根.
18.(10分)如图,在平面直角坐标系中,三个顶点的坐标分别为,,.
(1)画出将向左平移4个单位后得到的图形;
(2)画出将绕点按逆时针方向旋转后得到的图形,并直接写出四边形的形状;
(3)在平面内有一点,当以,,,为顶点的四边形是平行四边形时,请直接写出点的坐标.
19.(8分)如图,在平行四边形中,是上一点(不与点,重合),,过点作,交于点,连接,.
(1)求证:四边形是矩形;
(2)当,时,求的长.
20.(9分)如图,在中,,过点的直线,为边上点,过点作交直线与,垂足为,连接,.
(1)求证:;
(2)当在中点时,四边形是什么特殊四边形?说明理由;
21.(10分)三星堆遗址被称为20世纪人类最伟大的考古发现之一,昭示了长江流域与黄河流域一样,同属中华文明的母体,被誉为“长江文明之源”.为更好的传承和宣传三星堆文化,三星堆文创馆一次次打破了自身限定,让文创产品充满创意.已知文创产品“青铜鸟文创水杯”有,两个系列,系列产品比系列产品的售价低5元,100元购买系列产品的数量与150元购买系列产品的数量相等.按定价销售一段时间后发现:系列产品按定价销售,每天可以卖50件,若系列产品每降1元,则每天可以多卖10件.
(1)系列产品和系列产品的单价各是多少?
(2)为了使系列产品每天的销售额为960元,而且尽可能让顾客得到实惠,求系列产品的实际售价应定为多少元/件?
22.(10分)综合实践——用矩形硬纸片制作无盖纸盒.如图1,有一张长30cm,宽16cm的长方形硬纸片,裁去角上同样大小的四个小正方形之后,折成图2所示的无盖纸盒.(硬纸片厚度忽略不计)
(1)若剪去的正方形的边长为2cm,则纸盒底面长方形的长为_________cm,宽为_________cm;
(2)若纸盒的底面积为,请计算剪去的正方形的边长;
(3)如图3,小明先在原矩形硬纸片的两个角各剪去一个同样大小的正方形(阴影部分),经过思考他发现,再剪去两个同样大小的矩形后,可将剩余部分折成一个有盖纸盒.若折成的有盖长方体纸盒的表面积为,请计算剪去的正方形的边长.
23.(12分)在菱形中,,点在对角线上运动(点不与点,点重合),,以点为顶点作菱形;且菱形与菱形的形状、大小完全相同,即,,在菱形绕点旋转的过程中,与边交于点,与边交于点.
【特例感知】
(1)如图1,当,时,则,,之间满足的数量关系是_________;
【类比探究】
(2)如图2,菱形的边长为8,,求的值(用含的代数式表示);
【拓展应用】
(3)在(2)的条件下,连接,,,求的长度.
九上数学北师大(一)
参考答案与试题解析
一.选择题
1-5.DCABC. 6-10. CCDAB.
二.填空题
11. a≤14且a≠0. 12. 13. 2. 14.2. 15. 5或35.
三.解答题(共8小题,满分75分)
16.(8分)(每题4分)
解:(1)x2﹣6x+8=0,
因式分解得,(x﹣2)(x﹣4)=0,x﹣2=0,x﹣4=0,
解得,x1=4,x2=2;
(2)x2﹣3x+1=0
∵a=1,b=﹣3,c=1,∴b2﹣4ac=(﹣3)2﹣4×1×1=5>0,
∴,
∴,.
17.(8分)(1)证明:∵在一元二次方程x2+(n+2)x+n=0中,a=1,b=n+2,c=n,
∴Δ=b2﹣4ac=(n+2)2﹣4n=n2+4>0,
∴方程总有两个不相等的实数根.
(2)解:∵x=﹣2是该方程的一个解,
∴(﹣2)2﹣2(n+2)+n=0,解得n=0,
∴该方程为x2+2x=0,解得x1=﹣2,x2=0,∴方程的另一个根为x=0.
18.(10分)
【解答】解:(1)如图,△A1B1C1即为所求.3分
(2)如图,△A2B2C即为所求. 5分
由旋转得,BC=B2C,AC=A2C,∴四边形A2B2AB为平行四边形.
(3)如图,点D1,D2,D3均满足题意,
∴满足题意的点D的坐标为(2,4)或(4,0)或(﹣2,﹣2).
19.(8分)(1)证明:∵∠BPQ=∠BPC+∠CPQ=∠A+∠AQP,∠BPC=∠AQP,
∴∠CPQ=∠A,
∵PQ⊥CP,∴∠A=∠CPQ=90°,∴平行四边形ABCD是矩形;
(2)解:∵四边形ABCD是矩形,
∴∠D=∠CPQ=90°,
在Rt△CDQ和Rt△CPQ中,,
∴Rt△CDQ≌Rt△CPQ(HL),∴DQ=PQ,
设AQ=x,则DQ=PQ=9﹣x,
在Rt△APQ中,AQ2+AP2=PQ2,∴x2+32=(9﹣x)2,解得:x=4,
∴AQ的长是4.
20.(9分)(1)证明:∵DE⊥BC,∴∠DFB=90°,
∵∠ACB=90°,∴∠ACB=∠DFB,∴AC∥DE,
∵MN∥AB,即CE∥AD,∴四边形ADEC是平行四边形,∴CE=AD;
(2)解:四边形BECD是菱形,理由如下:
∵D为AB中点,∴AD=BD,∵CE=AD,∴BD=CE,
∵BD∥CE,∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,∴CD=AB=BD,
∴四边形BECD是菱形;
21.(10分)
解:(1)设A系列产品的单价是x元/件,则B系列产品的单价是(x+5)元/件,
根据题意得:,解得:x=10,
经检验,x=10是所列方程的解,且符合题意,
∴x+5=10+5=15(元).
答:A系列产品的单价是10元/件,B系列产品的单价是15元/件;
(2)设B系列产品的实际售价应定为y元/件,则每天可以卖50+10(15﹣y)=(200﹣10y)件,
根据题意得:y(200﹣10y)=960,整理得:y2﹣20y+96=0,
解得:y1=8,y2=12,
又∵要尽可能让顾客得到实惠,∴y=8.
答:B系列产品的实际售价应定为8元/件.
22.(10分)解:(1)26,12;
(2)设剪去的正方形的边长为x cm,根据题意得:(30﹣2x)(16﹣2x)=240,
解得:x1=20(不符合题意,舍去),x2=3,
答:剪去的正方形的边长为3cm;
(3)设剪去的正方形的边长为y cm,根据题意得:,
解得:y1=﹣17(不符合题意,舍去),y2=2,
答:剪去的正方形的边长为2cm.
23.(12分)解:(1)CF+CE=BC;
(2)如图2,过点O′作O′G∥AB,交BC于G,
∵四边形ABCD和四边形A′B′C′O′是形状、大小完全相同的菱形,且边长为8,α=60°,
∴AB=BC=CD=AD=A′B′=B′C′=C′O′=O′A′=8,∠B=∠D=∠B′=∠A′O′C′=60°,
∴△ABC、△ACD均为等边三角形,
∴∠BAC=∠ACB=∠ACD=60°,AC=AB=8,
∵O′G∥AB,∴∠CO′G=∠BAC=60°=∠O′CG,
∴△O′CG是等边三角形,∴O′G=CG=O′C=k•AC=8k,
∵∠EO′G+∠CO′E=∠CO′E+∠CO′F′=60°,
∴∠EO′G=∠CO′F,∴△O′EG≌△O′FC(ASA),∴EG=CF,
∵CE+EG=CG,∴CE+CF=8k;
(3)连接BD交AC于O,
∵四边形ABCD是菱形,∴AC⊥BD,即∠BOC=90°,∴OC=AC=BC=4,
∴,∴,
当点O′在线段AO上时,如图2,过点O′作O′H⊥BC于H,
则O′C=OO′+OC=1+4=5,∴,
由(2)知:CE+CF=8k,∴CE+CF=8×=5,∵CF=,∴CE=5﹣=;
当点O′在线段OC上时,如图3,
则O′C=OC﹣OO′=4﹣1=3,∴,∴CE+CF=8×=3,∴CE=3﹣=;
综上所述,CE的长度为或.
一.选择题(共10小题,满分30分,每小题3分)
1.下列方程中,属于一元二次方程的是( )
A.B.C.D.
2.下列说法正确的是( )
A.对角线相等的四边形是矩形B.对角线互相垂直的四边形是菱形
C.对角线相等的平行四边形是矩形D.对角线互相平分的四边形是菱形
3.关于的方程的根的情况是( )
A.有两个相等的实数根B.有两个不相等的实数根
C.只有一个实数根D.无实数根
4.关于的方程是一元二次方程,则的值是( )
A.B.1C.D.0
5.如图,已知在平面直角坐标系中,四边形是菱形,其中点的坐标是,点的坐标是,点在轴上,则点的坐标是( )
A.B.C.D.
6.如图,矩形中,,在轴上.且点的横坐标为,若以点为圆心,对角线的长为半径作弧交轴的正半轴于,则点的坐标为( )
A.B.C.D.
7.如图,菱形的对角线交于点,点为的中点,连接.若,、则的长为( )
A.4B.3C.D.
8.摩拜共享单车计划2023年第三季度(8,9,10月)连续3个月对成都投放新型摩拜单车,计划8月投放3000台,第三季度共投放12000台,每月按相同的增长率投放,设增长率为,则可列方程( )
A.B.
C.D.
9.在长为30m,宽为20m的长方形田地中开辟三条入口宽度相等的道路,已知剩余田地的面积为,求道路的宽度设道路的宽度为,则可列方程( )
A.B.
C.D.
10.如图,正方形中,点为对角线的中点,矩形两边分别交、边于、两点,连接,下列结论正确的有( )个.
(1);
(2);
(3);
(4)若,则以为斜边的直角三角形面积的最大值为8.
A.1个B.2个C.3个D.4个
二.填空题(共5小题,满分15分,每小题3分)
11.关于的一元二次方程有实数根,则的取值范围是_________.
12.如图,在菱形中,,点、分别是线段、上的动点,连接、,若,,则图中阴影部分的面积是_________.
13.根据物理学规律,如果把一个物体从地面以的速度竖直上抛(如图所示),那么物体经过离地面的高度(单位:m)为.根据上述规律,该物体落回地面所需要的时间约为_________s(结果保留整数).
14.如图,菱形的对角线,相交于点,过点作于点,连接,若,菱形的面积为18,则_________.
15.如图,,,,,点为的中点,点在的延长线上,将绕点顺时针旋转度得到,当是直角三角形时,的长为_________.
三.解答题(共8小题,满分75分)
16.(8分)解方程:
(1);(2)
17.(8分)已知关于的一元二次方程.
(1)求证:该方程总有两个不相等的实数根;
(2)若是该方程的一个解,求方程的另一个根.
18.(10分)如图,在平面直角坐标系中,三个顶点的坐标分别为,,.
(1)画出将向左平移4个单位后得到的图形;
(2)画出将绕点按逆时针方向旋转后得到的图形,并直接写出四边形的形状;
(3)在平面内有一点,当以,,,为顶点的四边形是平行四边形时,请直接写出点的坐标.
19.(8分)如图,在平行四边形中,是上一点(不与点,重合),,过点作,交于点,连接,.
(1)求证:四边形是矩形;
(2)当,时,求的长.
20.(9分)如图,在中,,过点的直线,为边上点,过点作交直线与,垂足为,连接,.
(1)求证:;
(2)当在中点时,四边形是什么特殊四边形?说明理由;
21.(10分)三星堆遗址被称为20世纪人类最伟大的考古发现之一,昭示了长江流域与黄河流域一样,同属中华文明的母体,被誉为“长江文明之源”.为更好的传承和宣传三星堆文化,三星堆文创馆一次次打破了自身限定,让文创产品充满创意.已知文创产品“青铜鸟文创水杯”有,两个系列,系列产品比系列产品的售价低5元,100元购买系列产品的数量与150元购买系列产品的数量相等.按定价销售一段时间后发现:系列产品按定价销售,每天可以卖50件,若系列产品每降1元,则每天可以多卖10件.
(1)系列产品和系列产品的单价各是多少?
(2)为了使系列产品每天的销售额为960元,而且尽可能让顾客得到实惠,求系列产品的实际售价应定为多少元/件?
22.(10分)综合实践——用矩形硬纸片制作无盖纸盒.如图1,有一张长30cm,宽16cm的长方形硬纸片,裁去角上同样大小的四个小正方形之后,折成图2所示的无盖纸盒.(硬纸片厚度忽略不计)
(1)若剪去的正方形的边长为2cm,则纸盒底面长方形的长为_________cm,宽为_________cm;
(2)若纸盒的底面积为,请计算剪去的正方形的边长;
(3)如图3,小明先在原矩形硬纸片的两个角各剪去一个同样大小的正方形(阴影部分),经过思考他发现,再剪去两个同样大小的矩形后,可将剩余部分折成一个有盖纸盒.若折成的有盖长方体纸盒的表面积为,请计算剪去的正方形的边长.
23.(12分)在菱形中,,点在对角线上运动(点不与点,点重合),,以点为顶点作菱形;且菱形与菱形的形状、大小完全相同,即,,在菱形绕点旋转的过程中,与边交于点,与边交于点.
【特例感知】
(1)如图1,当,时,则,,之间满足的数量关系是_________;
【类比探究】
(2)如图2,菱形的边长为8,,求的值(用含的代数式表示);
【拓展应用】
(3)在(2)的条件下,连接,,,求的长度.
九上数学北师大(一)
参考答案与试题解析
一.选择题
1-5.DCABC. 6-10. CCDAB.
二.填空题
11. a≤14且a≠0. 12. 13. 2. 14.2. 15. 5或35.
三.解答题(共8小题,满分75分)
16.(8分)(每题4分)
解:(1)x2﹣6x+8=0,
因式分解得,(x﹣2)(x﹣4)=0,x﹣2=0,x﹣4=0,
解得,x1=4,x2=2;
(2)x2﹣3x+1=0
∵a=1,b=﹣3,c=1,∴b2﹣4ac=(﹣3)2﹣4×1×1=5>0,
∴,
∴,.
17.(8分)(1)证明:∵在一元二次方程x2+(n+2)x+n=0中,a=1,b=n+2,c=n,
∴Δ=b2﹣4ac=(n+2)2﹣4n=n2+4>0,
∴方程总有两个不相等的实数根.
(2)解:∵x=﹣2是该方程的一个解,
∴(﹣2)2﹣2(n+2)+n=0,解得n=0,
∴该方程为x2+2x=0,解得x1=﹣2,x2=0,∴方程的另一个根为x=0.
18.(10分)
【解答】解:(1)如图,△A1B1C1即为所求.3分
(2)如图,△A2B2C即为所求. 5分
由旋转得,BC=B2C,AC=A2C,∴四边形A2B2AB为平行四边形.
(3)如图,点D1,D2,D3均满足题意,
∴满足题意的点D的坐标为(2,4)或(4,0)或(﹣2,﹣2).
19.(8分)(1)证明:∵∠BPQ=∠BPC+∠CPQ=∠A+∠AQP,∠BPC=∠AQP,
∴∠CPQ=∠A,
∵PQ⊥CP,∴∠A=∠CPQ=90°,∴平行四边形ABCD是矩形;
(2)解:∵四边形ABCD是矩形,
∴∠D=∠CPQ=90°,
在Rt△CDQ和Rt△CPQ中,,
∴Rt△CDQ≌Rt△CPQ(HL),∴DQ=PQ,
设AQ=x,则DQ=PQ=9﹣x,
在Rt△APQ中,AQ2+AP2=PQ2,∴x2+32=(9﹣x)2,解得:x=4,
∴AQ的长是4.
20.(9分)(1)证明:∵DE⊥BC,∴∠DFB=90°,
∵∠ACB=90°,∴∠ACB=∠DFB,∴AC∥DE,
∵MN∥AB,即CE∥AD,∴四边形ADEC是平行四边形,∴CE=AD;
(2)解:四边形BECD是菱形,理由如下:
∵D为AB中点,∴AD=BD,∵CE=AD,∴BD=CE,
∵BD∥CE,∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,∴CD=AB=BD,
∴四边形BECD是菱形;
21.(10分)
解:(1)设A系列产品的单价是x元/件,则B系列产品的单价是(x+5)元/件,
根据题意得:,解得:x=10,
经检验,x=10是所列方程的解,且符合题意,
∴x+5=10+5=15(元).
答:A系列产品的单价是10元/件,B系列产品的单价是15元/件;
(2)设B系列产品的实际售价应定为y元/件,则每天可以卖50+10(15﹣y)=(200﹣10y)件,
根据题意得:y(200﹣10y)=960,整理得:y2﹣20y+96=0,
解得:y1=8,y2=12,
又∵要尽可能让顾客得到实惠,∴y=8.
答:B系列产品的实际售价应定为8元/件.
22.(10分)解:(1)26,12;
(2)设剪去的正方形的边长为x cm,根据题意得:(30﹣2x)(16﹣2x)=240,
解得:x1=20(不符合题意,舍去),x2=3,
答:剪去的正方形的边长为3cm;
(3)设剪去的正方形的边长为y cm,根据题意得:,
解得:y1=﹣17(不符合题意,舍去),y2=2,
答:剪去的正方形的边长为2cm.
23.(12分)解:(1)CF+CE=BC;
(2)如图2,过点O′作O′G∥AB,交BC于G,
∵四边形ABCD和四边形A′B′C′O′是形状、大小完全相同的菱形,且边长为8,α=60°,
∴AB=BC=CD=AD=A′B′=B′C′=C′O′=O′A′=8,∠B=∠D=∠B′=∠A′O′C′=60°,
∴△ABC、△ACD均为等边三角形,
∴∠BAC=∠ACB=∠ACD=60°,AC=AB=8,
∵O′G∥AB,∴∠CO′G=∠BAC=60°=∠O′CG,
∴△O′CG是等边三角形,∴O′G=CG=O′C=k•AC=8k,
∵∠EO′G+∠CO′E=∠CO′E+∠CO′F′=60°,
∴∠EO′G=∠CO′F,∴△O′EG≌△O′FC(ASA),∴EG=CF,
∵CE+EG=CG,∴CE+CF=8k;
(3)连接BD交AC于O,
∵四边形ABCD是菱形,∴AC⊥BD,即∠BOC=90°,∴OC=AC=BC=4,
∴,∴,
当点O′在线段AO上时,如图2,过点O′作O′H⊥BC于H,
则O′C=OO′+OC=1+4=5,∴,
由(2)知:CE+CF=8k,∴CE+CF=8×=5,∵CF=,∴CE=5﹣=;
当点O′在线段OC上时,如图3,
则O′C=OC﹣OO′=4﹣1=3,∴,∴CE+CF=8×=3,∴CE=3﹣=;
综上所述,CE的长度为或.












