期中复习 七年级数学相交线与平行线基础解答题及解析 典例例题总结试卷

这是一份期中复习 七年级数学相交线与平行线基础解答题及解析 典例例题总结试卷，共67页。试卷主要包含了看图填空等内容，欢迎下载使用。

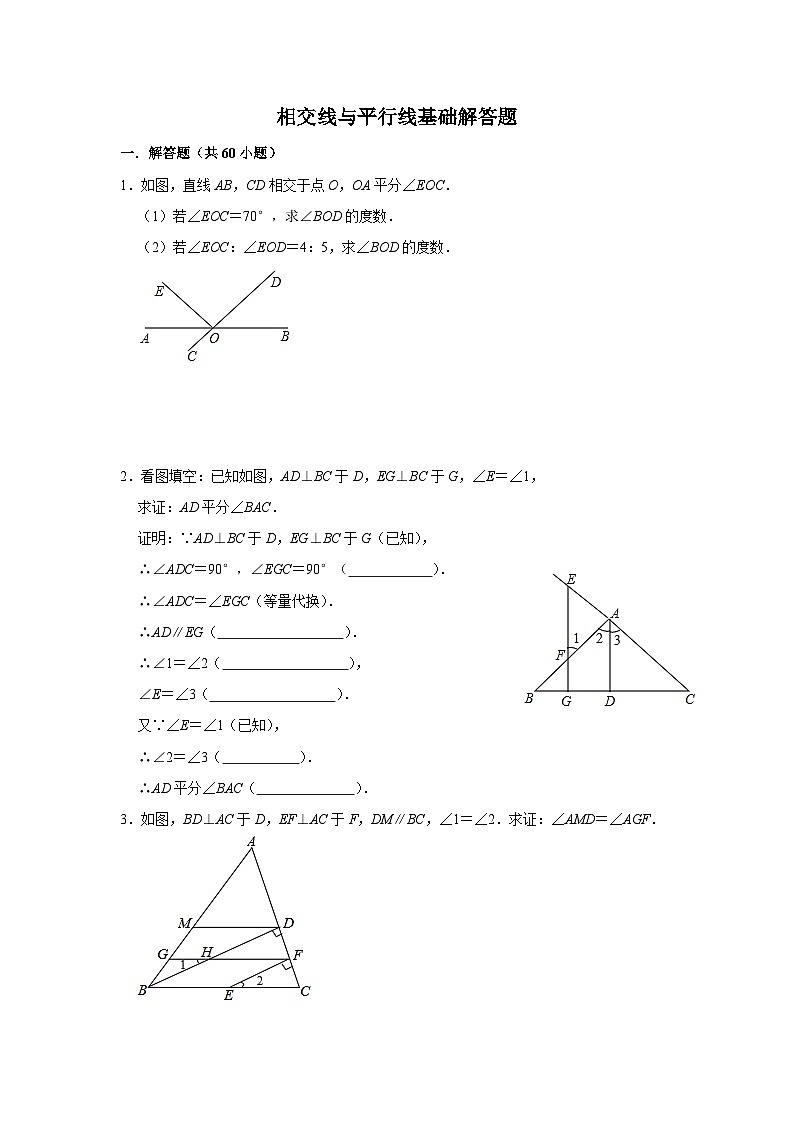
1．如图，直线AB，CD相交于点O，OA平分∠EOC．
（1）若∠EOC＝70°，求∠BOD的度数．
（2）若∠EOC：∠EOD＝4：5，求∠BOD的度数．
2．看图填空：已知如图，AD⊥BC于D，EG⊥BC于G，∠E＝∠1，
求证：AD平分∠BAC．
证明：∵AD⊥BC于D，EG⊥BC于G（已知），
∴∠ADC＝90°，∠EGC＝90°（ ）．
∴∠ADC＝∠EGC（等量代换）．
∴AD∥EG（ ）．
∴∠1＝∠2（ ），
∠E＝∠3（ ）．
又∵∠E＝∠1（已知），
∴∠2＝∠3（ ）．
∴AD平分∠BAC（ ）．
3．如图，BD⊥AC于D，EF⊥AC于F，DM∥BC，∠1＝∠2．求证：∠AMD＝∠AGF．
4．阅读理解填空，并在括号内填注理由．
如图，已知AB∥CD，M，N分别交AB，CD于点E，F，∠1＝∠2，求证：EP∥FQ．
证明：∵AB∥CD（ ）
∴∠MEB＝∠MFD（ ）．
又∵∠1＝∠2（ ）
∠MEB﹣∠1＝∠MFD﹣∠2（ ）
即：∠MEP＝∠
EP∥ ．（ ）
5．如图，直线AB，CD相交于点O，OE平分∠BOC，∠FOD＝90°
（1）若∠AOF＝50°，求∠BOE的度数；
（2）若∠BOD：∠BOE＝1：4，求∠AOF的度数．
6．如图，已知∠1+∠2＝180°，∠B＝∠3，判断∠C与∠AED的大小关系，并说明理由．
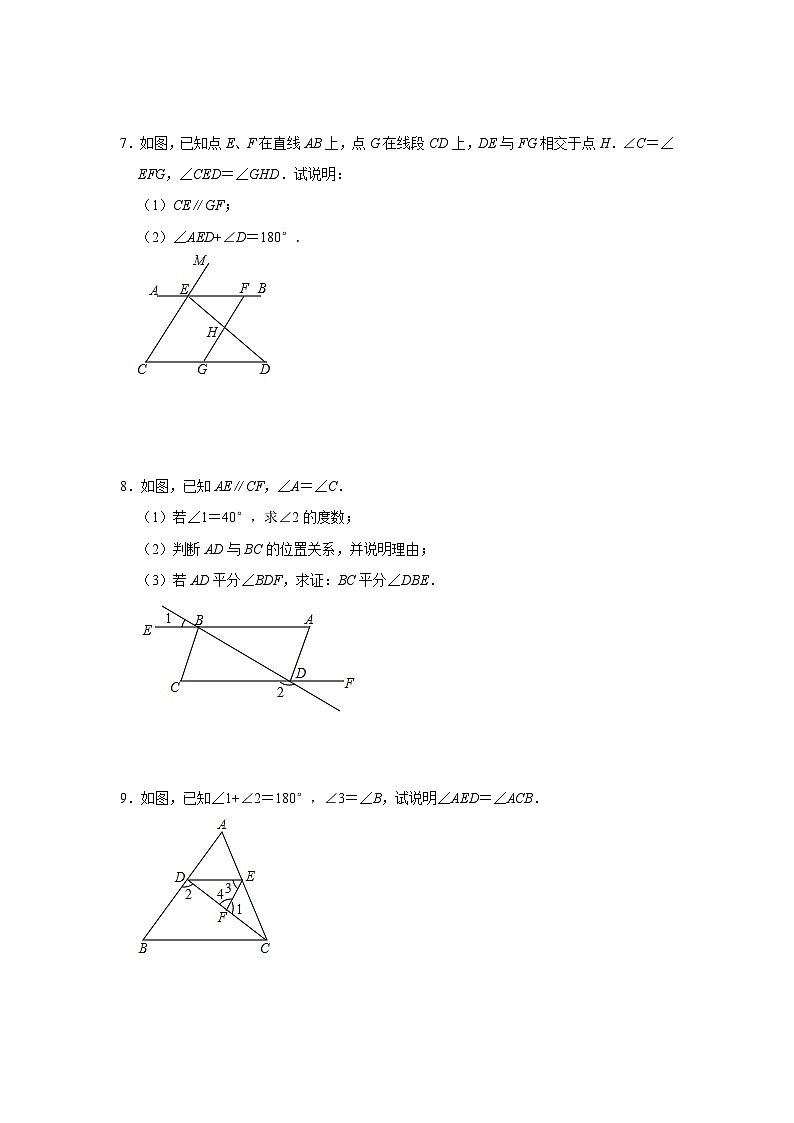
7．如图，已知点E、F在直线AB上，点G在线段CD上，DE与FG相交于点H．∠C＝∠EFG，∠CED＝∠GHD．试说明：
（1）CE∥GF；
（2）∠AED+∠D＝180°．
8．如图，已知AE∥CF，∠A＝∠C．
（1）若∠1＝40°，求∠2的度数；
（2）判断AD与BC的位置关系，并说明理由；
（3）若AD平分∠BDF，求证：BC平分∠DBE．
9．如图，已知∠1+∠2＝180°，∠3＝∠B，试说明∠AED＝∠ACB．
10．已知如图，△ABC过点A作∠DAE＝∠BAC，且AD∥BC，∠1＝∠2．
（1）求证AB∥DE；
（2）若已知AE平分∠BAC，∠C＝35°，求∠BAD的度数．
11．如图，AB交CD于O，OE⊥AB．
（1）若∠EOD＝20°，求∠AOC的度数；
（2）若∠AOC：∠BOC＝1：2，求∠EOD的度数．
12．完成正确的证明如图，已知AB∥CD，求证：∠BED＝∠B+∠D
证明：过E点作EF∥AB
∴∠1＝
∵AB∥CD（已知）
∴EF∥CD（ ）
∴∠2＝
又∠BED＝∠1+∠2
∴∠BED＝∠B+∠D （ ）．
13．如图，在△ABC中，CD⊥AB于D，FG⊥AB于G，ED∥BC，
求证：∠1＝∠2．
14．完成下面的推理填空：
如图，已知AB∥CD，∠1＝∠2，∠3＝∠4，求证：∠D＝∠DCE．
证明：∵AB∥CD，
∴∠2＝∠BAE（ ）．
∵∠BAE＝∠3+ ，
∴∠2＝∠3+ ，
∵∠3＝∠4，
∴∠2＝∠CAD，
又∵∠2＝ ，
∴∠CAD＝ ，
∴AD∥ （ ）．
∴∠D＝∠DCE．（ ）．
15．如图，已知，F是DG上的点，∠1+∠2＝180°，∠3＝∠B，求证：∠AED＝∠C．
证明：∵F是DG上的点（已知）
∴∠2+∠DFE＝180° （ ）
又∵∠1+∠2＝180°（已知）
∴∠1＝∠DFE （ ）
∴BD∥EF （ ）
∴∠3＝∠ADE （ ）
又∵∠3＝∠B（已知）
∴∠B＝∠ADE （ ）
∴DE∥BC （ ）
∴∠AED＝∠C （ ）
16．如图，点F在线段AB上，点E、G在线段CD上，AB∥CD．
（1）若BC平分∠ABD，∠D＝100°，求∠ABC的度数．
解：∵AB∥CD（已知），
∴∠ABD+∠D＝180°，（ ）
∵∠D＝100°，（已知）
∴∠ABD＝ °，
∵BC平分∠ABD，（已知）
∴∠ABC＝∠ABD＝40°．（角平分线的定义）
（2）若∠1＝∠2，求证：AE∥FG．
17．完成下面的推理填空：
已知：如图，E、F分别在AB和CD上，∠1＝∠D，∠2与∠C互余，AF⊥CE于G．
求证：AB∥CD．
证明：∵AF⊥CE
∴∠CGF＝90°
∵∠1＝∠D（已知）
∴ ∥ （ ）
∴∠4＝∠CGF＝90° （ ）
又∵∠2与∠C互余（已知），∠2+∠3+∠4＝180°
∴∠2+∠C＝∠2+ ＝90°
∴∠C＝
∴AB∥CD．
18．如图，AB交CD于O，OE⊥AB．（1）若∠EOD＝20°，求∠AOC的度数；
（2）若∠AOC：∠BOC＝1：2，求∠EOD的度数．
19．如图，已知∠ABC＝180°﹣∠A，BD⊥CD于D，EF⊥CD于E．
（1）求证：AD∥BC；
（2）若∠ADB＝36°，求∠EFC的度数．
20．阅读下列文字，并完成证明；
已知：如图，∠1＝∠4，∠2＝∠3，求证：AB∥CD；
证明：如图，延长CF交AB于点G
∵∠2＝∠3
∴BE∥CF（ ）
∴∠1＝ （两直线平行，同位角相等）
又∠1＝∠4
∴∠AGF＝ （ ）
∴AB∥CD（内错角相等，两直线平行）
21．如图，点B，E分别在AC，DF上，BD，CE均与AF相交，∠A＝∠F，∠C＝∠D，求证：∠1＝∠2．
22．已知：如图EF∥CD，∠1+∠2＝180°．
（1）试说明GD∥CA；
（2）若CD平分∠ACB，DG平分∠CDB，且∠A＝40°，求∠ACB的度数．
23．如图，在三角形ABC中，点D、G分别为边BC、AB上的点，DE⊥AC于点E，BF⊥AC于点F，连接FG，且∠BFG+∠BDE＝180°．
（1）求证：DE∥BF；
（2）猜想∠AGF与∠ABC的数量关系，并证明你的猜想．
24．已知：如图，AE⊥BC，FG⊥BC，∠1＝∠2
（1）求证：AB∥CD
（2）若∠D＝∠3+50°，∠CBD＝70°，求∠C的度数．
25．如图，在三角形ABC中，D，E，F分别是三边上的点，且DE平分∠ADF，∠ADF＝2∠DFB．
（1）判断DE与BC是否平行，并说明理由．
（2）若EF∥AB，∠DFE＝3∠CFE，求∠ADE的度数．
26．如图，AB∥CD，AE平分∠BAD，CD与AE相交于F，∠CFE＝∠E．求证：AD∥BC．
27．完成下面的推理，并在括号内标注理由：
如图，∠DEH+∠EHG＝180°，∠1＝∠2，∠C＝∠A．
求证：∠AEH＝∠F．
证明：∵∠DEH+∠EHG＝180°，
∴ED∥ （ ）．
∴∠1＝∠C（ ）．
∠2＝ （ ）．
∵∠1＝∠2，∠C＝∠A（ ），
∴∠A＝ ．
∴AB∥DF（ ）．
∴∠AEH＝∠F（ ）．
28．如图，∠BAP+∠APD＝180°，∠1＝∠2，求证：∠E＝∠F．
29．如图，CD⊥AB于D，点F是BC上任意一点，FE⊥AB于E，且∠1＝∠2，∠3＝80°．
（1）试证明∠B＝∠ADG；
（2）求∠BCA的度数．
30．如图，EF∥AD，∠1＝∠2，∠BAC＝80°．将求∠AGD的过程填写完整．
因为EF∥AD，
所以∠2＝ （ ），
又因为∠1＝∠2，
所以∠1＝∠3（ ），
所以AB∥ （ ），
所以∠BAC+ ＝180°（ ），
因为∠BAC＝80°，
所以∠AGD＝ ．
31．请补全证明过程及推理依据．
已知：如图，BC∥ED，BD平分∠ABC，EF平分∠AED．
求证：BD∥EF．
证明：∵BD平分∠ABC，EF平分∠AED，
∴∠1＝∠AED，∠2＝∠ABC（ ）．
∵BC∥ED，
∴∠AED＝ （ ）
∴∠AED＝∠ABC．
∴∠1＝∠2（ ）．
∴BD∥EF（ ）．
32．已知：如图，点D、E、G分别是△ABC边BC、AB和AC上的点，AD∥EF，点F在BC上，∠1＝∠2＝∠B．
求证：①AB∥DG；
②DG平分∠ADC．
33．如图，已知AD⊥BC，EF⊥BC，垂足分别为D、F，∠2+∠3＝180°，试说明：∠GDC＝∠B．请补充说明过程，并在括号内填上相应的理由．
解：∵AD⊥BC，EF⊥BC（已知）
∴∠ADB＝∠EFB＝90° （ ），
∴EF∥AD（ ），
∴ +∠2＝180°（ ）．
又∵∠2+∠3＝180°（已知），
∴∠1＝∠3（ ），
∴AB∥ （ ），
∴∠GDC＝∠B（ ）．
34．如图，BD平分∠ABC，F在AB上，G在AC上，FC与BD相交于点H，∠3+∠4＝180°，试说明∠1＝∠2．（请通过填空完善下列推理过程）
解：∵∠3+∠4＝180°（已知），∠FHD＝∠4（ ）．
∴∠3+ ＝180°（等量代换）．
∴FG∥BD（ ）．
∴∠1＝ （ ）．
∵BD平分∠ABC，
∴∠ABD＝ （ ）．
∴∠1＝∠2（ ）．
35．如图，D，E分别在△ABC的边AB，AC上，F在线段CD上，且∠1+∠2＝180°，DE∥BC．
（1）求证：∠3＝∠B；
（2）若DE平分∠ADC，∠2＝3∠B，求∠1的度数．
36．请根据条件进行推理，得出结论，并在括号内注明理由．
已知：如图，BD⊥AC，EF⊥AC，∠1+∠2＝180°．
求证：DG∥BC．
证明：∵BD⊥AC，EF⊥AC（已知），
∴∠BDC＝∠EFC＝90°（垂直的定义）．
∴ ∥ （ ）．
∴∠2+ ＝180°（ ）．
又∵∠1+∠2＝180°（已知），
∴∠1＝ （ ）．
∴DG∥BC（ ）．
37．如图，已知AB∥CD，∠1＝∠2，求证：BE∥GF．
38．完成下列推理说明：
（1）如图1，已知∠1＝∠2，∠B＝∠C，可推出AB∥CD．理由如下：
因为∠1＝∠2（已知），且∠1＝∠4（ ）
所以∠2＝∠4（等量代换）
所以CE∥BF（ ）
所以∠ ＝∠3（ ）
又因为∠B＝∠C（已知）
所以∠3＝∠B（等量代换）
所以AB∥CD（ ）
（2）如图2，已知∠B+∠BCD＝180°，∠B＝∠D．求证：∠E＝∠DFE．
证明：∵∠B+∠BCD＝180°（ 已知 ），
∴AB∥CD （ ）
∴∠B＝ （ ）
又∵∠B＝∠D（ 已知 ），
∴∠ ＝∠ （等量代换）
∴AD∥BE（ ）
∴∠E＝∠DFE（ ）
39．如图，已知AB∥CD，∠1＝∠2，CF平分∠DCE．
（1）试判断直线AE与BF有怎样的位置关系？并说明理由；
（2）若∠1＝80°，求∠3的度数．
40．阅读下列推理过程，在括号中填写理由．
已知：如图，点D、E分别在线段AB、BC上，AC∥DE，DF∥AE交BC于点F，AE平分∠BAC．求证：DF平分∠BDE
证明：∵AE平分∠BAC（已知）
∴∠1＝∠2（ ）
∵AC∥DE（已知）
∴∠1＝∠3（ ）
故∠2＝∠3（ ）
∵DF∥AE（已知）
∴∠2＝∠5，（ ）
∠3＝∠4（ ）
∴∠4＝∠5（ ）
∴DF平分∠BDE（ ）
41．如图，点D、F在线段AB上，点E、G分别在线段BC和AC上，CD∥EF，∠1＝∠2．
（1）判断DG与BC的位置关系，并说明理由；
（2）若DG是∠ADC的平分线，∠3＝85°，且∠DCE：∠DCG＝9：10，试说明AB与CD有怎样的位置关系？
42．如图，点D、E、F、G均在△ABC的边上，连接BD、DE、FG，∠3＝∠CBA，FG∥BD．
（1）求证：∠1+∠2＝180°；
（2）若BD平分∠CBA，DE平分∠BDC，∠A＝35°，求∠C的度数．
43．已知：如图，∠B＝∠ADE，∠EDC＝∠GFB，GF⊥AB．
求证：CD⊥AB．
44．已知：如图，AD⊥BC于D，EG⊥BC于G，∠E＝∠AFE．
求证：AD平分∠BAC．
45．已知：如图，∠1＝∠2，∠B+∠CDE＝180°．
求证：AB∥CD．
证明：∵∠1＝ （ ），
又∵∠1＝∠2，
∴∠BFD＝∠2 （ ）．
∴BC∥ （ ）．
∴∠C+ ＝180° （ ）．
又∵∠B+∠CDE＝180°，
∴∠B＝∠C．
∴AB∥CD （ ）．
46．已知，如图，∠ABC＝∠ADC，BF、DE分别平分∠ABC与∠ADC，且∠1＝∠3．求证：AB∥DC．请根据条件进行推理，得出结论，并在括号内注明理由．
证明：∵BF、DE分别平分∠ABC与∠ADC，
∴∠1＝∠ABC，∠2＝．（ ）
∵∠ABC＝∠ADC，
∵∠ ＝∠ ．
∵∠1＝∠3，
∴∠2＝ ．（等量代换）
∴ ∥ ．（ ）
47．如图AB∥CD，点P是平面内直线AB、CD外一点连接PA、PC．
（1）写出所给的四个图形中∠APC、∠PAB、∠PCD之间的数量关系；
（2）证明图（1）和图（3）的结论．
48．如图，直线AB，CD相交于点O，OE平分∠BOC，OF⊥CD．
（1）若∠AOF＝50°，求∠BOE的度数；
（2）若∠BOD：∠BOE＝1：4，求∠AOF的度数．
49．如图，已知∠1＝∠2＝52°，EF∥DB．
（1）DG与AB平行吗？请说明理由；
（2）若EC平分∠FED，求∠C的度数．
50．如图，已知DG∥BA，∠1＝∠2，求证：AD∥EF．
51．如图，已知AD∥CB，∠A＝∠C，若∠ABD＝32°，求∠BDC的度数．有同学用了下面的方法．但由于一时犯急没有写完整，请你帮他添写完整．
解：∵AD∥CB（ 已知 ）
∴∠C+∠ADC＝180° （ ）
又∵∠A＝∠C （ ）
∴∠A+∠ADC＝180° （ ）
∴AB∥CD （ ）
∴∠BDC＝∠ABD＝32° （ ）．
52．填空，将理由补充完整
已知：如图，AB∥CD，∠B＝∠D，直线EF与AD，BC的延长线分别交于点E，F，
求证：∠DEF＝∠F．
证明：∵AB∥CD（已知），
∴∠B＝ （ ），
∵∠B＝∠D（ ），
∴∠D＝ （ ），
∴AD∥ （ ），
∴∠DEF＝∠F（ ）．
53．如图，∠AGF＝∠ABC，∠1+∠2＝180°．
（1）求证：BF∥DE；
（2）若DE⊥AC，∠2＝144°，求∠AFG的度数．
54．已知AD⊥BC于D，FG⊥BC垂足分别为D，G，且∠1＝∠2，∠C＝50°，求∠EDC的度数．
证明：∵AD⊥BC，FG⊥BC，
∴∠ADC＝ ，∠FGC＝90°（ ）．
∴ ∥FG（ ）．
∴∠1＝∠3
又∵∠1＝∠2，
∴∠2＝∠3（ ）．
∴DE∥ ．
∴∠EDC+∠C＝180°（ ）．
∵∠C＝50°．
∴∠EDC＝ °．
55．如图，∠1+∠2＝180°，∠3＝100°，OK平分∠DOH，求∠KOH的度数．
证明：∵∠1+∠2＝180°，
∴AB∥CD（ ）．
∴∠3＝∠4（ ）．
∵∠3＝100°，
∴∠4＝100°．
∴∠DOH＝180°﹣∠4＝80°．
∵OK平分∠DOH，
∴∠KOH＝∠DOH＝ （ ）．
56．如图，∠1+∠2＝180°，∠DEF＝∠A，∠BED＝70°．
（1）求证：EF∥AB；
（2）求∠ACB的度数．
57．如图，AB∥CD，直线EF分别交直线AB、CD于点M、N，MG平分∠EMB，NH平分∠CNF，求证：MG∥NH．
58．已知：如图，∠DAB＝∠DCB，AF平分∠DAB，CE平分∠DCB，∠FCE＝∠CEB．试说明：AF∥CE．
解：因为∠DAB＝∠DCB（ ），
又因为AF平分∠DAB，
所以 ＝∠DAB（ ）．
又因为CE平分∠DCB，
所以∠FCE＝ （ ）．
所以∠FAE＝∠FCE．
因为∠FCE＝∠CEB，
所以 ＝ ．
所以AF∥CE（ ）．
59．完成下列证明：如图，已知AD⊥BC，EF⊥BC，∠1＝∠2．
求证：∠BAC+∠AGD＝180°．
证明：∵AD⊥BC，EF⊥BC（已知），
∴∠EFB＝90°，∠ADB＝90°（ ），
∴∠EFB＝∠ADB（等量代换），
∴EF∥AD（ ），
∴∠1＝∠BAD（ ），
又∵∠1＝∠2（已知），
∴∠ ＝∠ （等量代换），
∴DG∥BA（ ），
∴∠BAC+∠AGD＝180°（ ）．
60．如图，已知∠1＝∠BDC，∠2+∠3＝180°．
（1）请你判断DA与CE的位置关系，并说明理由；
（2）若DA平分∠BDC，CE⊥AE于E，∠1＝70°，试求∠FAB的度数．
相交线与平行线基础解答题
参考答案与试题解析
一．解答题（共60小题）
1．如图，直线AB，CD相交于点O，OA平分∠EOC．
（1）若∠EOC＝70°，求∠BOD的度数．
（2）若∠EOC：∠EOD＝4：5，求∠BOD的度数．
【解答】解：（1）∵∠EOC＝70°，OA平分∠EOC，
∴∠AOC＝35°，
∴∠BOD＝∠AOC＝35°；
（2）设∠EOC＝4x，则∠EOD＝5x，
∴5x+4x＝180°，
解得x＝20°，
则∠EOC＝80°，
又∵OA平分∠EOC，
∴∠AOC＝40°，
∴∠BOD＝∠AOC＝40°．
2．看图填空：已知如图，AD⊥BC于D，EG⊥BC于G，∠E＝∠1，
求证：AD平分∠BAC．
证明：∵AD⊥BC于D，EG⊥BC于G（已知），
∴∠ADC＝90°，∠EGC＝90°（ 垂直的定义 ）．
∴∠ADC＝∠EGC（等量代换）．
∴AD∥EG（ 同位角相等，两直线平行 ）．
∴∠1＝∠2（ 两直线平行，内错角相等 ），
∠E＝∠3（ 两直线平行，同位角相等 ）．
又∵∠E＝∠1（已知），
∴∠2＝∠3（ 等量代换 ）．
∴AD平分∠BAC（ 角平分线的定义 ）．
【解答】证明：
∵AD⊥BC于D，EG⊥BC于G（已知），
∴∠ADC＝90°，∠EGC＝90°（垂直的定义），
∴∠ADC＝∠EGC（等量代换），
∴AD∥EG（同位角相等，两直线平行 ），
∴∠1＝∠2（两直线平行，内错角相等），
∠E＝∠3（两直线平行，同位角相等），
又∵∠E＝∠1（ 已知），
∴∠2＝∠3（等量代换），
∴AD平分∠BAC（角平分线的定义）．
故答案为：垂直的定义；同位角相等，两直线平行；两直线平行，内错角相等；两直线平行，同位角相等；等量代换；角平分线的定义．
3．如图，BD⊥AC于D，EF⊥AC于F，DM∥BC，∠1＝∠2．求证：∠AMD＝∠AGF．
【解答】证明：∵BD⊥AC，EF⊥AC，
∴BD∥EF，
∴∠2＝∠CBD，
∵∠2＝∠1，
∴∠1＝∠CBD，
∴GF∥BC，
∵BC∥DM，
∴MD∥GF，
∴∠AMD＝∠AGF．
4．阅读理解填空，并在括号内填注理由．
如图，已知AB∥CD，M，N分别交AB，CD于点E，F，∠1＝∠2，求证：EP∥FQ．
证明：∵AB∥CD（ 已知 ）
∴∠MEB＝∠MFD（ 两直线平行同位角相等 ）．
又∵∠1＝∠2（ 已知 ）
∠MEB﹣∠1＝∠MFD﹣∠2（ 角的和差定义 ）
即：∠MEP＝∠ MFQ
EP∥ FQ ．（ 同位角相等两直线平行 ）
【解答】证明：∵AB∥CD（已知）
∴∠MEB＝∠MFD（两直线平行同位角相等）．
又∵∠1＝∠2（已知）
∠MEB﹣∠1＝∠MFD﹣∠2（角的和差定义）
即：∠MEP＝∠MFQ
EP∥FQ．（同位角相等两直线平行）
故答案为：已知，两直线平行同位角相等，已知，角的和差定义，MFQ，FQ，同位角相等两直线平行．
5．如图，直线AB，CD相交于点O，OE平分∠BOC，∠FOD＝90°
（1）若∠AOF＝50°，求∠BOE的度数；
（2）若∠BOD：∠BOE＝1：4，求∠AOF的度数．
【解答】解：（1）∵∠COF与∠DOF是邻补角，
∴∠COF＝180°﹣∠DOF＝90°．
∵∠AOC与∠AOF互为余角，
∴∠AOC＝90°﹣∠AOF＝90°﹣50°＝40°．
∵∠AOC与∠BOC是邻补角，
∴∠COB＝180°﹣∠AOC＝180°﹣40°＝140°．
∵OE平分∠BOC，
∴∠BOE＝∠BOC＝70°；
（2）∠BOD：∠BOE＝1：4，
设∠BOD＝∠AOC＝x，∠BOE＝∠COE＝4x．
∵∠AOC与∠BOC是邻补角，
∴∠AOC+∠BOC＝180°，
即x+4x+4x＝180°，
解得x＝20°．
∵∠AOC与∠AOF互为余角，
∴∠AOF＝90°﹣∠AOC＝90°﹣20°＝70°．
6．如图，已知∠1+∠2＝180°，∠B＝∠3，判断∠C与∠AED的大小关系，并说明理由．
【解答】解：∠C＝∠AED，理由是：
∵∠1+∠2＝180°，∠1+∠EFD＝180°，
∴∠2＝∠EFD，
∴AB∥EF，
∴∠3＝∠ADE，
∵∠B＝∠3，
∴∠ADE＝∠B，
∴DE∥BC，
∴∠C＝∠AED．
7．如图，已知点E、F在直线AB上，点G在线段CD上，DE与FG相交于点H．∠C＝∠EFG，∠CED＝∠GHD．试说明：
（1）CE∥GF；
（2）∠AED+∠D＝180°．
【解答】（1）证明：∵∠CED＝∠GHD，
∴CE∥GF；
（2）∵CE∥GF，
∴∠C＝∠FGD，
∵∠C＝∠EFG，
∴∠FGD＝∠EFG，
∴AB∥CD，
∴∠AED+∠D＝180°；
8．如图，已知AE∥CF，∠A＝∠C．
（1）若∠1＝40°，求∠2的度数；
（2）判断AD与BC的位置关系，并说明理由；
（3）若AD平分∠BDF，求证：BC平分∠DBE．
【解答】（1）解：∵AE∥CF，∠1＝40°，
∴∠BDC＝∠1＝40°，
又∵∠2+∠BDC＝180°，
∴∠2＝180°﹣∠BDC＝180°﹣40°＝140°；
（2）解：结论：BC∥AD．
理由：∵AE∥CF，
∴∠A+∠ADC＝180°，
又∵∠A＝∠C，
∴∠C+∠ADC＝180°，
∴BC∥AD．
（3）证明：∵AE∥CF，
∴∠BDF＝∠DBE．
∵BC∥AD，
∴∠ADB＝∠DBC．
∵AD平分∠BDF，
∴∠ADB＝∠BDF，
∴∠DBC＝∠EBD．
∴BC平分∠DBE．
9．如图，已知∠1+∠2＝180°，∠3＝∠B，试说明∠AED＝∠ACB．
【解答】证明：∵∠1+∠4＝180°（平角定义），∠1+∠2＝180°（已知），
∴∠2＝∠4，
∴EF∥AB（内错角相等，两直线平行），
∴∠3＝∠ADE（两直线平行，内错角相等），
∵∠3＝∠B（已知），
∴∠B＝∠ADE（等量代换），
∴DE∥BC（同位角相等，两直线平行），
∴∠AED＝∠ACB（两直线平行，同位角相等）．
10．已知如图，△ABC过点A作∠DAE＝∠BAC，且AD∥BC，∠1＝∠2．
（1）求证AB∥DE；
（2）若已知AE平分∠BAC，∠C＝35°，求∠BAD的度数．
【解答】（1）证明：∵AD∥BC，
∴∠DAE＝∠2，
∵∠1＝∠2，
∴∠DAE＝∠1，
∵∠DAE＝∠BAC，
∴∠BAC＝∠1，
∴AB∥DE；
（2）解：∵∠DAE＝∠BEA，
∴∠BAE＝∠EAC＝∠DAC，
∵AD∥BC，
∴∠C＝∠DAC，
∴∠C＝∠BAE＝∠DAC＝35°，
∵AE平分∠BAC，
∴∠BAC＝2∠BAE＝70°，
∴∠BAD＝∠BAC+∠CAD＝105°．
11．如图，AB交CD于O，OE⊥AB．
（1）若∠EOD＝20°，求∠AOC的度数；
（2）若∠AOC：∠BOC＝1：2，求∠EOD的度数．
【解答】解：（1）∵OE⊥AB，
∴∠AOE＝90°，
∵∠EOD＝20°，
∴∠AOC＝180°﹣90°﹣20°＝70°；
（2）设∠AOC＝x，则∠BOC＝2x，
∵∠AOC+∠BOC＝180°，
∴x+2x＝180°，
解得：x＝60°，
∴∠AOC＝60°，
∴∠BOD＝60°，
∴∠EOD＝180°﹣90°﹣60°＝30°．
12．完成正确的证明如图，已知AB∥CD，求证：∠BED＝∠B+∠D
证明：过E点作EF∥AB
∴∠1＝ ∠B
∵AB∥CD（已知）
∴EF∥CD（ 如果两条直线与同一直线平行，那么它们也平行 ）
∴∠2＝ ∠D
又∠BED＝∠1+∠2
∴∠BED＝∠B+∠D （ 等量代换 ）．
【解答】证明：过E点作EF∥AB，
∴∠1＝∠B，
∵AB∥CD（已知），
∴EF∥CD（如果两条直线与同一直线平行，那么它们也平行），
∴∠2＝∠D，
又∵∠BED＝∠1+∠2，
∴∠BED＝∠B+∠D （等量代换）．
故答案为：∠B；如果两条直线与同一直线平行，那么它们也平行；∠D；等量代换．
13．如图，在△ABC中，CD⊥AB于D，FG⊥AB于G，ED∥BC，
求证：∠1＝∠2．
【解答】证明：∵CD⊥AB，FG⊥AB，
∴∠CDB＝∠FGB＝90°，
∴CD∥FG，
∴∠2＝∠3，
∵DE∥BC，
∴∠1＝∠3，
∴∠1＝∠2．
14．完成下面的推理填空：
如图，已知AB∥CD，∠1＝∠2，∠3＝∠4，求证：∠D＝∠DCE．
证明：∵AB∥CD，
∴∠2＝∠BAE（ 两直线平行，同位角相等 ）．
∵∠BAE＝∠3+ ∠CAE ，
∴∠2＝∠3+ ∠CAE ，
∵∠3＝∠4，
∴∠2＝∠CAD，
又∵∠2＝ ∠1 ，
∴∠CAD＝ ∠1 ，
∴AD∥ BC （ 内错角相等，两直线平行 ）．
∴∠D＝∠DCE．（ 两直线平行，内错角相等 ）．
【解答】证明：∵AB∥CD，
∴∠2＝∠BAE（两直线平行，同位角相等）．
∵∠BAE＝∠3+∠CAE，
∴∠2＝∠3+∠CAE，
∵∠3＝∠4，
∴∠2＝∠CAD，
又∵∠2＝∠1，
∴∠CAD＝∠1，
∴AD∥BC（内错角相等，两直线平行）．
∴∠D＝∠DCE（ 两直线平行，内错角相等）．
故答案为：两直线平行，同位角相等；∠CAE；∠CAE；∠1；∠1；BC；内错角相等，两直线平行；两直线平行，内错角相等．
15．完成下面的推理填空
如图，已知，F是DG上的点，∠1+∠2＝180°，∠3＝∠B，求证：∠AED＝∠C．
证明：∵F是DG上的点（已知）
∴∠2+∠DFE＝180° （ 邻补角的定义 ）
又∵∠1+∠2＝180°（已知）
∴∠1＝∠DFE （ 等角的补角相等 ）
∴BD∥EF （ 内错角相等，两直线平行 ）
∴∠3＝∠ADE （ 两直线平行，内错角相等 ）
又∵∠3＝∠B（已知）
∴∠B＝∠ADE （ 等量代换 ）
∴DE∥BC （ 同位角相等，两直线平行 ）
∴∠AED＝∠C （ 两直线平行，同位角相等 ）
【解答】解：∵F是DG上的点（已知）
∴∠2+∠DFE＝180° （邻补角的定义）
又∵∠1+∠2＝180°（已知）
∴∠1＝∠DFE （等角的补角相等）
∴BD∥EF （内错角相等，两直线平行）
∴∠3＝∠ADE （两直线平行，内错角相等）
又∵∠3＝∠B（已知）
∴∠B＝∠ADE （等量代换）
∴DE∥BC （同位角相等，两直线平行）
∴∠AED＝∠C （两直线平行，同位角相等）
故答案为：邻补角的定义；等角的补角相等；内错角相等，两直线平行；等量代换；同位角相等，两直线平行；两直线平行，同位角相等．
16．如图，点F在线段AB上，点E、G在线段CD上，AB∥CD．
（1）若BC平分∠ABD，∠D＝100°，求∠ABC的度数．
解：∵AB∥CD（已知），
∴∠ABD+∠D＝180°，（ 两直线平行，同旁内角互补 ）
∵∠D＝100°，（已知）
∴∠ABD＝ 80 °，
∵BC平分∠ABD，（已知）
∴∠ABC＝∠ABD＝40°．（角平分线的定义）
（2）若∠1＝∠2，求证：AE∥FG．
【解答】（1）解：∵AB∥CD（已知），
∴∠ABD+∠D＝180°，（两直线平行，同旁内角互补），
∵∠D＝100°，（已知）
∴∠ABD＝80°，
∵BC平分∠ABD（已知），
∴∠ABC＝∠ABD＝40°（角平分线的定义），
故答案为：两直线平行，同旁内角互补，80；
（2）证明：∵AB∥CD，
∴∠1＝∠FGC，
∵∠1＝∠2，
∴∠2＝∠FGC，
∴AE∥FG．
17．完成下面的推理填空：
已知：如图，E、F分别在AB和CD上，∠1＝∠D，∠2与∠C互余，AF⊥CE于G．
求证：AB∥CD．
证明：∵AF⊥CE
∴∠CGF＝90°
∵∠1＝∠D（已知）
∴ AF ∥ DE （ 同位角相等，两直线平行 ）
∴∠4＝∠CGF＝90° （ 两直线平行，同位角相等 ）
又∵∠2与∠C互余（已知），∠2+∠3+∠4＝180°
∴∠2+∠C＝∠2+ ∠3 ＝90°
∴∠C＝ ∠3
∴AB∥CD．
【解答】解：∵AF⊥CE，
∴∠CGF＝90°（垂直的定义）
∵∠1＝∠D（已知）
∴AF∥DE（同位角相等，两直线平行），
∴∠4＝∠CGF＝90° （两直线平行，同位角相等），
又∵∠2与∠C互余（已知），∠2+∠3+∠4＝180°，
∴∠2+∠C＝∠2+∠3＝90°，
∴∠C＝∠3，
∴AB∥CD （内错角相等，两直线平行）．
故答案为：AF，DE；同位角相等，两直线平行；两直线平行，同位角相等；∠3；∠3．
18．如图，AB交CD于O，OE⊥AB．
（1）若∠EOD＝20°，求∠AOC的度数；
（2）若∠AOC：∠BOC＝1：2，求∠EOD的度数．
【解答】解：（1）∵OE⊥AB，
∴∠AOE＝90°，
∵∠EOD＝20°，
∴∠AOC＝180°﹣90°﹣20°＝70°；
（2）设∠AOC＝x，则∠BOC＝2x，
∵∠AOC+∠BOC＝180°，
∴x+2x＝180°，
解得：x＝60°，
∴∠AOC＝60°，
∴∠BOD＝60°，
∴∠EOD＝180°﹣90°﹣60°＝30°．
19．如图，已知∠ABC＝180°﹣∠A，BD⊥CD于D，EF⊥CD于E．
（1）求证：AD∥BC；
（2）若∠ADB＝36°，求∠EFC的度数．
【解答】（1）证明：∵∠ABC＝180°﹣∠A，
∴∠ABC+∠A＝180°，
∴AD∥BC；
（2）∵AD∥BC，∠ADB＝36°，
∴∠DBC＝∠ADB＝36°，
∵BD⊥CD，EF⊥CD，
∴BD∥EF，
∴∠DBC＝∠EFC＝36°
20．阅读下列文字，并完成证明；
已知：如图，∠1＝∠4，∠2＝∠3，求证：AB∥CD；
证明：如图，延长CF交AB于点G
∵∠2＝∠3
∴BE∥CF（ 内错角相等，两直线平行 ）
∴∠1＝ ∠AGF （两直线平行，同位角相等）
又∠1＝∠4
∴∠AGF＝ ∠4 （ 等量代换 ）
∴AB∥CD（内错角相等，两直线平行）
【解答】证明：如图，延长CF交AB于点G
∵∠2＝∠3
∴BE∥CF（ 内错角相等，两直线平行）
∴∠1＝∠AGF（两直线平行，同位角相等）
又∠1＝∠4
∴∠AGF＝∠4（ 等量代换）
∴AB∥CD（内错角相等，两直线平行）．
故答案为：内错角相等，两直线平行；∠AGF；∠4；等量代换．
21．如图，点B，E分别在AC，DF上，BD，CE均与AF相交，∠A＝∠F，∠C＝∠D，求证：∠1＝∠2．
【解答】证明：∵∠A＝∠F，
∴AC∥DF，
∴∠3＝∠D；
又∵∠C＝∠D，
∴∠C＝∠3，
∴BD∥CE，
∴∠1＝∠4，
∵∠2＝∠4，
∴∠1＝∠2．
22．已知：如图EF∥CD，∠1+∠2＝180°．
（1）试说明GD∥CA；
（2）若CD平分∠ACB，DG平分∠CDB，且∠A＝40°，求∠ACB的度数．
【解答】解：（1）∵EF∥CD
∴∠1+∠ECD＝180°
又∵∠1+∠2＝180°
∴∠2＝∠ECD
∴GD∥CA
（2）由（1）得：GD∥CA，
∴∠BDG＝∠A＝40°，∠ACD＝∠2，
∵DG平分∠CDB，
∴∠2＝∠BDG＝40°，
∴∠ACD＝∠2＝40°，
∵CD平分∠ACB，
∴∠ACB＝2∠ACD＝80°．
23．如图，在三角形ABC中，点D、G分别为边BC、AB上的点，DE⊥AC于点E，BF⊥AC于点F，连接FG，且∠BFG+∠BDE＝180°．
（1）求证：DE∥BF；
（2）猜想∠AGF与∠ABC的数量关系，并证明你的猜想．
【解答】证明：（1）∵DE⊥AC于点E，BF⊥AC于点F，
∴∠CED＝∠EFB＝90°，
∴DE∥BF；
（2）∠AGF＝∠ABC，理由如下：
∵DE∥BF，
∴∠BDE+∠DBF＝180°，
∵∠BFG+∠BDE＝180°．
∴∠BFG＝∠DBF，
∴FG∥BC，
∴∠AGF＝∠ABC
24．已知：如图，AE⊥BC，FG⊥BC，∠1＝∠2
（1）求证：AB∥CD
（2）若∠D＝∠3+50°，∠CBD＝70°，求∠C的度数．
【解答】（1）证明：∵AE⊥BC，FG⊥BC，
∴∠AMB＝∠GNM＝90°，
∴AE∥FG，
∴∠A＝∠2；
又∵∠2＝∠1，
∴∠A＝∠1，
∴AB∥CD；
（2）解：∵AB∥CD，
∴∠D+∠CBD+∠3＝180°，
∵∠D＝∠3+50°，∠CBD＝70°，
∴∠3＝30°，
∵AB∥CD，
∴∠C＝∠3＝30°．
25．如图，在三角形ABC中，D，E，F分别是三边上的点，且DE平分∠ADF，∠ADF＝2∠DFB．
（1）判断DE与BC是否平行，并说明理由．
（2）若EF∥AB，∠DFE＝3∠CFE，求∠ADE的度数．
【解答】解：（1）DE∥BC，理由：
∵DE平分∠ADF，
∴∠ADF＝2∠EDF，
又∵∠ADF＝2∠DFB，
∴∠EDF＝∠DFB，
∴DE∥BC；
（2）设∠EFC＝α，则∠DFE＝3∠CFE＝3α，
∵EF∥AB，
∴∠B＝∠EFC＝α，
又∵DE∥BC，
∴∠ADE＝∠B＝α，
∵DE平分∠ADF，DE∥BC，
∴∠DFB＝∠EDF＝∠ADE＝α，
∵∠DFB+∠DFE+∠CFE＝180°，
∴α+3α+α＝180°，
解得α＝36°，
∴∠ADE＝36°．
26．如图，AB∥CD，AE平分∠BAD，CD与AE相交于F，∠CFE＝∠E．求证：AD∥BC．
【解答】证明：∵AE平分∠BAD，
∴∠1＝∠2，
∵AB∥CD，∠CFE＝∠E，
∴∠1＝∠CFE＝∠E，
∴∠2＝∠E，
∴AD∥BC．
27．完成下面的推理，并在括号内标注理由：
如图，∠DEH+∠EHG＝180°，∠1＝∠2，∠C＝∠A．
求证：∠AEH＝∠F．
证明：∵∠DEH+∠EHG＝180°，
∴ED∥ AC （ 同旁内角互补，两直线平行 ）．
∴∠1＝∠C（ 两直线平行，同位角相等 ）．
∠2＝ ∠DGC （ 两直线平行，内错角相等 ）．
∵∠1＝∠2，∠C＝∠A（ 已知 ），
∴∠A＝ ∠DGC ．
∴AB∥DF（ 同位角相等，两直线平行 ）．
∴∠AEH＝∠F（ 两直线平行，内错角相等 ）．
【解答】证明：∵∠DEH+∠EHG＝180°，
∴ED∥AC（同旁内角互补，两直线平行），
∴∠1＝∠C（两直线平行，同位角相等），
∠2＝∠DGC（两直线平行，内错角相等），
∵∠1＝∠2，∠C＝∠A（已知），
∴∠A＝∠DGC，
∴AB∥DF（同位角相等，两直线平行），
∴∠AEH＝∠F（两直线平行，内错角相等），
故答案为：AC；同旁内角互补，两直线平行；两直线平行，同位角相等；∠DGC；两直线平行，内错角相等；已知；∠DGC；同位角相等，两直线平行；两直线平行，内错角相等．
28．如图，∠BAP+∠APD＝180°，∠1＝∠2，求证：∠E＝∠F．
【解答】证明：∵∠BAP+∠APD＝180°（已知），
∴AB∥CD（同旁内角互补，两直线平行）．
∴∠BAP＝∠APC（两直线平行，内错角相等）．
又∵∠1＝∠2（已知），
∴∠FPA＝∠EAP，
∴AE∥PF（内错角相等，两直线平行）．
∴∠E＝∠F（两直线平行，内错角相等）．
29．如图，CD⊥AB于D，点F是BC上任意一点，FE⊥AB于E，且∠1＝∠2，∠3＝80°．
（1）试证明∠B＝∠ADG；
（2）求∠BCA的度数．
【解答】（1）证明：∵CD⊥AB，FE⊥AB，
∴CD∥EF，
∴∠2＝∠BCD，
∵∠1＝∠2，
∴∠1＝∠BCD，
∴BC∥DG，
∴∠B＝∠ADG；
（2）解：∵DG∥BC，
∴∠3＝∠BCG，
∵∠3＝80°，
∴∠BCA＝80°．
30．如图，EF∥AD，∠1＝∠2，∠BAC＝80°．将求∠AGD的过程填写完整．
因为EF∥AD，
所以∠2＝ ∠3 （ 两直线平行，同位角相等 ），
又因为∠1＝∠2，
所以∠1＝∠3（ 等量代换 ），
所以AB∥ DG （ 内错角相等，两直线平行 ），
所以∠BAC+ ∠AGD ＝180°（ 两直线平行，同旁内角互补 ），
因为∠BAC＝80°，
所以∠AGD＝ 100° ．
【解答】解：∵EF∥AD，
∴∠2＝∠3（两直线平行，同位角相等）；
又∵∠1＝∠2，
∴∠1＝∠3（等量代换），
∴AB∥DG（内错角相等，两直线平行），
∴∠BAC+∠AGD＝180°（两直线平行，同旁内角互补），
∵∠BAC＝80°，
∴∠AGD＝100°．
31．请补全证明过程及推理依据．
已知：如图，BC∥ED，BD平分∠ABC，EF平分∠AED．
求证：BD∥EF．
证明：∵BD平分∠ABC，EF平分∠AED，
∴∠1＝∠AED，∠2＝∠ABC（ 角平分线的定义 ）．
∵BC∥ED，
∴∠AED＝ ∠ABC （ 两直线平行，同位角相等 ）
∴∠AED＝∠ABC．
∴∠1＝∠2（ 等量代换 ）．
∴BD∥EF（ 同位角相等，两直线平行 ）．
【解答】证明：∵BD平分∠ABC，EF平分∠AED，
∴∠1＝∠AED，∠2＝∠ABC（角平分线的定义），
∵BC∥ED，
∴∠AED＝∠ABC（两直线平行，同位角相等），
∴∠AED＝∠ABC，
∴∠1＝∠2（等量代换），
∴BD∥EF（同位角相等，两直线平行），
故答案为：角平分线的定义，∠ABC，两直线平行，同位角相等，等量代换，同位角相等，两直线平行．
32．已知：如图，点D、E、G分别是△ABC边BC、AB和AC上的点，AD∥EF，点F在BC上，∠1＝∠2＝∠B．
求证：①AB∥DG；
②DG平分∠ADC．
【解答】证明：①∵EF∥AD，
∴∠1＝∠BAD，
∵∠1＝∠2，
∴∠2＝∠BAD，
∴AB∥DG；
②∵AB∥DG，
∴∠B＝∠CDG，
∵∠2＝∠B，
∴∠2＝∠CDG，
∴DG平分∠ADC．
33．如图，已知AD⊥BC，EF⊥BC，垂足分别为D、F，∠2+∠3＝180°，试说明：∠GDC＝∠B．请补充说明过程，并在括号内填上相应的理由．
解：∵AD⊥BC，EF⊥BC（已知）
∴∠ADB＝∠EFB＝90° （ 垂直的定义 ），
∴EF∥AD（ 同位角相等两直线平行 ），
∴ ∠1 +∠2＝180°（ 两直线平行同旁内角互补 ）．
又∵∠2+∠3＝180°（已知），
∴∠1＝∠3（ 同角的补角相等 ），
∴AB∥ DG （ 内错角相等两直线平行 ），
∴∠GDC＝∠B（ 两直线平行同位角相等 ）．
【解答】解：∵AD⊥BC，EF⊥BC（已知）
∴∠ADB＝∠EFB＝90°（垂直的定义），
∴EF∥AD （同位角相等两直线平行），
∴∠1+∠2＝180°（两直线平行同旁内角互补），
又∵∠2+∠3＝180°（已知），
∴∠1＝∠3 （同角的补角相等），
∴AB∥DG（内错角相等两直线平行），
∴∠GDC＝∠B （两直线平行同位角相等）．
故答案为：垂直的定义，同位角相等两直线平行，∠1，两直线平行同旁内角互补，同角的补角相等，DG，内错角相等两直线平行，两直线平行同位角相等．
34．如图，BD平分∠ABC，F在AB上，G在AC上，FC与BD相交于点H，∠3+∠4＝180°，试说明∠1＝∠2．（请通过填空完善下列推理过程）
解：∵∠3+∠4＝180°（已知），∠FHD＝∠4（ 对顶角相等 ）．
∴∠3+ ∠FHD ＝180°（等量代换）．
∴FG∥BD（ 同旁内角互补，两直线平行 ）．
∴∠1＝ ∠ABD （ 两直线平行，同位角相等 ）．
∵BD平分∠ABC，
∴∠ABD＝ ∠2 （ 角平分线的定义 ）．
∴∠1＝∠2（ 等量代换 ）．
【解答】解：∵∠3+∠4＝180°（已知），∠FHD＝∠4（对顶角相等），
∴∠3+∠FHD＝180°（等量代换），
∴FG∥BD（同旁内角互补，两直线平行），
∴∠1＝∠ABD（两直线平行，同位角相等），
∵BD平分∠ABC，
∴∠ABD＝∠2（角平分线的定义），
∴∠1＝∠2（等量代换），
故答案为：对顶角相等，∠FHD，同旁内角互补，两直线平行，∠ABD，两直线平行，同位角相等，∠2，角平分线的定义，等量代换．
35．如图，D，E分别在△ABC的边AB，AC上，F在线段CD上，且∠1+∠2＝180°，DE∥BC．
（1）求证：∠3＝∠B；
（2）若DE平分∠ADC，∠2＝3∠B，求∠1的度数．
【解答】解：（1）∵∠1+∠DFE＝180°，∠1+∠2＝180°，
∴∠2＝∠DFE，
∴AB∥EF，
∴∠3＝∠ADE，
∵DE∥BC，
∴∠ADE＝∠B，
∴∠3＝∠B．
（2）∵DE平分∠ADC，
∴∠ADE＝∠EDC，
∵DE∥BC，
∴∠ADE＝∠EDC＝∠B，
∵∠2＝3∠B，∠2+∠ADE+∠EDC＝180°，
∴5∠B＝180°，
∴∠B＝36°，
又∵∠3＝∠B，
∴∠1＝∠3+∠EDC＝36°+36°＝72°．
36．请根据条件进行推理，得出结论，并在括号内注明理由．
已知：如图，BD⊥AC，EF⊥AC，∠1+∠2＝180°．
求证：DG∥BC．
证明：∵BD⊥AC，EF⊥AC（已知），
∴∠BDC＝∠EFC＝90°（垂直的定义）．
∴ BD ∥ EF （ 同位角相等，两直线平行 ）．
∴∠2+ ∠DBE ＝180°（ 两直线平行，同旁内角互补 ）．
又∵∠1+∠2＝180°（已知），
∴∠1＝ ∠DBE （ 等量代换 ）．
∴DG∥BC（ 内错角相等，两直线平行 ）．
【解答】证明：∵BD⊥AC，EF⊥AC（已知），
∴∠BDC＝∠EFC＝90°（垂直的定义）．
∴BD∥EF（同位角相等，两直线平行）．
∴∠2+∠DBE＝180°（两直线平行，同旁内角互补）．
又∵∠1+∠2＝180°（已知），
∴∠1＝∠DBE（等量代换）．
∴DG∥BC（内错角相等，两直线平行）．
故答案为：BD∥EF；同位角相等，两直线平行；∠DBE；两直线平行，同旁内角互补；∠DBE；等量代换；内错角相等，两直线平行．
37．如图，已知AB∥CD，∠1＝∠2，求证：BE∥GF．
【解答】证明：∵AB∥CD，
∴∠1＝∠BED，
∵∠1＝∠2，
∴∠BED＝∠2，
∴BE∥GF．
38．完成下列推理说明：
（1）如图1，已知∠1＝∠2，∠B＝∠C，可推出AB∥CD．理由如下：
因为∠1＝∠2（已知），且∠1＝∠4（ 对顶角相等 ）
所以∠2＝∠4（等量代换）
所以CE∥BF（ 同位角相等，两直线平行 ）
所以∠ C ＝∠3（ 两直线平行，同位角相等 ）
又因为∠B＝∠C（已知）
所以∠3＝∠B（等量代换）
所以AB∥CD（ 内错角相等，两直线平行 ）
（2）如图2，已知∠B+∠BCD＝180°，∠B＝∠D．求证：∠E＝∠DFE．
证明：∵∠B+∠BCD＝180°（ 已知 ），
∴AB∥CD （ 同旁内角互补，两直线平行 ）
∴∠B＝ ∠DCE （ 两直线平行，同位角相等 ）
又∵∠B＝∠D（ 已知 ），
∴∠ DCE ＝∠ D （等量代换）
∴AD∥BE（ 内错角相等，两直线平行 ）
∴∠E＝∠DFE（ 两直线平行，内错角相等 ）
【解答】解：（1）理由：
因为∠1＝∠2（已知），且∠1＝∠4（对顶角相等），
所以∠2＝∠4（等量代换），
所以CE∥BF（同位角相等，两直线平行），
所以∠C＝∠3（两直线平行，同位角相等），
又因为∠B＝∠C（已知），
所以∠3＝∠B（等量代换），
所以AB∥CD（内错角相等，两直线平行）；
故答案为：对顶角相等，同位角相等，两直线平行，C，两直线平行，同位角相等，内错角相等，两直线平行；
（2）证明：∵∠B+∠BCD＝180°（已知），
∴AB∥CD （同旁内角互补，两直线平行），
∴∠B＝∠DCE（两直线平行，同位角相等），
又∵∠B＝∠D（已知），
∴∠DCE＝∠D （等量代换），
∴AD∥BE（内错角相等，两直线平行），
∴∠E＝∠DFE（两直线平行，内错角相等）．
故答案为：同旁内角互补，两直线平行，∠DCE，两直线平行，同位角相等，DCE，D，内错角相等，两直线平行，两直线平行，内错角相等．
39．如图，已知AB∥CD，∠1＝∠2，CF平分∠DCE．
（1）试判断直线AE与BF有怎样的位置关系？并说明理由；
（2）若∠1＝80°，求∠3的度数．
【解答】解：（1）AC∥BD．理由如下：
∵AB∥CD，
∴∠2＝∠CDF，
∵∠1＝∠2，
∴∠1＝∠CDF，
∴AE∥BF；
（2）∵∠1＝80°，
∴∠ECD＝180°﹣∠1＝180°﹣80°＝100°，
∵CF平分∠ECD，
∴∠ECF＝∠ECD＝50°．
∵AC∥BD，
∴∠3＝∠ECF＝50°．
40．阅读下列推理过程，在括号中填写理由．
已知：如图，点D、E分别在线段AB、BC上，AC∥DE，DF∥AE交BC于点F，AE平分∠BAC．求证：DF平分∠BDE
证明：∵AE平分∠BAC（已知）
∴∠1＝∠2（ 角平分线的定义 ）
∵AC∥DE（已知）
∴∠1＝∠3（ 两直线平行，内错角相等 ）
故∠2＝∠3（ 等量代换 ）
∵DF∥AE（已知）
∴∠2＝∠5，（ 两直线平行，同位角相等 ）
∠3＝∠4（ 两直线平行，内错角相等 ）
∴∠4＝∠5（ 等量代换 ）
∴DF平分∠BDE（ 角平分线的定义 ）
【解答】证明：∵AE平分∠BAC（已知）
∴∠1＝∠2（角平分线的定义）
∵AC∥DE（已知）
∴∠1＝∠3（两直线平行，内错角相等）
故∠2＝∠3（等量代换）
∵DF∥AE（已知）
∴∠2＝∠5，（两直线平行，同位角相等）
∠3＝∠4（两直线平行，内错角相等）
∴∠4＝∠5（等量代换）
∴DF平分∠BDE（角平分线的定义）．
故答案为：角平分线的定义，两直线平行，内错角相等，等量代换，两直线平行，同位角相等，等量代换，角平分线的定义．
41．如图，点D、F在线段AB上，点E、G分别在线段BC和AC上，CD∥EF，∠1＝∠2．
（1）判断DG与BC的位置关系，并说明理由；
（2）若DG是∠ADC的平分线，∠3＝85°，且∠DCE：∠DCG＝9：10，试说明AB与CD有怎样的位置关系？
【解答】解：（1）DG∥BC．
理由：∵CD∥EF，
∴∠2＝∠BCD．
∵∠1＝∠2，
∴∠1＝∠BCD，
∴DG∥BC；
（2）CD⊥AB．
理由：∵由（1）知DG∥BC，∠3＝85°，
∴∠BCG＝180°﹣85°＝95°．
∵∠DCE：∠DCG＝9：10，
∴∠DCE＝95°×＝45°．
∵DG是∠ADC的平分线，
∴∠ADC＝2∠CDG＝90°，
∴CD⊥AB．
42．如图，点D、E、F、G均在△ABC的边上，连接BD、DE、FG，∠3＝∠CBA，FG∥BD．
（1）求证：∠1+∠2＝180°；
（2）若BD平分∠CBA，DE平分∠BDC，∠A＝35°，求∠C的度数．
【解答】（1）证明：∵∠3＝∠CBA，
∴AB∥DE，
∴∠2＝∠DBA，
∵FG∥BD，
∴∠1+∠DBA＝180°，
∴∠1+∠2＝180°；
（2）解：∵AB∥DE，
∴∠CDE＝∠A＝35°，
∵DE平分∠BDC，
∴∠2＝∠CDE＝35°，
∴∠DBA＝35°，
∵BD平分∠CBA，
∴∠CBA＝70°，
∴∠C＝180°﹣∠A﹣∠CBA＝75°．
43．已知：如图，∠B＝∠ADE，∠EDC＝∠GFB，GF⊥AB．
求证：CD⊥AB．
【解答】证明：∵∠B＝∠ADE，
∴DE∥BC，
∴∠EDC＝∠DCF，
∵∠EDC＝∠GFB，
∴∠DCF＝∠GFB，
∴CD∥GF，
∴∠CDG＝∠FGB，
∵GF⊥AB
∴∠CDG＝∠FGB＝90°，
∴CD⊥AB．
44．已知：如图，AD⊥BC于D，EG⊥BC于G，∠E＝∠AFE．
求证：AD平分∠BAC．
【解答】证明：∵AD⊥BC，EG⊥BC，
∴∠ADC＝∠EGC＝90°，
∴AD∥EG（同位角相等，两直线平行），
∴∠E＝∠CAD（两直线平行，同位角相等），
∠AFE＝∠BAD（两直线平行，内错角相等），
又∵∠E＝∠AFE，
∴∠BAD＝∠CAD，
∴AD平分∠BAC．
45．请根据条件进行推理，得出结论，并在括号内注明理由．
已知：如图，∠1＝∠2，∠B+∠CDE＝180°．
求证：AB∥CD．
证明：∵∠1＝ ∠BFD （ 对顶角相等 ），
又∵∠1＝∠2，
∴∠BFD＝∠2 （ 等量代换 ）．
∴BC∥ DE （ 同位角相等，两直线平行 ）．
∴∠C+ ∠CDE ＝180° （ 两直线平行，同旁内角互补 ）．
又∵∠B+∠CDE＝180°，
∴∠B＝∠C．
∴AB∥CD （ 内错角相等，两直线平行 ）．
【解答】证明：∵∠1＝∠BFD（对顶角相等），
又∵∠1＝∠2，
∴∠BFD＝∠2（等量代换）．
∴BC∥DE（同位角相等，两直线平行）．
∴∠C+∠CDE＝180°（两直线平行，同旁内角互补）．
又∵∠B+∠CDE＝180°，
∴∠B＝∠C．
∴AB∥CD（内错角相等，两直线平行）．
故答案为：∠BFD；对顶角相等；等量代换；DE；同位角相等，两直线平行；∠CDE；两直线平行，同旁内角互补；内错角相等，两直线平行．
46．已知，如图，∠ABC＝∠ADC，BF、DE分别平分∠ABC与∠ADC，且∠1＝∠3．求证：AB∥DC．
请根据条件进行推理，得出结论，并在括号内注明理由．
证明：∵BF、DE分别平分∠ABC与∠ADC，
∴∠1＝∠ABC，∠2＝．（ 角平分线定义 ）
∵∠ABC＝∠ADC，
∵∠ 1 ＝∠ 2 ．
∵∠1＝∠3，
∴∠2＝ 3 ．（等量代换）
∴ AB ∥ CD ．（ 内错角相等，两直线平行 ）
【解答】解∵BF、DE分别平分∠ABC与∠ADC，
∴∠1＝∠ABC，∠2＝．（角平分线定义 ）
∵∠ABC＝∠ADC，
∵∠1＝∠2．
∵∠1＝∠3，
∴∠2＝∠3．（等量代换）
∴AB∥CD．（内错角相等，两直线平行）
故答案为：角平分线定义；1；2；∠3；AB；CD；内错角相等，两直线平行．
47．如图AB∥CD，点P是平面内直线AB、CD外一点连接PA、PC．
（1）写出所给的四个图形中∠APC、∠PAB、∠PCD之间的数量关系；
（2）证明图（1）和图（3）的结论．
【解答】解：（1）如图1，∠APC+∠PAB+∠PCD＝360°，
如图2，∠APC＝∠PAB+∠PCD，
如图3，∠APC＝∠PCD﹣∠PAB，
如图4，∠APC＝∠PAB﹣∠PCD．
（2）如图1，过P作PE∥AB，
∵AB∥CD，
∴PE∥CD，
∴∠A+∠APE＝180°，∠C+∠CPE＝180°，
∴∠A+∠APE+∠C+∠CPE＝360°，即∠APC+∠PAB+∠PCD＝360°；
如图3，过P作PE∥AB，
∵AB∥CD，
∴PE∥CD，
∴∠PCD＝∠CPE，∠PAB＝∠APE，
∴∠APC＝∠CPE﹣∠APE＝∠C﹣∠A．
48．如图，直线AB，CD相交于点O，OE平分∠BOC，OF⊥CD．
（1）若∠AOF＝50°，求∠BOE的度数；
（2）若∠BOD：∠BOE＝1：4，求∠AOF的度数．
【解答】解：（1）∵∠COF与∠DOF是邻补角，
∴∠COF＝180°﹣∠DOF＝90°．
∵∠AOC与∠AOF互为余角，
∴∠AOC＝90°﹣∠AOF＝90°﹣50°＝40°．
∵∠AOC与∠BOC是邻补角，
∴∠COB＝180°﹣∠AOC＝180°﹣40°＝140°．
∵OE平分∠BOC，
∴∠BOE＝∠BOC＝70°；
解法二：∵OF⊥CD，
∴∠COF＝90°，
∵∠AOF＝50°，
∴∠AOC＝40°，
∴∠BOC＝140°，
∵OE平分∠BOC，
∴∠BOE＝∠BOC＝70°．
（2）∠BOD：∠BOE＝1：4，
设∠BOD＝∠AOC＝x，∠BOE＝∠COE＝4x．
∵∠AOC与∠BOC是邻补角，
∴∠AOC+∠BOC＝180°，
即x+4x+4x＝180°，
解得x＝20°．
∵∠AOC与∠AOF互为余角，
∴∠AOF＝90°﹣∠AOC＝90°﹣20°＝70°．
49．如图，已知∠1＝∠2＝52°，EF∥DB．
（1）DG与AB平行吗？请说明理由；
（2）若EC平分∠FED，求∠C的度数．
【解答】解：（1）DG与AB平行．理由：
∵EF∥DB，
∴∠1＝∠D．
∵∠1＝∠2，
∴∠D＝∠2．
∴DG∥AB．
（2）∵EC平分∠FED，
∴∠DEC＝∠DEF．
∵∠1＝52°，
∴∠DEF＝180°﹣∠1＝128°．
∴∠DEC＝∠DEF＝64°．
∵DG∥AB，
∴∠C＝∠DEC＝64°．
50．如图，已知DG∥BA，∠1＝∠2，求证：AD∥EF．
【解答】证明：∵DG∥AB，
∴∠GDA＝∠BAD，
∵∠GDA＝∠BEF，
∴∠BAD＝∠BEF，
即∠2＝∠3，
∴EF∥AD．
51．如图，已知AD∥CB，∠A＝∠C，若∠ABD＝32°，求∠BDC的度数．有同学用了下面的方法．但由于一时犯急没有写完整，请你帮他添写完整．
解：∵AD∥CB（ 已知 ）
∴∠C+∠ADC＝180° （ 两直线平行，同旁内角互补 ）
又∵∠A＝∠C （ 已知 ）
∴∠A+∠ADC＝180° （ 等量代换 ）
∴AB∥CD （ 同旁内角互补，两直线平行 ）
∴∠BDC＝∠ABD＝32° （ 两直线平行，内错角相等 ）．
【解答】解：∵AD∥CB（ 已知 ），
∴∠C+∠ADC＝180° （两直线平行，同旁内角互补）．
又∵∠A＝∠C （已知），
∴∠A+∠ADC＝180° （等量代换），
∴AB∥CD （同旁内角互补，两直线平行），
∴∠BDC＝∠ABD＝32° （两直线平行，内错角相等）．
故答案为：两直线平行，同旁内角互补；已知；等量代换；同旁内角互补，两直线平行；两直线平行，内错角相等．
52．填空，将理由补充完整
已知：如图，AB∥CD，∠B＝∠D，直线EF与AD，BC的延长线分别交于点E，F，
求证：∠DEF＝∠F．
证明：∵AB∥CD（已知），
∴∠B＝ ∠DCF （ 两直线平行，同位角相等 ），
∵∠B＝∠D（ 已知 ），
∴∠D＝ ∠DCF （ 等量代换 ），
∴AD∥ BF （ 内错角相等，两直线平行 ），
∴∠DEF＝∠F（ 两直线平行，内错角相等 ）．
【解答】证明：∵AB∥CD（已知），
∴∠B＝∠DCF（两直线平行，同位角相等），
∵∠B＝∠D（已知），
∴∠D＝∠DCF（等量代换），
∴AD∥BF（内错角相等，两直线平行），
∴∠DEF＝∠F（两直线平行，内错角相等），
故答案为：∠DCF；两直线平行，同位角相等；已知；∠DCF；等量代换；BF；内错角相等，两直线平行；两直线平行，内错角相等．
53．如图，∠AGF＝∠ABC，∠1+∠2＝180°．
（1）求证：BF∥DE；
（2）若DE⊥AC，∠2＝144°，求∠AFG的度数．
【解答】（1）证明：∵∠AGF＝∠ABC，
∴BC∥GF，
∴∠AFG＝∠C．
∵∠1+∠2＝180°，∠CDE+∠2＝180°，
∴∠1＝∠CDE．
∵∠CED＝180°﹣∠C﹣∠CDE，∠CFB＝180°﹣∠AFG﹣∠1，
∴∠CED＝∠CFB，
∴BF∥DE．
（2）解：∵DE⊥AC，BF∥DE，
∴∠AFB＝∠AED＝90°，
∵∠1+∠2＝180°，∠2＝144°，
∴∠1＝36°．
∵∠AFG+∠1＝∠AFB＝90°，
∴∠AFG＝54°．
54．已知AD⊥BC于D，FG⊥BC垂足分别为D，G，且∠1＝∠2，∠C＝50°，求∠EDC的度数．
证明：∵AD⊥BC，FG⊥BC，
∴∠ADC＝ 90° ，∠FGC＝90°（ 垂直的定义 ）．
∴ AD ∥FG（ 同位角相等，两直线平行 ）．
∴∠1＝∠3
又∵∠1＝∠2，
∴∠2＝∠3（ 等量代换 ）．
∴DE∥ AC ．
∴∠EDC+∠C＝180°（ 两直线平行，同旁内角互补 ）．
∵∠C＝50°．
∴∠EDC＝ 130 °．
【解答】证明：∵AD⊥BC，FG⊥BC，
∴∠ADC＝90°，∠FGC＝90°（垂直的定义），
∴AD∥FG（同位角相等，两直线平行），
∴∠1＝∠3．
又∵∠1＝∠2，
∴∠2＝∠3（等量代换），
∴DE∥AC．
∴∠EDC+∠C＝180°（两直线平行，同旁内角互补）．
∵∠C＝50°．
∴∠EDC＝130°．
故答案为：90°，垂直的定义；AD，同位角相等，两直线平行；等量代换；AC；两直线平行，同旁内角互补；130．
55．如图，∠1+∠2＝180°，∠3＝100°，OK平分∠DOH，求∠KOH的度数．
证明：∵∠1+∠2＝180°，
∴AB∥CD（ 同旁内角互补，两直线平行 ）．
∴∠3＝∠4（ 两直线平行，同位角相等 ）．
∵∠3＝100°，
∴∠4＝100°．
∴∠DOH＝180°﹣∠4＝80°．
∵OK平分∠DOH，
∴∠KOH＝∠DOH＝ 40° （ 角平分线定义 ）．
【解答】证明：∵∠1+∠2＝180°，
∴AB∥CD（同旁内角互补，两直线平行）．
∴∠3＝∠4（两直线平行，同位角相等）．
∵∠3＝100°，
∴∠4＝100°．
∴∠DOH＝180°﹣∠4＝80°．
∵OK平分∠DOH，
∴∠KOH＝∠DOH＝40°（角平分线定义）．
故答案为：同旁内角互补，两直线平行；两直线平行，同位角相等；40°；角平分线定义．
56．如图，∠1+∠2＝180°，∠DEF＝∠A，∠BED＝70°．
（1）求证：EF∥AB；
（2）求∠ACB的度数．
【解答】（1）证明：∵∠1+∠DFE＝180°，∠1+∠2＝180°
∴∠DFE＝∠2，
∴EF∥AB；
（2）解：∵EF∥AB，
∴∠DEF＝∠BDE，
又∵∠DEF＝∠A，
∴∠BDE＝∠A，
∴DE∥AC，
∴∠ACB＝∠DEB，
又∵∠DEB＝70°，
∴∠ACB＝70°．
57．如图，AB∥CD，直线EF分别交直线AB、CD于点M、N，MG平分∠EMB，NH平分∠CNF，求证：MG∥NH．
【解答】证明：∵MG平分∠EMB，MH平分∠CNF，
∴∠CNH＝∠CNF，∠BMG＝∠BME＝∠AMN，
∵AB∥CD，
∴∠CNF＝∠AMN，
∴∠CNF＝∠BMG，
∵AB∥CD，
∴∠CNM＝∠BMN，
∴∠CNF+∠CNM＝∠BMG+∠BMN，
即∠HNM＝∠GMN，
∴MG∥NH．
58．已知：如图，∠DAB＝∠DCB，AF平分∠DAB，CE平分∠DCB，∠FCE＝∠CEB．试说明：AF∥CE．
解：因为∠DAB＝∠DCB（ 已知 ），
又因为AF平分∠DAB，
所以 ∠FAE ＝∠DAB（ 角平分线的性质 ）．
又因为CE平分∠DCB，
所以∠FCE＝ ∠DCB （ 角平分线的性质 ）．
所以∠FAE＝∠FCE．
因为∠FCE＝∠CEB，
所以 ∠FAE ＝ ∠CEB ．
所以AF∥CE（ 同位角相等，两直线平行 ）．
【解答】解：因为∠DAB＝∠DCB（已知），
又因为AF平分∠DAB，
所以∠FAE＝∠DAB（角平分线的定义）．
又因为CE平分∠DCB，
所以∠FCE＝∠DCB（角平分线的定义）．
所以∠FAE＝∠FCE．
因为∠FCE＝∠CEB，
所以∠FAE＝∠CEB，
所以AF∥CE（同位角相等，两直线平行）．
故答案为：已知；∠FAE，角平分线的定义；∠DCB，角平分线的定义；∠FAE，∠CEB；同位角相等，两直线平行．
59．完成下列证明：如图，已知AD⊥BC，EF⊥BC，∠1＝∠2．
求证：∠BAC+∠AGD＝180°．
证明：∵AD⊥BC，EF⊥BC（已知），
∴∠EFB＝90°，∠ADB＝90°（ 垂直定义 ），
∴∠EFB＝∠ADB（等量代换），
∴EF∥AD（ 同位角相等，两直线平行 ），
∴∠1＝∠BAD（ 两直线平行，同位角相等 ），
又∵∠1＝∠2（已知），
∴∠ 2 ＝∠ BAD （等量代换），
∴DG∥BA（ 内错角相等，两直线平行 ），
∴∠BAC+∠AGD＝180°（ 两直线平行，同旁内角互补 ）．
【解答】解：∵AD⊥BC，EF⊥BC（已知），
∴∠EFB＝90°，∠ADB＝90°（垂直定义），
∴∠EFB＝∠ADB（等量代换），
∴EF∥AD（同位角相等，两直线平行），
∴∠1＝∠BAD（两直线平行，同位角相等），
又∵∠1＝∠2（已知），
∴∠2＝∠BAD（等量代换），
∴DG∥BA（内错角相等，两直线平行），
∴∠BAC+∠AGD＝180°（两直线平行，同旁内角互补）．
故答案为：垂直定义；同位角相等，两直线平行；两直线平行，同位角相等；2；BAD；内错角相等，两直线平行；两直线平行，同旁内角互补．
60．如图，已知∠1＝∠BDC，∠2+∠3＝180°．
（1）请你判断DA与CE的位置关系，并说明理由；
（2）若DA平分∠BDC，CE⊥AE于E，∠1＝70°，试求∠FAB的度数．
【解答】解：（1）AD∥EC，
理由是：∵∠1＝∠BDC，
∴AB∥CD，
∴∠2＝∠ADC，
又∵∠2+∠3＝180°，
∴∠ADC+∠3＝180°，
∴AD∥EC．
（2）∵DA平分∠BDC，
∴∠ADC＝∠BDC＝35°，
∴∠2＝∠ADC＝35°，
∵CE⊥AE，AD∥EC，
∴∠FAD＝∠AEC＝90°，
∴∠FAB＝∠FAD﹣∠2＝90°﹣35°＝55°．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2024/3/5 15:17:51；用户：15124787749；邮箱：15124787749；学号：20750791