湖北省襄阳市第四中学2024-2025学年八上9月数学试题（word版含答案）

这是一份湖北省襄阳市第四中学2024-2025学年八上9月数学试题（word版含答案），共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题：（每小题3分，共36分）．在每小题给出的选项中，只有一项是符合题目要求的．
1. 如图所示，为估计池塘岸边A、B的距离，小方在池塘的一侧选取一点O，测得米，米，A、B间的距离不可能是（ ）
A. 5米B. 15米C. 10米D. 20米
2. 不是利用三角形稳定性是（ ）
A. 自行车的三角形车架B. 三角形房架
C. 照相机的三脚架D. 学校的栅栏门
3. 如图，在中，边上的高为（ ）
A. B. C. D.
4. 在下列条件中：①，②，③，④，⑤中，能确定是直角三角形的条件有（ ）
A. 2个B. 3个C. 4个D. 5个
5. 如图，在△ABC中，∠A=60度，点D，E分别在AB，AC上，则∠1+∠2的大小为（ ）度.
A. 140B. 190C. 320D. 240
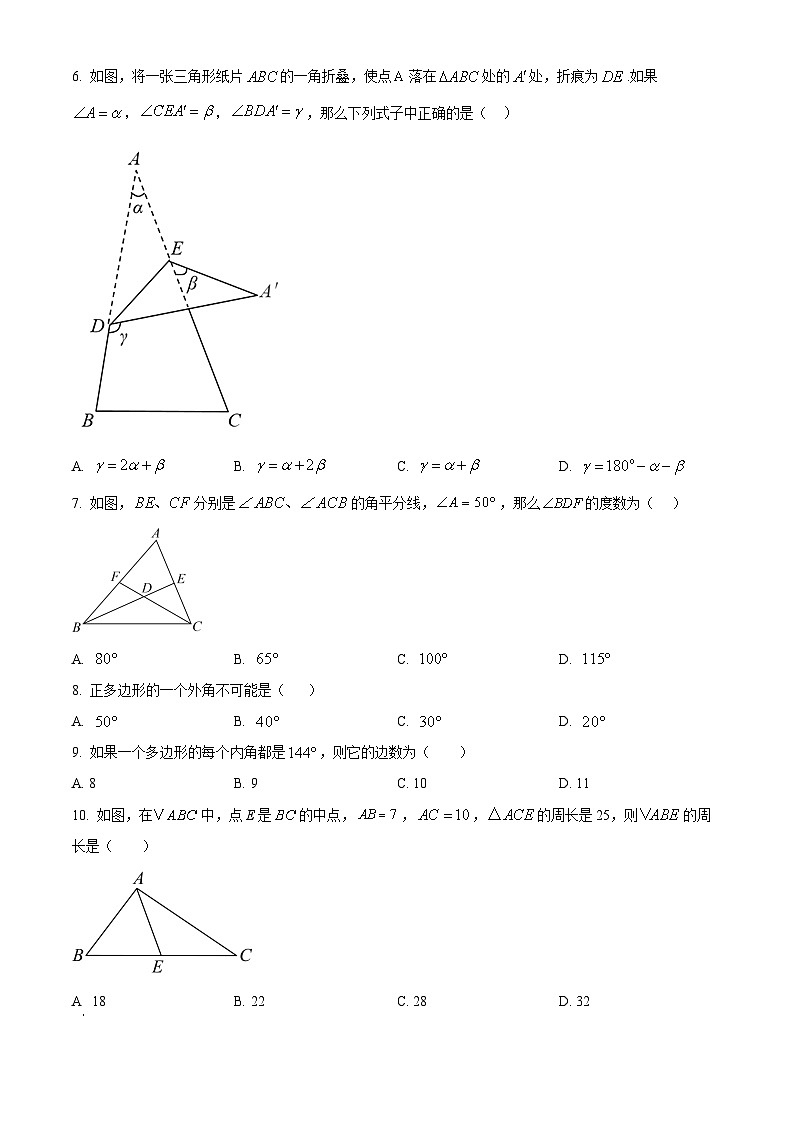
6. 如图，将一张三角形纸片的一角折叠，使点落在处的处，折痕为.如果，，，那么下列式子中正确的是（ ）
A. B. C. D.
7. 如图，分别是的角平分线，，那么的度数为（ ）
A. B. C. D.
8. 正多边形的一个外角不可能是（ ）
A. B. C. D.
9. 如果一个多边形的每个内角都是，则它的边数为（ ）
A. 8B. 9C. 10D. 11
10. 如图，在中，点E是的中点，，，的周长是25，则的周长是（ ）

A 18B. 22C. 28D. 32
11. 如图，△ACE≌△DBF，AD=8，BC=2，则 AC=（ ）
A. 2B. 8C. 5D. 3
12. 如图，已知，再添加一个条件，仍不能判定的是（ ）
A B. C. D.
二、填空题：本题共6小题，每小题3分，共18分．
13. 如图，已知AB∥CF，E为AC的中点，若FC＝6cm，DB＝3cm，则AB＝________．

14. 如图，小明从A点出发，前进6m到点B处后向右转，再前进6m到点C处后又向右转，…，这样一直走下去，他第一次回到出发点A时，一共走了 _____m．
15. 已知一个边形内角和等于1980°，则__________．
16. 如图，△ABC的面积为18，BD=2DC，AE=EC，那么阴影部分的面积是_______．
17. 如图，是的外角，平分平分，且交于点D．若，则的度数为___________．
18. △ABC中，AD是BC边上的高，∠BAD=50°，∠CAD=20°，则∠BAC=___________．
三、解答题：本题共7小题，共66分．解答应写出文字说明，证明过程或演算步骤．
19. 如图，在中，，是边上的高．求的度数．
20. 如图，点上，点在上，，，求证：．
21. 如图，，，，，求的度数与的长．
22. 如图，，，点B在上，点D在上．
求证：
（1）
（2）．
23. （1）阅读理解：课外兴趣小组活动时，老师提出了如下问题：
在中，，，求边上的中线的的取值范围．
小明在组内经过合作交流，得到了如下的解决方法（如图1）：
①延长到Q，使得；
②再连接，把集中在中；
根据小明的方法，请直接写出图1中的取值范围是 ．
（2）写出图1中与的位置关系并证明．
（3）如图2，在中，为中线，E为上一点，、交于点F，且．求证：．

24. 如图（1），，，，垂足分别为A、B，点P在线段上以的速度由点A向点B运动，同时点Q在射线BD上运动．它们运动的时间为（当点P运动结束时，点Q运动随之结束）．
（1）若点Q的运动速度与点P的运动速度相等，当时，与是否全等，并判断此时线段和线段的位置关系，请分别说明理由；
（2）如图（2），若“，”改为“”，点Q的运动速度为，其它条件不变，当点P、Q运动到何处时有与全等，求出相应的x和t的值．
25. 如图，在四边形ABCD中，AD＝AB，DC＝BC，∠DAB＝60°，∠DCB＝120°，E是AD上一点，F是AB延长线上一点，且DE＝BF．
（1）求证：CE＝CF；
（2）若G在AB上且∠ECG＝60°，试猜想DE，EG，BG之间的数量关系，并证明．
1.A
2. D
3.C
4. C【解析】解：①∵，则，，
∴是直角三角形；
②∵，设，
则，，，
∴是直角三角形；
③∵，
∴，
则，
∴是直角三角形；
④∵，
∴，
则，
∴是直角三角形；
⑤∵，，，
∴为钝角三角形．
∴能确定是直角三角形的有①②③④共4个，
故选C．
5. D【解析】分析：根据三角形外角性质可得∠1=∠A+∠ADE，∠2=∠A+∠AED，再根据已知和三角形内角和等于180°即可求解.
详解：∵∠1=∠A+∠ADE，∠2=∠A+∠AED
∴∠1+∠2
=∠A+∠ADE+∠A+∠AED
=∠A+(∠ADE+∠A+∠AED)
=60°+180°
=240°
故选D.
6. A
【解析】
由折叠得：∠A=∠A'，
∵∠BDA'=∠A+∠AFD，∠AFD=∠A'+∠CEA'，
∵∠A=α，∠CEA′=β，∠BDA'=γ，
∴∠BDA'=γ=α+α+β=2α+β，
故选A.
7. B
【解析】解：∵，
∴，
∵分别是的角平分线，
∴，
∴，
∴．
故选：B
8. A
【解析】解：A、不是整数，正多边形的一个外角不能是，符合题意；
B、，正十边形的一个外角可能是，不符合题意；
C、，正八边形的一个外角可能是，不符合题意；
D、，正十八边形的一个外角可能是，不符合题意．
故选：A．
9. C
【解析】解：∵一个多边形的每个内角都是，
∴这个多边形的每个外角都为，
∴它的边数为，
故选：C．
10. B【解析】∵点E是的中点，
∴，
∵，，
∴的周长，
∴，
∴的周长，
故选：B．
11. 如图，△ACE≌△DBF，AD=8，BC=2，则 AC=（ ）
A. 2B. 8C. 5D. 3
【答案】C
【解析】解：∵△ACE≌△DBF，
∴AC=DB，
∴AB+BC=DC+BC，即AB=DC，
∵AD=8，BC=2，
∴AB+BC+DC=8，
∴2AB+2=8，
∴AB=3，
∴AC=AB+BC=5，
故选C．
12. A
【解析】
解：A. 当添加时，且，，由“”不能证得，故选项符合题意；
B. 当添加时，且，，由“”能证得，故选项不符合题意；
C 当添加时，且，，由“”能证得，故选项不符合题意；
D. 当添加时，且，，由“”能证得，故选项不符合题意；
故选：．
二、填空题：本题共6小题，每小题3分，共18分．
13. 9cm
【解析】AB∥CF，
E为AC的中点，
△ADE≌△CFE,
故答案为
14.
【解析】解：由题意可知，当她第一次回到出发点A时，所走过的图形是一个正多边形，
由于正多边形的外角和是，且每一个外角为，
，
所以它是一个正十八边形，
因此所走的路程为（m），
故答案为：．
15. 13
【解析】解：依题意有：
（n-2）•180°=1980°，
解得n=13．
故答案为：13．
16.
【解析】如图：
作DG∥AC，交BE于点G，设阴影部分的面积a，
∵DG∥AC，BD=2DC，
∴GD=EC,BD=BC，
∴△BGD的面积=△BCE的面积，
∵△ABC的面积为18，AE=EC，
∴△BCE的面积=△ABC的面积=9，
∴△BGD的面积=△BCE的面积=4，
又∵△GDF∽△EAF,且=，
∴△GDF的面积=△EAF的面积，
∵BD=2DC，
∴△ADC的面积=18×=6，
∴△EAF的面积=6−a，
∴△GDF的面积=△EAF的面积=(6−a)，
∴△BGD的面积+△GDF的面积+阴影部分的面积a=9，
∴4+ (6−a)+a=9,解得a=.
故答案为.
17.
【解析】解：∵平分平分，
∴．
∴．
∵，
∴．
故答案为：．
70°或30°
①如图，当AD在△ABC的内部时，
∠BAC=∠BAD+∠CAD=50°+20°=70°．
②如图，当AD在△ABC的外部时，
∠BAC=∠BAD -∠CAD=50°-20°=30°．
故答案为：70°或30°．
三、解答题：本题共7小题，共66分．解答应写出文字说明，证明过程或演算步骤．
19. 解：∵，
∴，
∴．则．
又是边上的高，
．
20. ∵，，
∴，即，
在和中，
∵
∴（SAS），
∴.
21. 解：∵，
∴，．
∴
∵，
∴，
∴．
∴．
22.（1）证明：在和中，
∴
（2）∵，
∴．
∵，，
∴．
23. 解：（1）延长到Q，使得，再连接，

∵是的中线，
∴，
又∵，，
∴，
∴，
在中，，
∴，即，
∴，
故答案为：；
（2），证明如下：
由（1）知，
∴，
∴；
（3）延长至点G，使，连接，

∵为边上的中线，
∴，
在和中，
，
∴，
∴，
∵，
∴，
∴，
∴，
∴，
∴．
24. （1）解：，．
理由：∵，，
∴，
∵，
∴，
∴，
在和中，，
∴，
∴，
∵，
∴，
∴，
∴；
（2）解：①若，
则，，
由可得：，
∴，
由可得：，
∴；
②若，
则，，
由可得：，
∴，
由可得：，
∴，
综上所述，当与全等时，x和t的值分别为：，或，．
25.
（1）证明：∵∠D+∠DAB+∠ABC+∠DCB＝360°，∠DAB＝60°，∠DCB＝120°，
∴∠D+∠ABC＝360°﹣60°﹣120°＝180°．
又∵∠CBF+∠ABC＝180°，∴∠D＝∠CBF．
在△CDE和△CBF中， ，
∴△CDE≌△CBF（SAS）．∴CE＝CF．
（2）解：猜想DE、EG、BG之间的数量关系为：DE+BG＝EG．理由如下：
连接AC，如图所示．
在△ABC和△ADC中， ，
∴△ABC≌△ADC（SSS），
∴∠BCA＝∠DCA＝∠DCB＝×120°＝60°．
又∵∠ECG＝60°，
∴∠DCE＝∠ACG，∠ACE＝∠BCG．
由（1）可得：△CDE≌△BDF，
∴∠DCE＝∠BCF．
∴∠BCG+∠BCF＝60°，即∠FCG＝60°．
∴∠ECG＝∠FCG．
在△CEG和△CFG中， ，
∴△CEG≌△CFG（SAS），
∴EG＝FG．
又∵DE＝BF，FG＝BF+BG，
∴DE+BG＝EG．