初中数学沪教版（五四制）（2024）六年级上册（2024）第1章 有理数1.2 有理数的加法与减法授课ppt课件

这是一份初中数学沪教版（五四制）（2024）六年级上册（2024）第1章 有理数1.2 有理数的加法与减法授课ppt课件，共18页。PPT课件主要包含了+-6-3等内容，欢迎下载使用。

（1）探索、理解、掌握有理数的减法法则，发展抽象能力、推理能力；（2）通过把减法转化为加法，体会转化与化归思想；（3）会利用有理数的减法解决实际问题，提升应用意识。
有理数的减法的运算法则，以及法则的应用。
有理数减法法则的推导，发展学生逻辑思维能力。
同样的，有理数的减法是有理数加法的逆运算。
有理数的减法就是已知两个有理数的和与其中的一个加数，求另一个加数的运算。
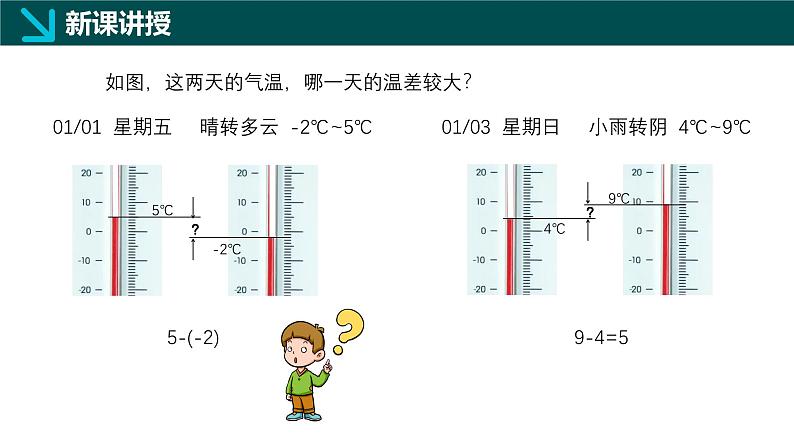
如图，这两天的气温，哪一天的温差较大？
01/01 星期五 晴转多云 -2℃~5℃
01/03 星期日 小雨转阴 4℃~9℃
如何求5-(-2)呢？
减法是加法的逆运算，计算5-(-2)，就是要求出一个数，使这个数与(-2)相加得5.
因为7+(-2)=5,所以5-(-2)=7
又因为5+2=7，所以
5-(-2)=5+2.
计算9-4与9+(-4),从中又有什么发现？
有理数的减法法则：减去一个数，等于加上这个数的相反数，即a-b=a+(-b)
分析：根据有理数的减法法则，可以先把有理数的减法转化成加法，然后按照有理数的加法法则进行计算。
(1)6-(-6)=6+6=12
(2)0-9=0+(-9)=-9
例6 计算：-16+7-(-13)-14.
分析：这个算式中既有加法，也有减法，根据有理数的减法法则，可以把它改写成(-16)+7+13+(-14)，使问题转化为几个有理数的加法。
-16+7-(-13)-14=(-16)+7+13+(-14)=[(-16)+(-14)]+(7+13)=(-30)+20=-10.
例7 某大桥桥面再江面上方约48m.求桥面到江底的距离。
解：设江面上方为正，那么48-(-10)=48+10=58(m)
答：桥面到江底的距离为58m。
1.根据有理数减法法则，再下列各题的横线处填上“+”或“-”：
(1)(-4)-(+2)=(-4)+( 2);(2)(-7)-(-6)=(-7)+( 6);(3)3-5=3+( 5);(4)(+8)+(-5)=(+8)-( 5).
(1)(-33)-22
(2)0.5-(-0.5)
(1)(-33)-22=(-33)+(-22)=-(33+22)=-55
(2)0.5-(-0.5)=0.5+0.5=1
(1)(-7)-(+5)+(-4)-(-10)
(1)(-7)-(+5)+(-4)-(-10) =(-7)+(-5)+(-4)+(+10) =-(7+5+4)+10 =-16+10 =-6
4.已知a，b，c三个数在数轴上对应点的位置如图所示，下列几个判断，①a0;④c-a>0;正确的个数是（　　）
A.1 B.2 C.3 D.4
5.下列说法正确的是（    ）A．被减数-减数=差，差一定小于被减数B．绝对值相等的两个数差为0C．减去一个数等于加上这个数的相反数D．0减去一个数，仍得这个数
6.2024年，第33届夏季奥林匹克运动会将在法国巴黎举行．如图，将5个城市的国际标准时间(单位：时)在数轴上表示，那么开幕式的巴黎时间7月26日19时30分对应的是（　）
A．纽约时间7月26日14时30分B．伦敦时间7月26日18时30分C．北京时间7月27日3时30分D．汉城时间7月26日3时30分
7.展览馆某天四个时间段进出馆人数统计如下，则馆内人数变化最大时间段为（    ）A．9∶00～10∶00 B．10∶00～11∶00C．14∶00～15∶00 D．15∶00～16∶00