沪教版（五四制）（2024）六年级上册（2024）1.2 有理数的加法与减法优秀教学ppt课件

这是一份沪教版（五四制）（2024）六年级上册（2024）1.2 有理数的加法与减法优秀教学ppt课件，共26页。PPT课件主要包含了学习目标，情景导入，新知探究，概念归纳，课本例题，课本练习，基础练，易错练，发散思维练，解如图①所示等内容，欢迎下载使用。

1.了解有理数加法的意义，理解有理数加法法则的合理性.2.能运用该法则准确进行有理数的加法运算.(重点）3.经历探索有理数加法法则的过程，理解并掌握有理数加法的法则.（难点）
在小学阶段，我们学习了自然数和正分数的加法运算法则.引人负数后数就扩充到了有理数，那么在有理数范围内如何进行加法运算呢?
思考——已知一家商店五月份的盈亏情况如下；第一个月上半月盈利3万元，下半月盈利2万元;第二个月上半月亏损2万元，下半月亏损1万元;第三个月上半月亏损1万元，下半月盈利3万元;第四个月上半月盈利2万元，下半月亏损2万元;第五个月上半月亏损2万元，下半月盈利1万元.问:这家商店以上各月是盈利还是亏损?每个月盈利或亏损各是多少万元?
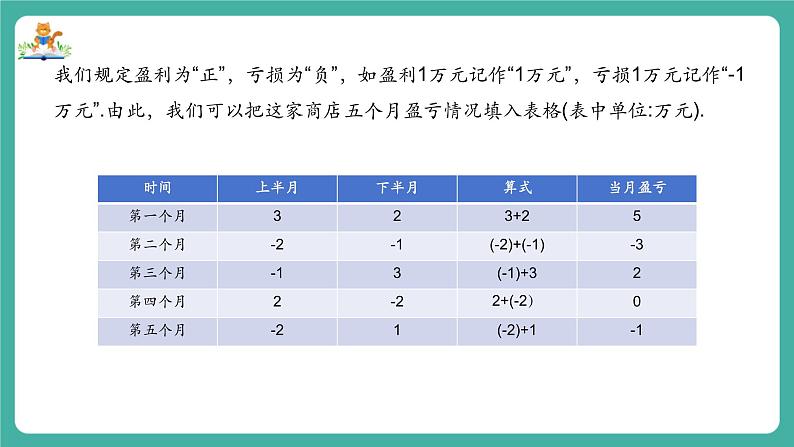
我们规定盈利为“正”，亏损为“负”，如盈利1万元记作“1万元”，亏损1万元记作“-1万元”.由此，我们可以把这家商店五个月盈亏情况填入表格(表中单位:万元).
由表中得到:① 3+2=5，②(-2)+(-1)=-3，③(-1)+3=2,④2+(-2)=0，⑤(-2)+1=-1.从这些算式中，你有什么发现?
有理数的加法法则(1)同号两数相加，取原来加数的符号，并把绝对值相加.(2)异号两数相加，绝对值相等时和为0;绝对值不相等时，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值(3)任何一个数与0相加，仍得这个数.
分析 同号两数相加，取原来加数的符号，并把绝对值相加;一个数与0相加，仍得这个数.
(1)3+(-3); (2)(-16)+5;
分析 异号两数相加，绝对值相等时和为0;绝对值不相等时，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值.
解(1)3(-3)=0.
互为相反数的两个数的和为 0.
(2)(-16)+5=-(16-5)=-11.
解 设向东行驶为正，则向西为负;向东行驶15km和20km分别记作15 km 和 20 km，向西行驶 25 km 记作 -25 km.根据题意，得15+(-25)+20=(-10)+20=10(km)答:卡车最后停在A站东面10km处.
分析 画出示意图，可以看到卡车三次的行驶路程分别为从A到B，从B到C，从C到D，所以点D为卡车最后停止的位置，
例3 已知一辆运货卡车从A站出发，先向东行驶15千米，卸货之后再向西行驶25千米装上另一批货物，然后又向东行驶20千米后停下来，问卡车最后停在何处。
1. 在下列各题的横线处填上“+”或“-”，使下列式子成立:(1)(_6)+(_6)=0 (2)(_7)+(_6)=-13;(3)(_7)+(_6)=1; (4) (_7)+(_6)=-1;
(2)(-13)+(-9);
3.冬天，乐乐家开着空调取暖.在某一时刻，室外的温度是-4℃室内的温度比室外的温度高 23℃，那么这时室内的温度是多少摄氏度?
解:-4+23=19(摄氏度)答:这时室内的温度是19摄氏度
1.（闵行区期中）如果两个数的和是正数，那么( ____ )A.这两个加数都是正数B.一个加数为正数，另一个加数为0C.一个加数为正数，另一个加数为负数，且正数的绝对值大于负数的绝对值D.以上皆有可能
【解析】解：如果两个数的和是正数，可能这两个加数都是正数，如1+1=2，可能一个数为正数，另一个加数为0，如0+2=2，可能一个加数为正数，另一个加数为负数，且正数的绝对值大于负数的绝对值，如-1+3=2，故选：D．
2.（松江区期中）计算：2+(-5)= ____ ．
【解析】解：原式=-(5-2)=-3．故答案为：-3．
4.（2024春•浦东新区期末）计算：1.4+(-2.6)= ______ ．
【解析】解：1.4+(-2.6)=-1.2．故答案为：-1.2．
计算时因考虑问题不全而漏解8. [新考法·逆向思维法]马小哈在计算一道有理数运算｜(－3)＋■｜时，一不小心将墨水泼在作业本上了，其中“■”是被墨水污染看不清的一个数，他便问同桌，同桌故弄玄虚地说：“该题计算的结果等于6.”那么被墨水遮住的数是(　D　)
【解析】因为｜(－3)＋■｜＝6，所以(－3)＋■＝±6.所以■ ＝－3或9.故选D.
题型1.利用有理数的加法法则计算
【解】原式＝(－3.6)＋(－2.71)＋(＋1.69)＝(－6.31)＋1.69＝－4.62.
【解】原式＝｜－5.5＋4.25｜＋(－7＋5.5)＝1.25＋(－1.5)＝－0.25.
题型2.利用有理数加法法则求值
10. (1)已知｜ x ｜＝6，｜ y ｜＝11，求 x ＋ y 的值；
【解】因为｜ x ｜＝6，所以 x ＝±6.因为｜ y ｜＝11，所以 y ＝±11.当 x ＝6， y ＝11时， x ＋ y ＝17；当 x ＝6， y ＝－11时， x ＋ y ＝－5；当 x ＝－6， y ＝11时， x ＋ y ＝5；当 x ＝－6， y ＝－11时， x ＋ y ＝－17.综上， x ＋ y 的值为17，－5，5或－17.
11.（2023秋•徐汇区校级月考）在CCTV“开心辞典”栏目中，主持人问这样一道题目：a是-[-(-2)]的相反数，b是最大的负整数，c是绝对值最小的有理数，则a+b+c= ____ ．
【解析】解：由题意得：a=2，b=-1，c=0，∴a+b+c=2+(-1)+0=1，故答案为：1．
题型3.利用有理数加法法则解实际应用
12. 【情境题·生活应用】某出租车驾驶员从公司出发，在南北向的人民路上连续接送5批客人，行驶路程记录如下(规定向南为正，向北为负，单位：km)：
(1)接送完第5批客人后，该驾驶员在公司什么方向，距离公司多少千米？
解：(1)5＋2＋(－4)＋(－3)＋6＝6(km).答：接送完第5批客人后，该驾驶员在公司的南边，距离公司6 km.
(2)若该出租车每千米耗油0.3 L，那么在这过程中共耗油多少升？
解：(2)(5＋2＋｜－4｜＋｜－3｜＋6)×0.3＝20×0.3＝6(L).答：在这个过程中共耗油6 L.
(3)若该出租车的计价标准为：行驶路程不超过3 km收费8元，超过3 km的部分按每千米加1.8元收费，在这过程中该驾驶员共收到车费多少元？
解：(3)[8＋(5－3)×1.8]＋8＋[8＋(｜－4｜－3)×1.8] ＋8＋[8＋(6－3)×1.8]＝50.8(元).
答：在这个过程中该驾驶员共收到车费50.8元.
13. [情境题·趣味数学]还记得小时候经常玩的填数游戏吗？ 一起用有理数来试试吧！
(1)请在图①的各个圆圈内填上适当的数，使每个圆圈内 的数都等于与它相邻的2个数的和.
(2)如图②，在圆圈内填上恰当的数，使每条线上的3个 数之和为0.
【解】如图②所示(答案不唯一).
(3)将图②中心处的0改为－5，如图③，在圆圈内填上适 当的数，使每条线上的3个数之和为－15.
【解】如图③所示(答案不唯一).
14. [新考法·特殊到一般的思想](1)比较大小：
①｜－2｜＋｜3｜ ｜－2＋3｜；
②｜4｜＋｜3｜ ｜4＋3｜；
④｜－5｜＋｜0｜ ｜－5＋0｜.
(2)通过(1)中的大小比较，猜想并归纳出｜ a ｜＋｜ b ｜与｜ a ＋ b ｜的大小关系，并说明当 a ， b 满足什么关系时，｜ a ｜＋｜ b ｜＝｜ a ＋ b ｜成立.
【解】｜ a ｜＋｜ b ｜≥｜ a ＋ b ｜.当 ab ≥0时，｜ a ｜＋｜ b ｜＝｜ a ＋ b ｜成立.
(3)根据(2)中得出的结论，当｜ x ｜＋2 026＝｜ x ＋2026｜时， x 的取值范围是 ⁠.