

2024年山东省滨州市中考数学模拟试题(四)
展开一、单选题
1.计算的结果,正确的是( )
A.B.C.D.
2.下列新能源汽车标志图案中,既是轴对称图形,又是中心对称图形的是( )
A.B.C.D.
3.无色酚酞溶液是一中常见常用酸碱指示剂,广泛应用于检验溶液酸碱性,通常情况下酚酞溶液遇酸溶液不变色,遇中性溶液也不变色,遇碱溶液变红色.现有5瓶缺失标签的无色液体:蒸馏水、白醋溶液、食用碱溶液、柠檬水溶液、火碱溶液,将酚酞试剂滴入任意一瓶液体后呈现红色的概率是( )
A.B.C.D.
4.若关于x的方程无解,则m的值为( )
A.0B.4或6C.6D.0或4
5.甲、乙两车从城出发前往城,在整个行程中,汽车离开A城的距离y(单位:km)与时间x(单位:h)的对应关系如图所示.下列说法中不正确的是( )
A.甲车行驶到距城240km处,被乙车追上
B.A城与B城的距离是300km
C.乙车的平均速度是80km/h
D.甲车比乙车早到B城
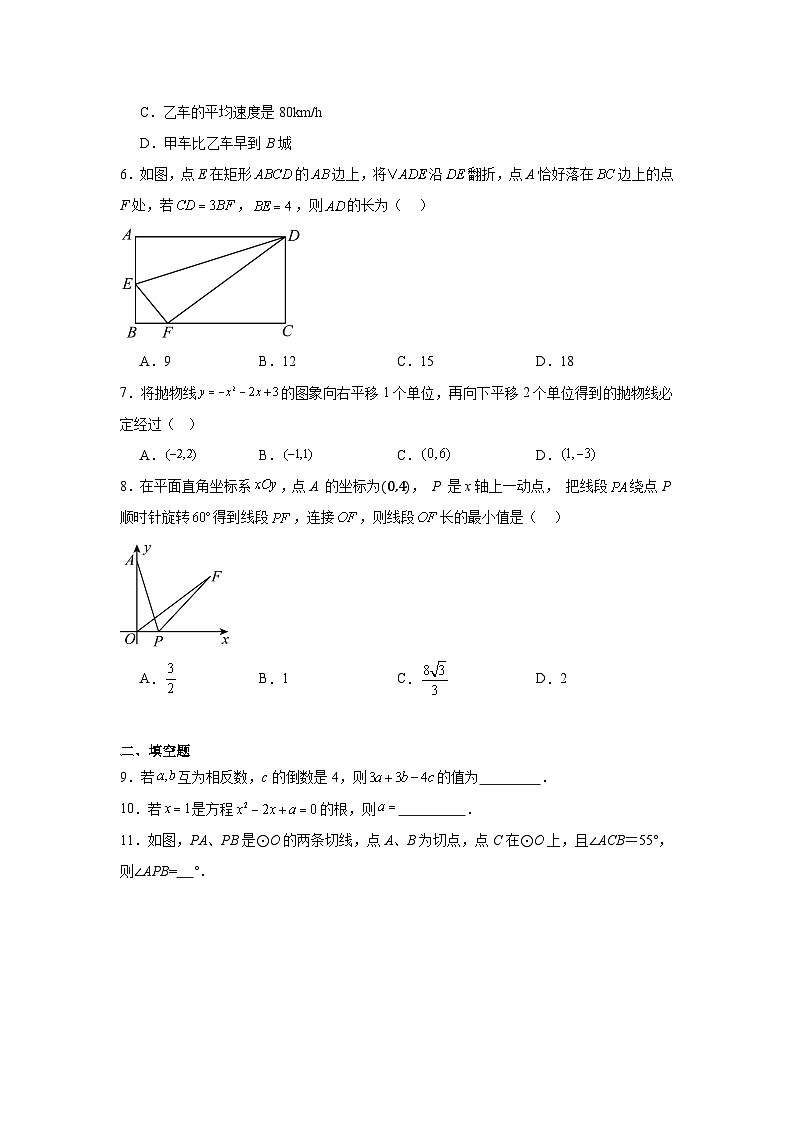
6.如图,点E在矩形的边上,将沿翻折,点A恰好落在边上的点F处,若,,则的长为( )
A.9B.12C.15D.18
7.将抛物线的图象向右平移1个单位,再向下平移2个单位得到的抛物线必定经过( )
A.B.C.D.
8.在平面直角坐标系,点A 的坐标为0,4, P 是x轴上一动点, 把线段绕点P顺时针旋转得到线段,连接,则线段长的最小值是( )
A.B.1C.D.2
二、填空题
9.若互为相反数,c的倒数是4,则的值为 .
10.若是方程的根,则 .
11.如图,PA、PB是⊙O的两条切线,点A、B为切点,点C在⊙O上,且∠ACB=55°,则∠APB= °.
12.如图是钉板示意图,每相邻4个钉点是边长为1个单位长的小正方形顶点,钉点A,B的连线与钉点C,D的连线交于点E,则
(1)AB与CD是否垂直? (填“是”或“否”);
(2)AE= .
13.如图,在中,,以点A为圆心、为半径画弧交于点E,连接,若,则图中阴影部分的面积是 .
14.在中, 则 .
15.“勾股树”是以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程所画出来的图形,因为重复数次后的形状好似一棵树而得名.假设如图分别是第一代勾股树、第二代勾股树、第三代勾股树,按照勾股树的作图原理作图,则第六代勾股树中正方形的个数为 .
16.如图,在矩形ABCD中,,E,F分别是AD,AB的中点,的平分线交AB于点G,点P是线段DG上的一个动点,则的周长最小值为 .
三、解答题
17.某市教育局为了解“双减”政策落实情况,随机抽取几所学校部分初中生进行调查,统计他们平均每天完成作业的时间,并根据调查结果绘制如下不完整的统计图:
请根据图表中提供的信息,解答下面的问题:
(1)在调查活动中,教育局采取的调查方式是___________(填写“普查”或“抽样调查”);
(2)教育局抽取的初中生有___________人,扇形统计图中m的值是___________;
(3)已知平均每天完成作业时长在“”分钟的9名初中生中有5名男生和4名女生,若从这9名学生中随机抽取一名进行访谈,且每一名学生被抽到的可能性相同,则恰好抽到男生的概率是___________;
(4)若该市共有初中生10000名,则平均每天完成作业时长在“”分钟的初中生约有___________人.
18.先化简,再求值:,请从不等式组 的整数解中选择一个合适的数求值.
19.小明带10元钱想买一盒饼干和一袋牛奶,可是售货员阿姨说:本来10元钱够一盒饼干的,但再买一袋牛奶就不够了,今天是儿童节给你的饼干打9折,两样东西拿好,再找你8角钱,饼干的标价可是整数哦,请你帮小明算出牛奶和饼干的标价.
20.2022年我国已成为全球最大的电动汽车市场,电动汽车在保障能源安全,改善空气质量等方面较传统汽车都有明显优势,经过对某款电动汽车和某款燃油车的对比调查发现,电动汽车平均每公里的充电费比燃油车平均每公里的加油费少0.6元.若充电费和加油费均为200元时,电动汽车可行驶的总路程是燃油车的4倍,求这款电动汽车平均每公里的充电费.
21.如图,在中,交于点,点在上,.
(1)求证:四边形是平行四边形;
(2)若求证:四边形是菱形.
22.如图,BD是矩形ABCD的对角线.
(1)求作⊙A,使得⊙A与BD相切(要求:尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,设BD与⊙A相切于点E,CF⊥BD,垂足为F.若直线CF与⊙A相切于点G,求的值.
23.综合与实践
综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.
(1)操作判断
操作一:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平;
操作二:在AD上选一点P,沿BP折叠,使点A落在矩形内部点M处,把纸片展平,连接PM,BM.
根据以上操作,当点M在EF上时,写出图1中一个30°的角:______.
(2)迁移探究
小华将矩形纸片换成正方形纸片,继续探究,过程如下:
将正方形纸片ABCD按照(1)中的方式操作,并延长PM交CD于点Q,连接BQ.
①如图2,当点M在EF上时,∠MBQ=______°,∠CBQ=______°;
②改变点P在AD上的位置(点P不与点A,D重合),如图3,判断∠MBQ与∠CBQ的数量关系,并说明理由.
(3)拓展应用
在(2)的探究中,已知正方形纸片ABCD的边长为8cm,当FQ=1cm时,直接写出AP的长.
参考答案:
1.B
【分析】化简二次根式并代入特殊角的锐角三角比,再按照正确的运算顺序进行计算即可.
【详解】解:
=
=
=.
故选:B
【点睛】此题考查了二次根式的运算、特殊角的锐角三角比等知识,熟练掌握运算法则是解题的关键.
2.A
【分析】根据中心对称图形与轴对称图形的概念进行判断即可.
【详解】A.既是轴对称图形,又是中心对称图形,故A符合题意;
B.是轴对称图形,不是中心对称图形,故B不符合题意;
C.不是轴对称图形,是中心对称图形,故C不符合题意;
D.是轴对称图形,不是中心对称图形,故D不符合题意.
故选:A.
【点睛】本题考查的是中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后与自身重合.
3.B
【分析】根据概率公式求解即可.
【详解】解:∵酚酞溶液遇酸溶液不变色,遇中性溶液也不变色,遇碱溶液变红色,
∵总共有5种溶液,其中碱性溶液有2种,
∴将酚酞试剂滴入任意一瓶液体后呈现红色的概率是:.
故选:B.
【点睛】此题考查了概率的知识,解题的关键是熟练掌握概率的求解方法.
4.D
【分析】先将分时方程化为整式方程,再根据方程无解的情况分类讨论,当时,当时,或,进行计算即可.
【详解】方程两边同乘,得,
整理得,
原方程无解,
当时,;
当时,或,此时,,
解得或,
当时,无解;
当时,,解得;
综上,m的值为0或4;
故选:D.
【点睛】本题考查了分式方程无解的情况,即分式方程有增根,分两种情况,分别是最简公分母为0和化成的整式方程无解,熟练掌握知识点是解题的关键.
5.D
【分析】根据函数图象即可判断.
【详解】由图象可知,A城与B城的距离是300km,故B选项正确;
甲车的速度,,
甲车行驶到距城240km处,被乙车追上,故A选项正确;
乙车的速度,故C选项正确;
乙车比甲车先到达B城,故D选项不正确;
故选:D.
【点睛】本题考查了从函数图象中获取信息,准确理解题意,熟练掌握知识点是解题的关键.
6.C
【分析】根据折叠的性质可得,设,则,则,在中勾股定理建列方程,求得,进而求得,根据,可得,即,求得,在中,勾股定理即可求解.
【详解】解:∵四边形是矩形,
∴,,
将沿翻折,点A恰好落在边上的点F处,
,,
,,
设,则,,
在中,
即,
解得,
,
,,
,
,
,
,
,
在中,,
.
故选C.
【点睛】本题考查了矩形与折叠的性质,正切的定义,勾股定理,掌握折叠的性质以及勾股定理是解题的关键.
7.B
【分析】根据二次函数平移性质“左加右减,上加下减”,得出将抛物线的图象向右平移1个单位,再向下平移2个单位得到的抛物线的解析式,代入求值即可.
【详解】解:将抛物线化为顶点式,
即:
,
将抛物线的图象向右平移1个单位,再向下平移2个单位,
根据函数图像平移性质:左加右减,上加下减得:
,
A选项代入,,不符合;
B选项代入, ,符合;
C选项代入, ,不符合;
D选项代入,,不符合;
故选:B.
【点睛】本题主要考查函数图像平移的性质,一般先将函数化为顶点式:即的形式,然后按照“上加下减,左加右减”的方式写出平移后的解析式,能够根据平移方式写出平移后的解析式是解题关键.
8.D
【分析】本题主要考查等边三角形的判定和性质、全等三角形的判定和性质及旋转的性质.连接,以为边作等边,连接,则,可得是等边三角形,可证明,从而得到,进而得到点P在x轴上运动时,点F在直线上运动,作,交直线于点,于点E,则,即当F在直线上运动到点的位置时,线段取得最小值,即可求解.
【详解】解:连接,以为边作等边,连接,则,
,
∴是等边三角形,
∴,
∴,
在和中,
∵,
∴,
∴,
∴点P在x轴上运动时,点F在直线上运动,
作,交直线于点,于点E,则,
即当F在直线上运动到点的位置时,线段取得最小值,
∴,
∵,,,
∴四边形是矩形,
∴,
即线段的最小值为2.
故选:D
9.
【分析】两数互为相反数,和为0;两数互为倒数,积为1,由此可解出此题.
【详解】解:∵互为相反数,c的倒数是4,
∴,,
∴
.
故答案为:.
【点睛】本题考查的是代数式求值,相反数和倒数的概念,两数互为相反数,则它们的和为0;两数互为倒数,它们的积为1.
10.1
【分析】本题根据一元二次方程的根的定义,把x=1代入方程得到a的值.
【详解】把x=1代入方程,得1−2+a=0,
解得a=1,
故答案为:1.
【点睛】本题考查的是一元二次方程的根即方程的解的定义,一元二次方程的根就是一元二次方程的解,就是能够使方程左右两边相等的未知数的值.
11.70°
【分析】连接OA、OB,根据圆周角定理求得∠AOB,由切线的性质求出∠OAP=∠OBP=90°,再由四边形的内角和等于360°,即可得出答案
【详解】解:连接OA、OB,∠ACB=55°,
∴∠AOB=110°
∵PA、PB是⊙O的两条切线,点A、B为切点,
∴∠OAP=∠OBP=90°
∵∠APB+∠OAP+∠AOB+∠OBP=360°
∴∠APB=360°-(∠OAP+∠AOB+∠OBP)=70°
故答案为:70
【点睛】本题考查了切线的性质、四边形的内角和定理以及圆周角定理,利用切线性质和圆周角定理求出角的度数是解题的关键
12. 是 /
【分析】(1)证明△ACG≌△CFD,推出∠CAG=∠FCD,证明∠CEA=90°,即可得到结论;
(2)利用勾股定理求得AB的长,证明△AEC∽△BED,利用相似三角形的性质列式计算即可求解.
【详解】解:(1)如图:AC=CF=2,CG=DF=1,∠ACG=∠CFD=90°,
∴△ACG≌△CFD,
∴∠CAG=∠FCD,
∵∠ACE+∠FCD=90°,
∴∠ACE+∠CAG=90°,
∴∠CEA=90°,
∴AB与CD是垂直的,
故答案为:是;
(2)AB=2,
∵AC∥BD,
∴△AEC∽△BED,
∴,即,
∴,
∴AE=AB=.
故答案为:.
【点睛】本题考查了相似三角形的判定和性质,全等三角形的判定和性质,解答本题的关键是明确题意,找出所求问题需要的条件.
13.
【分析】过点D作DF⊥AB于点F,根据等腰直角三角形的性质求得DF,从而求得EB,最后由S阴影=S▱ABCD−S扇形ADE−S△EBC结合扇形面积公式、平行四边形面积公式、三角形面积公式解题即可.
【详解】解:过点D作DF⊥AB于点F,
∵,
∴AD=
∴DF=ADsin45°= ,
∵AE=AD=2 ,
∴EB=AB−AE= ,
∴S阴影=S▱ABCD−S扇形ADE−S△EBC
=
故答案为:.
【点睛】本题考查等腰直角三角形、平行四边形的性质、扇形的面积公式等知识,是重要考点,难度较易,掌握相关知识是解题关键.
14.11
【分析】本题主要考查了等腰三角形的判定和性质,勾股定理.在取点D,使,过点A作于点E,则,根据,可得,设,则,根据勾股定理可得关于x的方程,求出x的值,即可求解.
【详解】解:如图,在取点D,使,过点A作于点E,则,
∴,
∵,,
∴,
∴,
设,则,
∵,
∴,
即,
解得:,
即,
∴.
故答案为:11.
15.127
【分析】由已知图形观察规律,即可得到第六代勾股树中正方形的个数.
【详解】解:∵第一代勾股树中正方形有1+2=3(个),
第二代勾股树中正方形有1+2+22=7(个),
第三代勾股树中正方形有1+2+22+23=15(个),
.
∴第六代勾股树中正方形有1+2+22+23+24+25+26=127(个),
故答案为:127.
【点睛】本题考查图形中的规律问题,解题的关键是仔细观察图形,得到图形变化的规律.
16./
【分析】在CD上取点H,使DH=DE,连接EH,PH,过点F作FK⊥CD于点K,可得DG垂直平分EH,从而得到当点F、P、H三点共线时,的周长最小,最小值为FH+EF,再分别求出EF和FH,即可求解.
【详解】解:如图,在CD上取点H,使DH=DE,连接EH,PH,过点F作FK⊥CD于点K,
在矩形ABCD中,∠A=∠ADC=90°,AD=BC=6,CD=AB=8,
∴△DEH为等腰直角三角形,
∵DG平分∠ADC,
∴DG垂直平分EH,
∴PE=PH,
∴的周长等于PE+PF+EF=PH+PF+EF≥FH+EF,
∴当点F、P、H三点共线时,的周长最小,最小值为FH+EF,
∵E,F分别是AD,AB的中点,
∴AE=DE=DH=3,AF=4,
∴EF=5,
∵FK⊥CD,
∴∠DKF=∠A=∠ADC=90°,
∴四边形ADKF为矩形,
∴DK=AF=4,FK=AD=6,
∴HK=1,
∴,
∴FH+EF=,即的周长最小为.
故答案为:
【点睛】本题主要考查了最短距离问题,矩形的判定和性质,勾股定理等知识,明确题意,准确得到当点F、P、H三点共线时,的周长最小,最小值为FH+EF是解题的关键.
17.(1)抽样调查;
(2)300,30
(3)
(4)3000
【分析】(1)根据题目中的“随机抽取几所学校部分初中生进行调查”可以判定是抽样调查;
(2)读图可得,A组有45人,占15%,即可求得总人数;用B组的人数除以总人数再乘100%即可得出答案;
(3)根据概率公式计算即可;
(4)由样本中平均每天完成作业时长在“”分钟的初中生的比例乘以10000人即可;
【详解】(1)根据题目中的“随机抽取几所学校部分初中生进行调查”可以判定是抽样调查;
故答案为:抽样调查;
(2)教育局抽取的初中生人数为:(人)
B组人数为:
∴B组所占的百分比为:
∴
(3)∵9名初中生中有5名男生和4名女生,
∴从这9名学生中随机抽取一名进行访谈,恰好抽到男生的概率是
(4)样本中平均每天完成作业时长在“”分钟的初中生占比
∴该市共有初中生10000名,则平均每天完成作业时长在“”分钟的初中生约有人.
【点睛】本题考查条形统计图和扇形统计图,读懂统计图,从不同的统计图中得到必要的信息是解答本题的关键.
18.,3
【分析】根据分式的加减运算以及乘除运算法则进行化简,然后根据不等式组求出a的值并代入原式即可求出答案.
【详解】解:
,
,
解不等式①得:
解不等式②得:,
∴,
∵a为整数,
∴a取0,1,2,
∵,
∴a=1,
当a=1时,原式.
【点睛】本题考查分式的化简求值,解一元一次不等式组,解题的关键是熟练运用分式的加减运算法则以及乘除运算法则,本题属于基础题型.
19.牛奶和饼干的标价分别为1.1元和9元
【分析】本题主要考查了一元一次方程,掌握不等式和方程的解法,根据题意列出方程和不等式是解决本题的关键.
根据题意先列出方程和不等式,求解即可.
【详解】解:设饼干的标价是元,牛奶的标价是元.
由题意,得,
解得.
由于饼干的标价是整数,
所以(元).
当时,(元).
答:牛奶和饼干的标价分别为1.1元和9元.
20.这款电动汽车平均每公里的充电费为0.2元.
【分析】设这款电动汽车平均每公里的充电费为x元,则燃油车平均每公里的充电费为(x+0.6)元,根据“电动汽车可行驶的总路程是燃油车的4倍”列分式方程,解方程即可求解.
【详解】解:设这款电动汽车平均每公里的充电费为x元.
根据题意,得.
解,得.
经检验,是原方程的根.
答:这款电动汽车平均每公里的充电费为0.2元.
【点睛】本题考查分式方程的应用,分析题意,找到合适的等量关系是解决问题的关键.
21.(1)见解析
(2)见解析
【分析】(1)先根据四边形ABCD为平行四边形,得出,,再根据,得出,即可证明结论;
(2)先证明,得出,证明四边形ABCD为菱形,得出,即可证明结论.
【详解】(1)证明:∵四边形ABCD为平行四边形,
∴,,
∵,
∴,
即,
∴四边形是平行四边形.
(2)∵四边形ABCD为平行四边形,
∴,
∴,
∵
∴,
∴,
∴四边形ABCD为菱形,
∴,
即,
∵四边形是平行四边形,
∴四边形是菱形.
【点睛】本题主要考查了平行四边形的判定和性质,菱形的判定和性质,平行线的性质,熟练掌握菱形和平行四边形的判定方法,是解题的关键.
22.(1)作图见解析
(2)
【分析】(1)先过点A作BD的垂线,进而找出半径,即可作出图形;
(2)根据题意,作出图形,设,⊙A的半径为r,先判断出BE=DE,进而得出四边形AEFG是正方形,然后在Rt△ABE中,根据勾股定理建立方程求解,再判定,根据,,在Rt△ADE中,利用,得到,求解得到tan∠ADB的值为.
【详解】(1)解:如图所示,⊙A即为所求作:
(2)解:根据题意,作出图形如下:
设,⊙A的半径为r,
∵BD与⊙A相切于点E,CF与⊙A相切于点G,
∴AE⊥BD,AG⊥CG,即∠AEF=∠AGF=90°,
∵CF⊥BD,
∴∠EFG=90°,
∴四边形AEFG是矩形,
又,
∴四边形AEFG是正方形,
∴,
在Rt△AEB和Rt△DAB中,,,
∴,
在Rt△ABE中,,
∴,
∵四边形ABCD是矩形,
∴,AB=CD,
∴,又,
∴,
∴,
∴,
在Rt△ADE中,,即,
∴,即,
∵,
∴,即tan∠ADB的值为.
【点睛】此题是圆的综合题,主要考查了尺规作图,切线的性质,全等三角形的判定和性质,正方形的判定与性质,矩形的判定与性质,勾股定理,锐角三角函数,利用三角函数得出线段长建立方程是解决问题的关键.
23.(1)或或或
(2)①15,15;②,理由见解析
(3)cm或
【分析】(1)根据折叠的性质,得,结合矩形的性质得,进而可得;
(2)根据折叠的性质,可证,即可求解;
(3)由(2)可得,分两种情况:当点Q在点F的下方时,当点Q在点F的上方时,设分别表示出PD,DQ,PQ,由勾股定理即可求解.
【详解】(1)解:
,sin∠BME=
(2)∵四边形ABCD是正方形
∴AB=BC,∠A=∠ABC=∠C=90°
由折叠性质得:AB=BM,∠PMB=∠BMQ=∠A=90°
∴BM=BC
①
∴
②
(3)当点Q在点F的下方时,如图,
,DQ=DF+FQ=4+1=5(cm)
由(2)可知,
设
,
即
解得:
∴;
当点Q在点F的上方时,如图,
cm,DQ =3cm,
由(2)可知,
设
,
即
解得:
∴.
【点睛】本题主要考查矩形与折叠,正方形的性质、勾股定理、三角形的全等,掌握相关知识并灵活应用是解题的关键.
题号
1
2
3
4
5
6
7
8
答案
B
A
B
D
D
C
B
D
2024年山东省滨州市中考数学模拟试题(四): 这是一份2024年山东省滨州市中考数学模拟试题(四),共20页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2024年山东省滨州市中考数学模拟试卷(四): 这是一份2024年山东省滨州市中考数学模拟试卷(四),共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
山东省滨州市2024年初中学业水平考试数学模拟试题(四): 这是一份山东省滨州市2024年初中学业水平考试数学模拟试题(四),共4页。试卷主要包含了答卷前,考生务必用0,第Ⅱ卷必须用0,若 x=1是方程等内容,欢迎下载使用。












