





初中数学青岛版(2024)九年级上册3.6 弧长及扇形面积的计算优秀ppt课件
展开学习目标:1.理解弧长和扇形面积公式的探求过程.2.会利用弧长和扇形面积的计算公式进行计算.
重点:探索弧长计算方法和扇形面积计算方法.
难点:会利用弧长和扇形面积的计算公式进行计算.
我们在小学学习了圆的面积和扇形的面积,也学习了圆的周长和面积,那么圆上一部分的长,也就是一条弧的长怎么去求呢?现在重新学习圆的面积和扇形面积,比以前是不是有了更深的要求呢? 下面我们就来学习本节内容.
问题1 :如图,在运动会的4×100米比赛中,甲和乙分别在第1跑道和第2跑道,为什么他们的起跑线不在同一处?
问题2:怎样来计算弯道的“展直长度”?
因为要保证这些弯道的“展直长度”是一样的.
我们知道,弧是圆的一部分,弧长就是圆周长的一部分.想一想,如何计算圆的周长?圆的周长可以看作多少度的圆心角所对的弧长?那么,1的圆心角所对的弧长是多少?n的圆心角所对的弧长是多少?
1的圆心角所对的弧长为:
2的圆心角所对的弧长为:
3的圆心角所对的弧长为:
n的圆心角所对的弧长为:
由此,你发现了什么?与同学交流.
在半径为r的扇形中,n的圆心角所对的扇形面积为:
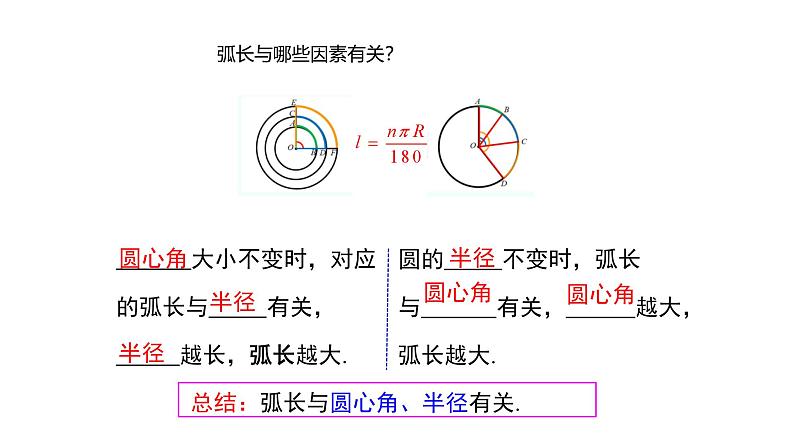
大小不变时,对应的弧长与 有关, 越长,弧长越大.
圆的 不变时,弧长与 有关, 越大,弧长越大.
2. 某扇形的圆心角为 72°,面积为 5π,则此扇形的弧长为 ( )A.π B.2π C.3π D.4π
1. 75° 的圆心角所对的弧长是 2.5π cm,则此弧所在圆的半径是_____cm.
扇形就是圆的一部分,扇形面积就是圆面积的一部分,在半径为R的圆中,360的圆心角所对的扇形面积就是
1的圆心角所对的扇形面积为:
类比弧长,探究新知.
2的圆心角所对的扇形面积为:
3的圆心角所对的扇形面积为:
n的圆心角所对的扇形面积为:
由此你发现了什么?有同学交流
在半径为R的扇形中,n的圆心角所对的扇形面积为:
圆心角是 n° 所对的弧长公式和扇形的面积公式之间的关系.
思考:扇形的面积与哪些因素有关?
大小不变时,对应的扇形面积与 有关, 越长,面积越大.
圆的 不变时,扇形面积与 有关, 越大,面积越大.
例 如图 一把扇形纸扇完全打开后,外侧两竹条AB与AC的夹角为120°,AB的长为30cm,竹条AB上贴纸部分BD的宽为20cm.求扇子的一面上贴纸部分的面积(精确到0.1cm2).
解:由图可知,扇形的圆心为A,圆心角n=120 °,AB=30cm,BD=20cm,图上贴纸部分的面积等于两个扇形面积之差,由扇形的面积公式,贴纸部分的面积为
所以,扇子的一面上贴纸部分的面积约为837.8cm2
1. 已知扇形的半径为 2 cm,其弧长为 cm,则这个扇形的面积 S = .
2. 已知扇形的圆心角为 120°,半径为 2,则这个扇形的面积 S = .
1.已知圆心角为60°,半径为3cm的扇形的弧长为 ( )
2.已知圆心角为900,半径为2的扇形的面积为 ( )
A.2πcm B.πcm C. cm D. cm
A.π B. C. 2π D.
3.一个扇形的圆心角为90°,面积是4πcm2,则该扇形的半径为 .
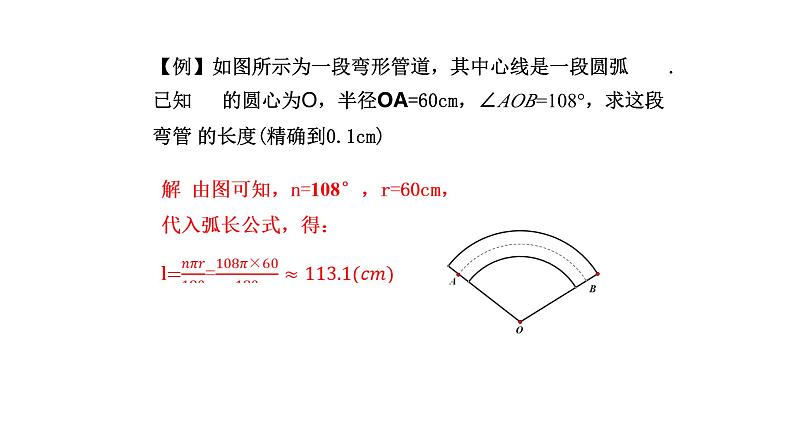
5.制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度l.(单位:mm,精确到1mm)
解:由弧长公式,可得弧AB的长
因此所要求的展直长度l=2×700+1570=2970(mm).
答:管道的展直长度为2970mm.
6.如图,已知扇形AOB的半径为2,圆心角为90°,连接AB,则图中阴影部分的面积是 ( ) A.π-2 B.π-4 C.4π-2 D.4π-4
7. 如图,水平放置的圆柱形排水管道的截面半径是0.6 m,其中水面高0.3 m,求截面上有水部分的面积 (结果保留小数点后两位).
分析:有水部分的面积 = S扇形OAB- S△OAB
∵ OC=0.6 m, DC=0.3 m ,∴ OD= OC-DC=0.3 (m).∴ OD= DC.又 ∵ AD⊥OC ,∴ AD垂直平分OC.
在Rt△OAD中,利用勾股定理,得
∴ AC=AO=OC.从而∠AOD=60°,∠AOB=120°.
S = S扇形OAB- S△OAB
答:截面上有水部分的面积约为0.22 m2.
弓形的面积=扇形的面积±三角形的面积
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
青岛版(2024)九年级上册第3章 对圆的进一步认识3.7 正多边形与圆评优课课件ppt: 这是一份青岛版(2024)九年级上册<a href="/sx/tb_c99065_t3/?tag_id=26" target="_blank">第3章 对圆的进一步认识3.7 正多边形与圆评优课课件ppt</a>,共31页。PPT课件主要包含了课堂导入,探究新知,正多边形的性质,课堂练习等内容,欢迎下载使用。
初中数学青岛版(2024)九年级上册第3章 对圆的进一步认识3.3 圆周角获奖课件ppt: 这是一份初中数学青岛版(2024)九年级上册<a href="/sx/tb_c75360_t3/?tag_id=26" target="_blank">第3章 对圆的进一步认识3.3 圆周角获奖课件ppt</a>,共26页。PPT课件主要包含了课堂导入,探究新知,猜想-----验证,圆周角和圆心角的关系,课堂练习等内容,欢迎下载使用。
初中数学2.2 30°,45°,60°角的三角比示范课课件ppt: 这是一份初中数学<a href="/sx/tb_c99058_t3/?tag_id=26" target="_blank">2.2 30°,45°,60°角的三角比示范课课件ppt</a>,共24页。PPT课件主要包含了sinA,cosA,tanA,课堂导入,合作探究,探究新知,另一条直角边长,小游戏,练一练,解原式等内容,欢迎下载使用。














