

人教A版(2019)必修第二册期中考试测试(基础)(原卷版+解析)
展开2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、单项选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(2023·陕西咸阳)复数 满足(为虚数单位),则的虚部为( )
A.B.C.D.
2.(2023·陕西安康·)如图,在矩形中,是的中点,若,则( )
A.B.1C.D.2
3.(2023安徽芜湖)在△ABC中,,,,则( )
A.B.C.D.或
4.(2023陕西)已知向量,,若向量,则实数的值是( ).
A.B.C.D.2
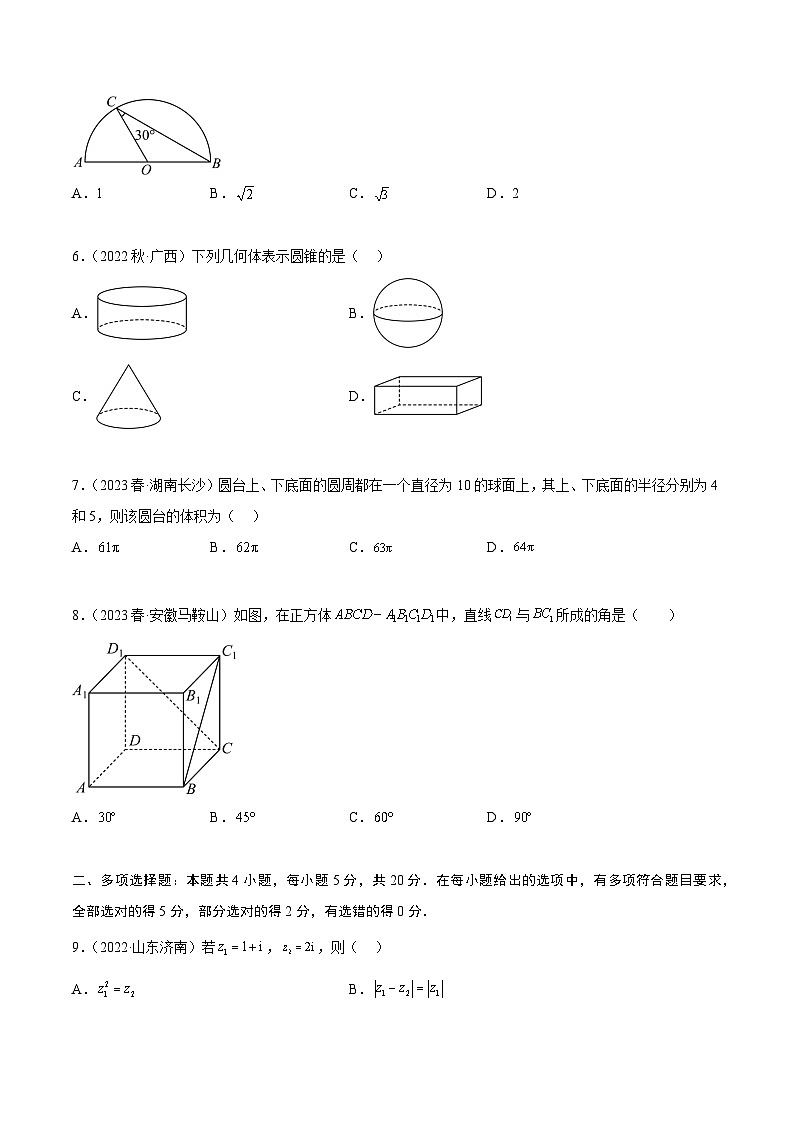
5.(2023春·安徽合肥)在如图所示的半圆中,AB为直径,点O为圆心,C为半圆上一点,且,,则等于( )
A.1B.C.D.2
6.(2022秋·广西)下列几何体表示圆锥的是( )
A.B.
C.D.
7.(2023春·湖南长沙)圆台上、下底面的圆周都在一个直径为10的球面上,其上、下底面的半径分别为4和5,则该圆台的体积为( )
A.B.C.D.
8.(2023春·安徽马鞍山)如图,在正方体中,直线与所成的角是( )
A.B.C.D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
9.(2022·山东济南)若,,则( )
A.B.
C.在复平面内对应的点在第二象限D.是实数
10.(2023春·安徽铜陵)下列四式可以化简为的是( )
A.B.
C.D.
11.(2023·全国·高一专题练习)在中,角所对的边分别为,已知,则下列判断中正确的是( )
A.若,则B.若,则该三角形有两解
C.周长有最大值12D.面积有最小值
12.(2022秋·河北沧州)如图所示,已知几何体是正方体,则( )
A.平面
B.平面
C.异面直线与所成的角为60°
D.异面直线与所成的角为90°
三、填空题:本题共4小题,每小题5分,共20分.
13.(2023上海)如图,是的斜二测直观图,其中,斜边,则的面积是______.
14.(江西省赣州市2023届)已知向量,.若,则实数的值为______.
15.(2022·四川成都·高一统考期中)如图,小李开车在一条水平的公路上向正西方向前进,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶1200m后到达B处,测得此山顶在西偏北75°的方向上,仰角为45°,则此山的高度为______m
16.(2023春·河南)在中,角,,的对边分别为,,,,,则__________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(2022·高一课时练习)(10分)已知复数.
(1)若复数z是实数,求实数a的值;
(2)若复数z是虚数,求实数a的取值范围;
(3)复数z是不是纯虚数?若是纯虚数,求出实数a的值;若不是纯虚数,请说明理由.
18.(2023春·河北)(12分)已知的三个内角所对的边分别是,且.
(1)求的周长;
(2)求边上的高.
19.(2023春·湖南岳阳)(12分)在中,角的对边分别为,且满足.
(1)求角的值;
(2)若,求的面积.
20.(2022秋·辽宁沈阳·高一沈阳二十中校考期末)(12分)已知向量,求:
(1)若,且,求的坐标;
(2)若﹐求;
(3)若,求k的值.
21.(2023·江西南昌·)(12分)已知直棱柱的底面ABCD为菱形,且,,点为的中点.
(1)证明:平面;
(2)求三棱锥的体积.
22.(2023·云南昆明)如图①:在△ABC中,AB=BC=5,∠ABC=90°,DE∥BC,DE=2,将△ADE沿DE折起到△PDE的位置(如图②),且∠PEB=60°.
(1)请作出平面PBC与平面PDE的交线l(不需要说明理由)
(2)证明;平面PBC⊥平面PBE;
(3)求直线PE与平面PBC所成角的正弦值.
期中考试测试(基础)
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、单项选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(2023·陕西咸阳)复数 满足(为虚数单位),则的虚部为( )
A.B.C.D.
【答案】D
【解析】,则复数的虚部为. 故选:D
2.(2023·陕西安康·)如图,在矩形中,是的中点,若,则( )
A.B.1C.D.2
【答案】C
【解析】,∴,,∴,故选:C.
3.(2023安徽芜湖)在△ABC中,,,,则( )
A.B.C.D.或
【答案】B
【解析】由正弦定理得,所以,
由于,所以为锐角,所以.故选:B
4.(2023陕西)已知向量,,若向量,则实数的值是( ).
A.B.C.D.2
【答案】B
【解析】,解得.故选:B
5.(2023春·安徽合肥)在如图所示的半圆中,AB为直径,点O为圆心,C为半圆上一点,且,,则等于( )
A.1B.C.D.2
【答案】A
【解析】如图,连接AC,由,得.
因为为半圆上的点,所以,所以.
故选:A.
6.(2022秋·广西)下列几何体表示圆锥的是( )
A.B.
C.D.
【答案】C
【解析】A图表示圆柱,B图表示球,C图表示圆锥,D图表示四棱柱.故选:C.
7.(2023春·湖南长沙)圆台上、下底面的圆周都在一个直径为10的球面上,其上、下底面的半径分别为4和5,则该圆台的体积为( )
A.B.C.D.
【答案】A
【解析】求得直径为,半径为,圆台的下底面半径为,所以圆台的高为,
所以圆台的体积为.故选:A
8.(2023春·安徽马鞍山)如图,在正方体中,直线与所成的角是( )
A.B.C.D.
【答案】C
【解析】连接,,在正方体中,
因为,且,所以四边形为平行四边形,所以,则即为直线与所成的角或其补角,由正方体的性质可得:为正三角形,所以,则直线与所成的角是,
故选:.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
9.(2022·山东济南)若,,则( )
A.B.
C.在复平面内对应的点在第二象限D.是实数
【答案】ABD
【解析】因为,所以A正确;
因为,,所以B正确;
因为,它在复平面内对应的点为,所以在复平面内对应的点在第一象限,所以C错误;
因为,所以是实数,所以D正确.
故选:ABD.
10.(2023春·安徽铜陵)下列四式可以化简为的是( )
A.B.
C.D.
【答案】ABC
【解析】对选项A:,正确;
对选项B:,正确;
对选项C:,正确;
对选项D:,错误.
故选:ABC
11.(2023·全国·高一专题练习)在中,角所对的边分别为,已知,则下列判断中正确的是( )
A.若,则B.若,则该三角形有两解
C.周长有最大值12D.面积有最小值
【答案】ABC
【解析】对于A,,,由正弦定理得
所以,故A正确;
对于B,由正弦定理得得,所以,
因为有两个解,
所以该三角形有两解,故B正确;
对于C,由,得
,
所以,当且仅当时取等号,此时三角形周长最大为等边三角形,周长为12,故C对;
对于D,由得,
故
由于,
无最小值,
所以面积无最小值,有最大值为,故D错误.
故选:ABC
12.(2022秋·河北沧州)如图所示,已知几何体是正方体,则( )
A.平面
B.平面
C.异面直线与所成的角为60°
D.异面直线与所成的角为90°
【答案】BC
【解析】对于A,由几何体是正方体可知,而平面,
故平面相交,故A错误;
对于B,平面平面,且平面,
所以平面,故B正确;
对于C,,与均为正方体面对角线,故,
三角形是等边三角形,
则直线与所成的角为60°,故C正确;
对于D,,
同理,三角形是等边三角形,
直线与所成的角为60°,故D错误.
故选:BC.
三、填空题:本题共4小题,每小题5分,共20分.
13.(2023上海)如图,是的斜二测直观图,其中,斜边,则的面积是______.
【答案】
【解析】由的斜二测直观图还原得的直观图如下,
因为在中,,,,所以,
则在中,,,,
所以的面积为.
故答案为:.
14.(江西省赣州市2023届)已知向量,.若,则实数的值为______.
【答案】
【解析】因为,,所以,
又因为,所以,
所以.故答案为: .
15.(2022·四川成都·高一统考期中)如图,小李开车在一条水平的公路上向正西方向前进,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶1200m后到达B处,测得此山顶在西偏北75°的方向上,仰角为45°,则此山的高度为______m
【答案】
【解析】由题,作出空间图形如下,
则有,
因为到达B处仰角为45°,所以,
在中,,
由正弦定理可得解得m,
所以m,
故答案为: .
16.(2023春·河南)在中,角,,的对边分别为,,,,,则__________.
【答案】
【解析】∵,∴由正弦定理,得;
又∵,
∴由正弦定理,得,
将代入上式,化简整理得,
两边同除以,得,
解得或(舍).
故答案为:.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(2022·高一课时练习)(10分)已知复数.
(1)若复数z是实数,求实数a的值;
(2)若复数z是虚数,求实数a的取值范围;
(3)复数z是不是纯虚数?若是纯虚数,求出实数a的值;若不是纯虚数,请说明理由.
【答案】(1);
(2);
(3)不是,理由见解析.
【解析】(1)若复数z是实数,则,即,所以;
(2)若复数z是虚数,则,即,所以实数a的取值范围为;
(3)复数z不是纯虚数.理由如下:若复数z是纯虚数,
则,即,此时无解,故复数z不是纯虚数.
18.(2023春·河北)(12分)已知的三个内角所对的边分别是,且.
(1)求的周长;
(2)求边上的高.
【答案】(1)9
(2)
【解析】(1)在△中,,
由余弦定理得,
解得,
∴△的周长为.
(2)∵,∴.
设边上的高为,则,即,
解得.
所以AB边上的高为.
19.(2023春·湖南岳阳)(12分)在中,角的对边分别为,且满足.
(1)求角的值;
(2)若,求的面积.
【答案】(1);
(2).
【解析】(1)解:由题意知,
在中,将正弦定理代入有,
所以,
即,即,
即,
因为,所以,所以,
因为,
所以;
(2)由(1)知,在中,由余弦定理可知,
即,
解得或(舍),
所以.
20.(2022秋·辽宁沈阳·高一沈阳二十中校考期末)(12分)已知向量,求:
(1)若,且,求的坐标;
(2)若﹐求;
(3)若,求k的值.
【答案】(1)或
(2)
(3)
【解析】(1)设,
由,且,得
,解得或
或
(2),
,解得
(3)由已知,
又,
,
解得
21.(2023·江西南昌·)(12分)已知直棱柱的底面ABCD为菱形,且,,点为的中点.
(1)证明:平面;
(2)求三棱锥的体积.
【答案】(1)证明见解析
(2)1
【解析】(1)连接AC交BD于点,连接,
在直四棱柱中,,
所以四边形为平行四边形,即,,
又因为底面ABCD为菱形,所以点为AC的中点,
点为的中点,即点为的中点,所以,,
即四边形为平行四边形,所以,
因为平面,平面,,所以平面;
(2)在直棱柱中平面,平面,
所以,
又因为上底面为菱形,所以,
因为平面,
所以平面,
因为在中,,
且点为BD的中点,所以,即,
所以.
22.(2023·云南昆明)如图①:在△ABC中,AB=BC=5,∠ABC=90°,DE∥BC,DE=2,将△ADE沿DE折起到△PDE的位置(如图②),且∠PEB=60°.
(1)请作出平面PBC与平面PDE的交线l(不需要说明理由)
(2)证明;平面PBC⊥平面PBE;
(3)求直线PE与平面PBC所成角的正弦值.
【答案】(1)答案见解析
(2)证明见解析
(3)
【解析】(1)因为,平面,平面,
所以平面,且平面,平面平面,
所以,
则过点作直线,使;
(2)因为,,且,
所以,且,且平面,平面,
所以平面,且平面,
所以平面平面;
(3)由(2)可知平面平面,
且平面平面,
所以直线在平面内的射影就是,则直线PE与平面PBC所成角为或其补角,
因为是等腰直角三角形,且,
所以也是等腰直角三角形,,,,
种,根据余弦定理,,
则,所以,
,
则,
所以直线PE与平面PBC所成角的正弦值为.
高中数学人教A版 (2019)必修 第二册第九章 统计9.1 随机抽样课后测评: 这是一份高中数学人教A版 (2019)必修 第二册<a href="/sx/tb_c4000309_t7/?tag_id=28" target="_blank">第九章 统计9.1 随机抽样课后测评</a>,共11页。试卷主要包含了抽样调查等内容,欢迎下载使用。
人教A版 (2019)必修 第二册7.1 复数的概念课后练习题: 这是一份人教A版 (2019)必修 第二册<a href="/sx/tb_c4000296_t7/?tag_id=28" target="_blank">7.1 复数的概念课后练习题</a>,共9页。试卷主要包含了复数,复数集,)))),公式,1 复数的概念,故选等内容,欢迎下载使用。
人教A版 (2019)必修 第二册9.1 随机抽样一课一练: 这是一份人教A版 (2019)必修 第二册<a href="/sx/tb_c4000309_t7/?tag_id=28" target="_blank">9.1 随机抽样一课一练</a>,共18页。试卷主要包含了4,2,1 随机抽样,4cm见解析等内容,欢迎下载使用。












