高三数学一轮复习第七章立体几何与空间向量第七课时向量法求距离及立体几何中的探索性、翻折问题课件

这是一份高三数学一轮复习第七章立体几何与空间向量第七课时向量法求距离及立体几何中的探索性、翻折问题课件，共37页。

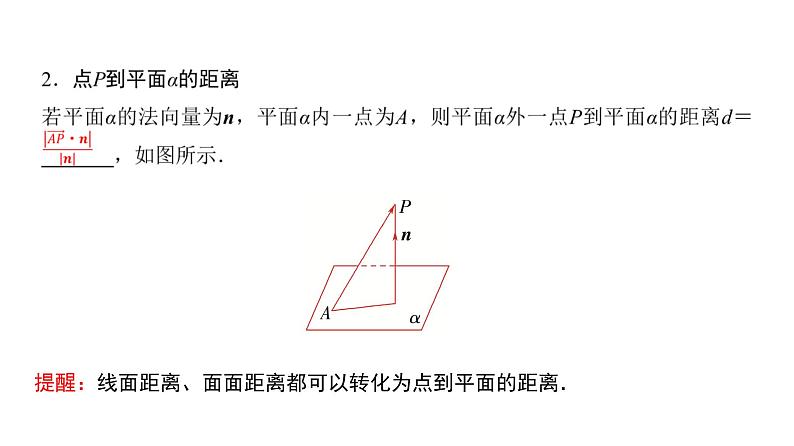
提醒：线面距离、面面距离都可以转化为点到平面的距离．
考向1　点到直线的距离[典例1]　(2024·济宁一中月考)如图，P为矩形ABCD所在平面外一点，PA⊥平面ABCD.若已知AB＝3，AD＝4，PA＝1，则点P到直线BD的距离为________．
考向2　点到平面的距离[典例2]　(2024·衡水中学月考)已知在长方体ABCD-A1B1C1D1中，AB＝6，BC＝4，BB1＝3，求点B1到平面A1BC1的距离．
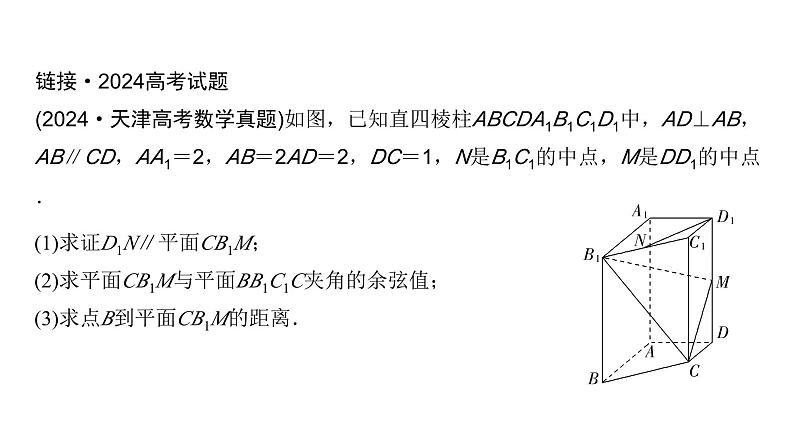
链接·2024高考试题(2024·天津高考数学真题)如图，已知直四棱柱ABCDA1B1C1D1中，AD⊥AB，AB∥CD，AA1＝2，AB＝2AD＝2，DC＝1，N是B1C1的中点，M是DD1的中点．
(1)求证D1N∥平面CB1M；(2)求平面CB1M与平面BB1C1C夹角的余弦值；(3)求点B到平面CB1M的距离．
(2)由题意知，AA1，AB，AD两两垂直，以A为原点建立如图所示空间直角坐标系，
点拨　用向量方法研究空间距离问题的一般步骤：(1)确定法向量；(2)选择参考向量；(3)利用公式求解．
跟进训练1　(2024·合肥模拟)如图，在正三棱柱ABC-A1B1C1中，各棱长均为4，N是CC1的中点．(1)求点N到直线AB的距离；(2)求点C1到平面ABN的距离．
[解]　(1)证明：∵四边形ABCD为正方形，则BC⊥AB，CD⊥AD，∵PB⊥BC，BC⊥AB，PB∩AB＝B，∴BC⊥平面PAB，∵PA⊂平面PAB，∴PA⊥BC.∵PD⊥CD，CD⊥AD，PD∩AD＝D，∴CD⊥平面PAD，∵PA⊂平面PAD，∴PA⊥CD，∵BC∩CD＝C，∴PA⊥平面ABCD.
点拨　(1)对于存在判断型问题的求解，应先假设存在，把“是否存在”问题转化为“点的坐标是否有解，是否有规定范围内的解”等．(2)对于位置探究型问题，通常借助向量，引进参数，综合已知和结论列出等式，解出参数．
考点三　立体几何中的翻折问题[典例4]　(2024·山东临沂质检)如图，四边形ABCD为正方形，E，F分别为AD，BC的中点，以DF为折痕把△DFC折起，使点C到达点P的位置，且PF⊥BF.(1)证明：平面PEF⊥平面ABFD；(2)求DP与平面ABFD所成角的正弦值．
[解]　(1)证明：由已知可得BF⊥PF，BF⊥EF，PF∩EF＝F，PF，EF⊂平面PEF，所以BF⊥平面PEF.又BF⊂平面ABFD，所以平面PEF⊥平面ABFD.
(1)证明：EF⊥PD；(2)求平面PCD与平面PBF所成的二面角的正弦值．
点拨　平面图形的翻折问题，关键是搞清翻折前后图形中线线关系、线面位置关系和度量关系的变化情况. 一般地，翻折后还在同一个平面上的相关关系不发生变化，不在同一个平面上的发生变化．
跟进训练3　(2024·陕西西安模拟)如图，菱形ABCD中，∠ABC＝60°，E为CD中点，将△ADE沿AE折起使得平面ADE⊥平面ABCE，BE与AC相交于点O，H是棱DE上的一点且满足DH＝2HE. (1)求证：OH∥平面BCD；(2)求平面ABC与平面BCD夹角的余弦值.
[解]　(1)证明：由题意知CE∥AB，AB＝2CE，所以OE∶OB＝1∶2. 又DH＝2HE，所以OH∥BD，又BD⊂平面BCD，OH⊄平面BCD，所以OH∥平面BCD.