






适用于新高考新教材备战2025届高考数学一轮总复习第8章立体几何与空间向量课时规范练58翻折问题与探索性问题课件新人教A版
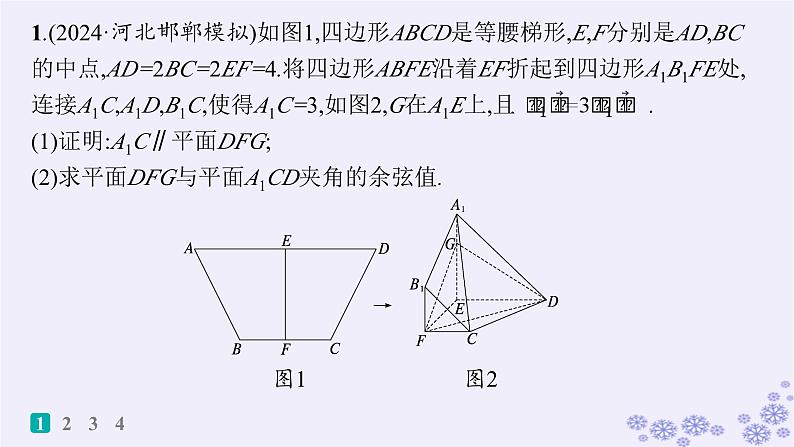
展开1.(2024·河北邯郸模拟)如图1,四边形ABCD是等腰梯形,E,F分别是AD,BC的中点,AD=2BC=2EF=4.将四边形ABFE沿着EF折起到四边形A1B1FE处,连接A1C,A1D,B1C,使得A1C=3,如图2,G在A1E上,且 .(1)证明:A1C∥平面DFG;(2)求平面DFG与平面A1CD夹角的余弦值.
图1 图2
(1)证明 连接CE,交DF于点H,连接GH.易证△CHF∽△EHD,
因为GH⊂平面DFG,A1C⊄平面DFG,所以A1C∥平面DFG.
(2)解 由题图1可知A1E⊥EF,DE⊥EF.因为AD=2BC=2EF=4,E,F分别是AD,BC的中点,所以CF=1,EF=A1E=2,则CE= 因为A1C=3,所以CE2+A1E2=A1C2,所以A1E⊥CE.因为EF,CE⊂平面CDEF,且EF∩CE=E,所以A1E⊥平面CDEF,所以A1E⊥ED,
又ED⊥EF,故以E为坐标原点,分别以直线EF,ED,EA1为x轴,y轴,z轴,建立如图所示的空间直角坐标系.
2.(2024·山东烟台模拟)如图,圆柱的轴截面ABCD是边长为6的正方形,下底面圆的一条弦EF交CD于点G,其中DG=2,DE=DF.(1)证明:平面AEF⊥平面ABCD.(2)判断上底面圆周上是否存在点P,使得二面角P-EF-A的余弦值为 ?若存在,求AP的长;若不存在,请说明理由.
(1)证明 由题意可知在下底面圆中,CD为直径.因为DE=DF,所以G为弦EF的中点,且EF⊥CD.因为EF⊥AD,AD∩CD=D,AD,CD⊂平面ABCD,所以EF⊥平面ABCD.因为EF⊂平面AEF,所以平面AEF⊥平面ABCD.
(2)解 设平面PEF交圆柱上底面于PQ,因为圆柱的上、下底面平行,所以平面PEF与上、下底面的交线平行,即EF∥PQ.设PQ交AB于点H.则二面角P-EF-A的大小就是二面角H-EF-A的大小.
分别以下底面垂直于DC的直线,直线DC,直线DA为x轴,y轴,z轴建立空间直角坐标系,如图所示.
3.(2024·山东青岛模拟)如图1,在矩形ABCD中,AB=4,AD=2,E为CD的中点,现将△ADE,△BCE分别沿AE,BE向上翻折,使点D,C分别到达点M,N的位置,且平面AME,平面BNE均与平面ABE垂直(如图2).(1)证明:M,N,A,B四点共面;(2)求直线AE与平面ABNM所成角的正弦值.
(1)证明 分别取AE,BE的中点F,G,连接MF,NG,FG.因为MA=ME,所以MF⊥AE.因为平面AME⊥平面ABE,平面AME∩平面ABE=AE,MF⊂平面AME,所以MF⊥平面ABE.同理可得NG⊥平面ABE,所以MF∥NG.在Rt△MAE中,MA=ME=2,
所以四边形MFGN是平行四边形,所以MN∥FG.因为F,G分别是AE,BE的中点,所以FG∥AB,所以MN∥AB,所以M,N,A,B四点共面.
(2)解 在题图1中,∠AED=∠BEC=45°,所以∠AEB=90°,所以AE⊥EB.取AB的中点H,连接FH,则FH∥BE,所以FA⊥FH.由(1)知直线FA,FH,FM两两垂直,以F为坐标原点,分别以直线FA,FH,FM为x轴,y轴,z轴,建立如图所示的空间直角坐标系,则F(0,0,0),
4.(2024·福建泉州模拟)如图,在三棱台ABC-A1B1C1中,AB=BC=2B1C1=2,D是AC的中点,E是棱BC上的动点.(1)试确定点E的位置,使AB1∥平面DEC1;(2)已知AB⊥BC1,CC1⊥平面ABC,设直线BC1与平面DEC1所成的角为θ,试在(1)的条件下,求cs θ的最小值.
解 (1)连接DC1,DE.因为AB=BC=2B1C1=2,D是AC的中点,所以A1C1∥AD,A1C1=AD,所以四边形ADC1A1为平行四边形,故AA1∥DC1.因为AA1⊄平面DEC1,DC1⊂平面DEC1,所以AA1∥平面DEC1.又AB1∥平面DEC1,且AB1,AA1⊂平面ABB1A1,AB1∩AA1=A,所以平面ABB1A1∥平面DEC1,又平面ABB1A1∩平面ABC=AB,平面ABC∩平面DEC1=DE,故DE∥AB,因为D是AC的中点,所以E是BC的中点,故点E在边BC的中点处,AB1∥平面DEC1.
(2)因为CC1⊥平面ABC,AB⊂平面ABC,所以CC1⊥AB,又AB⊥BC1,CC1∩BC1=C1,CC1,BC1⊂平面BCC1B1,故AB⊥平面BCC1B1,由于BC⊂平面BCC1B1,所以AB⊥BC.由(1)知E是BC的中点,D是AC的中点,所以ED∥AB,进而DE⊥BC.连接B1E,由B1C1∥EC,B1C1=EC,所以四边形B1C1CE为平行四边形,故CC1∥B1E,由于CC1⊥平面ABC,因此B1E⊥平面ABC,所以B1E⊥BC,B1E⊥ED,
又ED⊥BC,所以ED,EC,EB1两两垂直,以E为坐标原点,以直线EC,ED,EB1分别为x轴,y轴,z轴建立如图所示的空间直角坐标系.设B1E=a,则E(0,0,0),B(-1,0,0),C(1,0,0),D(0,1,0),C1(1,0,a),B1(0,0,a),
适用于新高考新教材备战2025届高考数学一轮总复习第8章立体几何与空间向量课时规范练55空间向量及其运算课件新人教A版: 这是一份适用于新高考新教材备战2025届高考数学一轮总复习第8章立体几何与空间向量课时规范练55空间向量及其运算课件新人教A版,共19页。PPT课件主要包含了ACD等内容,欢迎下载使用。
适用于新高考新教材备战2025届高考数学一轮总复习第8章立体几何与空间向量课时规范练53空间直线平面的垂直课件新人教A版: 这是一份适用于新高考新教材备战2025届高考数学一轮总复习第8章立体几何与空间向量课时规范练53空间直线平面的垂直课件新人教A版,共23页。PPT课件主要包含了A1C1⊥B1D1,ABD等内容,欢迎下载使用。
适用于新高考新教材备战2025届高考数学一轮总复习第8章立体几何与空间向量课时规范练52空间直线平面的平行课件新人教A版: 这是一份适用于新高考新教材备战2025届高考数学一轮总复习第8章立体几何与空间向量课时规范练52空间直线平面的平行课件新人教A版,共19页。PPT课件主要包含了BCD等内容,欢迎下载使用。












