高考数学一轮复习全程复习构想·数学（理）【统考版】第二节　一元二次不等式及其解法（课件）

展开

这是一份高考数学一轮复习全程复习构想·数学（理）【统考版】第二节　一元二次不等式及其解法（课件），共37页。PPT课件主要包含了必备知识基础落实，关键能力考点突破，微专题，答案D，－14，－53，答案A，答案C，答案B等内容，欢迎下载使用。

·最新考纲·1．会从实际情境中抽象出一元二次不等式模型．2．通过函数图象了解一元二次不等式与相应的二次函数、一元二次方程的联系．3．会解一元二次不等式，对给定的一元二次不等式，会设计求解的程序框图．
·考向预测·考情分析：不等式解法是不等式中的重要内容，且常考常新，“三个二次”之间的联系的综合应用等问题是高考考查的热点，题型多以选择题、填空题为主，难度中等偏下．学科素养：通过一元二次不等式及恒成立问题的求解考查数学运算、逻辑推理的核心素养．
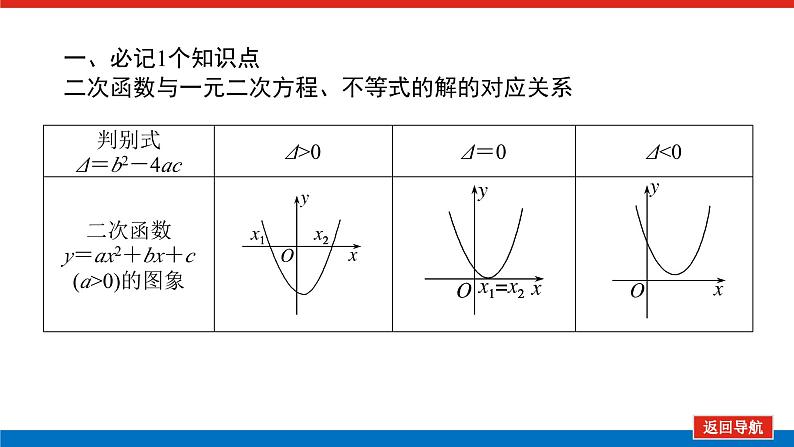
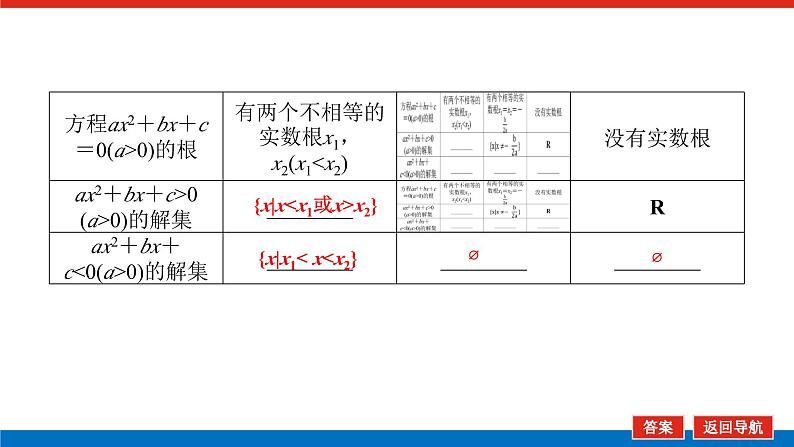
一、必记1个知识点二次函数与一元二次方程、不等式的解的对应关系
{x|xx2}
{x|x1< x(三)易错易混4．(不等式变形必须等价)不等式x(x＋5)<3(x＋5)的解集为________．
解析：原不等式等价于(x＋5)(x－3)<0，解得－55．(注意二次项系数的符号)不等式(x＋1)(3－2x)≥0的解集为_____________．
反思感悟　解一元二次不等式的4个步骤
考点二　含参数的一元二次不等式的解法　[综合性][例1]　解关于x的不等式ax2－(a＋1)x＋1<0(a>0)．
反思感悟　含参数的一元二次不等式求解步骤(1)讨论二次项系数的符号，即相应二次函数图象的开口方向．(2)讨论判别式的符号，即相应二次函数图象与x轴交点的个数．(3)当Δ>0时，讨论相应一元二次方程两根的大小．(4)最后按照系数中的参数取值范围，写出一元二次不等式的解集．
{x|x≥3或x≤2}
2．解不等式12x2－ax>a2(a∈R)．
考点三　一元二次不等式恒成立问题　[综合性]角度1　在R上的恒成立问题[例2]　对于任意实数x，不等式(a－2)x2－2(a－2)x－4<0恒成立，则实数a的取值范围是(　　)A．(－∞，2)　 B．(－∞，2]C．(－2，2) D．(－2，2]
反思感悟　一元二次不等式在R上恒成立的条件
角度2　在给定区间上的恒成立问题[例3]　已知函数f(x)＝mx2－mx－1.若对于x∈[1，3]，f(x)<5－m恒成立，则实数m的取值范围为___________．
角度3　给定参数范围的恒成立问题[例4]　若mx2－mx－1<0对于m∈[1，2]恒成立，则实数x的取值范围为___________．
反思感悟　给定参数范围求x范围的恒成立问题的解法解决恒成立问题一定要清楚选谁为主元，谁是参数．一般情况下，知道谁的范围，就选谁当主元，求谁的范围，谁就是参数．即把变元与参数交换位置，构造以参数为变量的函数，根据原变量的取值范围列式求解．
2．当x∈(1，2)时，不等式x2＋mx＋4<0恒成立，则m的取值范围是(　　)A.(－∞，4] B．(－∞，－5)C.(－∞，－5] D．(－5，－4)
微专题26 转化与化归思想在不等式中的应用
转化与化归思想，就是在研究和解决数学问题时采用某种方式，借助某种函数性质、图象、公式或已知条件将问题通过变换加以转化，进而达到解决问题的思想．
名师点评　(1)本题的解法充分体现了转化与化归思想；函数的值域和不等式的解集转化为a，b满足的条件；不等式恒成立可以分离常数，转化为函数值域问题．(2)注意函数f(x)的值域为[0，＋∞)与f(x)≥0的区别．
[变式训练]　已知函数f(x)＝x2＋ax＋b(a，b∈R)的值域为[0，＋∞)，若关于x的不等式f(x)

相关课件更多