数学七年级上册2 平行线的判定优秀ppt课件

这是一份数学七年级上册2 平行线的判定优秀ppt课件，共19页。PPT课件主要包含了教学目标，复习旧知，新知探究，平行线的判定，针对练习，课堂练习，BCD，ABC，课堂小结等内容，欢迎下载使用。

【教学目标】1．让学生理解并掌握平行线的四种判定方法； 2．让学生学会利用平行线的判定方法进行简单的推理；3．培养学生严密的逻辑思维能力和推理能力．【重点】平行线的判定．【难点】平行线判定的应用．
回顾以学的知识思考以下问题(1)怎样的两条直线平行？(2)过点P做 a∥b 你想到了什么？
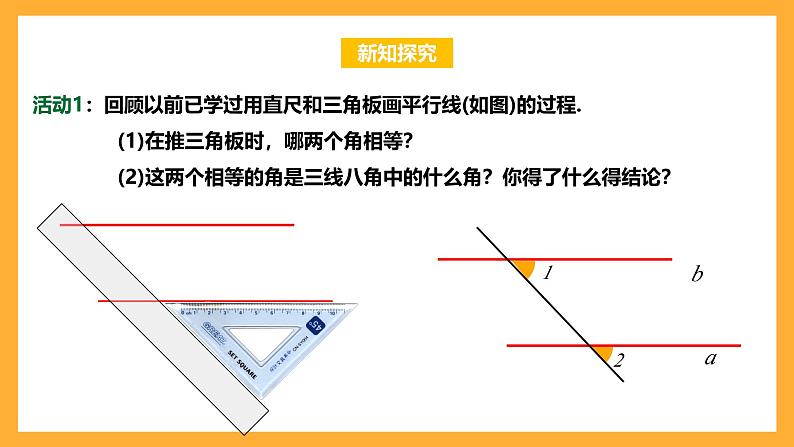
活动1：回顾以前已学过用直尺和三角板画平行线(如图)的过程.(1)在推三角板时，哪两个角相等？(2)这两个相等的角是三线八角中的什么角？你得了什么得结论？
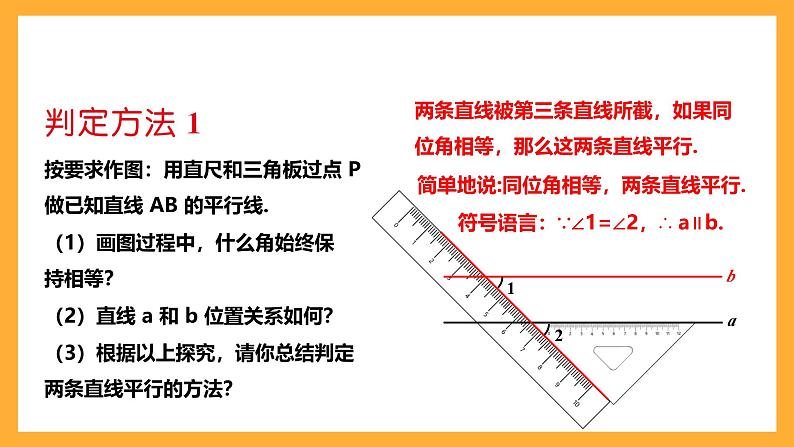
按要求作图：用直尺和三角板过点 P 做已知直线 AB 的平行线.
（1）画图过程中，什么角始终保持相等？
（2）直线 a 和 b 位置关系如何？
（3）根据以上探究，请你总结判定两条直线平行的方法？
两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行.
简单地说:同位角相等，两条直线平行.
符号语言：∵∠1=∠2，∴ a∥b.
如图，如果∠2=∠3，能得出 a∥b 吗？
你能用文字语言概括上面的结论吗？
∵∠2=∠3，∠1=∠3（对顶角相等）∴∠1=∠2.∴a∥b.（同位角相等，两直线平行）
两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行.
简单地说：内错角相等，两直线平行.
符号语言：∵∠2=∠3， ∴a∥b.
如果∠2＋∠4＝180°，能得出 a∥b 吗？
∵ ∠4+∠2=180°，∠4+∠1=180°（已知）∴∠2=∠1 （同角的补角相等）∴a∥b. （同位角相等，两条直线平行）
两条直线被第三条直线所截，如果同旁内角互补，那么两条直线平行.
简单地说：同旁内角互补，两直线平行.
符号语言： ∵∠4+∠2=180°，∴ a∥b.
判定方法 1 同位角相等，两直线平行．判定方法 2 内错角相等，两直线平行．判定方法 3 同旁内角互补，两直线平行．
① ∵ ∠2 = ∠ 6（已知）∴ ___∥___ ( )
② ∵ ∠3 = ∠5（已知） ∴ ___∥___ ( )
③∵ ∠4 +___=180（已知） ∴___∥___ ( )
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
根据条件完成填空.
例1 如图,直线a、b被直线l所截,已知∠1=115°，∠2=115°，直线a、b平行吗?为什么?
分析：由已知条件可得∠1=∠2.根据内错角相等,两直线平行，可知a // b.”我们用符号“∵”‘’∴“分别表示“因为”“所以”.于是分析中的推理过程就可以写成如下形式.
解：∵∠1=115°，∠2=115°(已知)，∴∠1 =∠2(等量代换)，∴a//b(内错角相等,两直线平行).
括号内所写的,就是括号前这一结论成立的理由.等量代换以及等式的性 质是我们常用的推理依据.
例2 如图,在四边形ABCD中，已知∠B=60°,∠C=120°，AB与CD平行吗?AD与BC平行吗?
解∵∠B=60°，∠C=120°(已知) ,∴∠B+∠C=180°(等式的性质)∴AB // CD(同旁内角互补，两直线平行).本题中，根据已知条件，无法判定AD与BC是否平行.
例3 如图,直线CD、EF均与直线AB垂直，D、F为垂足.试判断CD与EF是否平行.
解∵CD⊥AB,EF⊥AB(已知)，∴∠ADC=∠AFE= 90°，∴CD // EF(同位角相等,两直线平行).此例告诉我们:
在同一平面内，垂直于同一条直线的两条直线平行.
1.如图,可以确定AB∥CE的条件是( )A.∠2=∠BB. ∠1=∠AC. ∠3=∠BD. ∠3=∠A
2.如图,已知∠1=30°,∠2或∠3满足条件________________ ____，则a//b.
∠2＝150°或 ∠3＝30°
3．如图，已知∠1＝∠2，则下列结论正确的是( )　A．AD∥BC B．AB∥CD　C．AD∥EF D．EF∥BC
4．如图，若∠1＝∠2，则DE∥AB；若∠2＝∠3，则BC∥_____．
5.如图.（1）从∠1=∠4，可以推出　 ∥ ， 理由是 .
(2)从∠ABC +∠ =180°，可以推出AB∥CD ，理由是 .
内错角相等，两直线平行
(3)从∠ =∠ 2 ，可以推出AD∥BC，理由是______________________.
(4)从∠5=∠ ，可以推出AB∥CD，理由是__________________
6．如图，已知AB⊥AD，CD⊥AD，∠1＝∠2，那么直线AE，DF平行吗？为什么？
解：AE与DF平行．理由如下：∵AB⊥AD，CD⊥AD，∴∠BAD＝∠ADC＝90°.又∵∠1＝∠2，∴∠BAD－∠1＝∠ADC－∠2，即∠DAE＝∠ADF，∴AE∥DF.
判定方法1：两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行．简单地说，就是同位角相等，两直线平行
判定方法2：两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行．简单地说，就是内错角相等，两直线平行
判定方法3：两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行．简单地说，就是同旁内角互补，两直线平行