上教版 (2020)必修第三册2 茎叶图优质课件ppt

这是一份上教版 (2020)必修第三册2 茎叶图优质课件ppt，共20页。

频率分布直方图并不是展示数据分布的唯一选择 ． 在数据不多的情况下 ， 我们可以绘制 茎叶图 （ ｓｔｅｍａｎｄｌｅａｆｐｌｏｔ ）， 展示所有样本数据的信息
例如 ， 某个品种的小麦麦穗长度 （ 单位 ： ｃｍ ） 的样本数据如下所示 ， 如何分析该品种小麦的麦穗长度的分布情况呢？
１０． ２，９． ７，７． ８，１０． ０， ９． １， ８． ９， ８． ６，９． ８， ９． ６，９． ７，１１． ２，１０． ６，１１． ７
解读茎叶图和解读直方图一样 ， 要注意整体形态 ． 从这张图可以直观地看出该品种的麦穗的长度主要集中在 ９～１０ｃｍ 之间 ，并且分布比较对称 ．茎叶图既可以用于呈现单组数据 ， 也可以用于对两组同类数据的比较分析 ．
在上述问题中 ， 我们将样本数据分为茎和叶两个部分 ： 整数部分作为 “ 茎 ”， 小数作为 “ 叶 ” ． 对于第一个麦穗长度数据 １０． ２ 来说 ， １０ 是茎 ， ２ 则是叶 ． 然后把 “ 茎 ” 由小到大 、 从上往下写成一列 ， 并在其左边或右边画一条竖直的线 （ 不妨画在右边 ） ． 最后把“ 叶 ” 写在它所属的 “ 茎 ” 的右边 ， 由小到大排成一行 ． 这样就得到该品种麦穗长度的茎叶图 （ 图 １３-４-３ ）
例1. 根据表 １３-２ 中的数据 ， 分别绘制女生和男生的体重分布茎叶图 ， 并比较女生和男生的体重分布 ．
解 　 因为表 １３-２ 中的数据不是很多 ， 而且学生的体重都是两位数 ， 所以可以比较方便地绘制茎叶图 ． 我们把表示体重的两位数的十位数字作为 “ 茎 ”， 从小到大排列在中间 ， 男女生体重的个位数字作为 “ 叶 ” 分列在两边 ， 以便于比较 ， 就得到下面的茎叶图 （ 图 １３-４-４ ）：
从图中可以看出 ， 女生的体重整体上低于男生的体重 ． 此外 ， 女生的体重分布集中程度较高 ， 男生的体重分布相对分散一些 ．
用茎叶图展示数据的优点在于所有信息都可以从茎叶图中得到 ， 由茎叶图也很容易制作相应的频率分布表和频率分布直方图
在图 １３-４-４ 中 ，“ 茎 ” 为 ４ 的男生有体重为 ４７ｋｇ 和 ４８ｋｇ 两位 “ 叶 ” 中就有 ７ 、 ８ 两个数字 ， 其余类同 ．
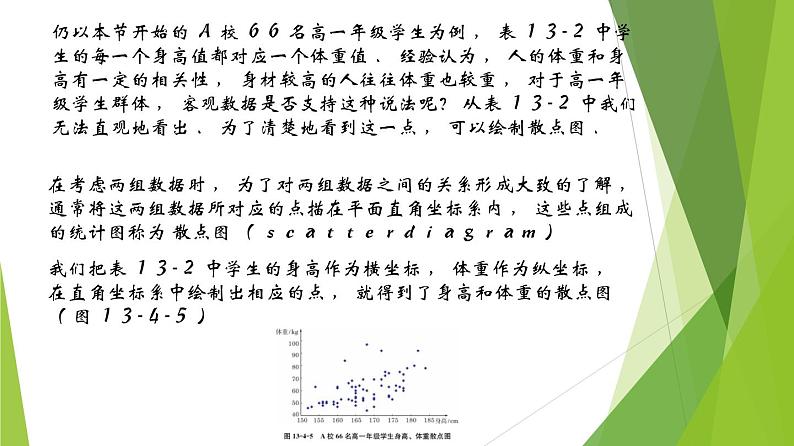
仍以本节开始的 Ａ 校 ６６ 名高一年级学生为例 ， 表 １３-２ 中学生的每一个身高值都对应一个体重值 ． 经验认为 ， 人的体重和身高有一定的相关性 ， 身材较高的人往往体重也较重 ， 对于高一年级学生群体 ， 客观数据是否支持这种说法呢？ 从表 １３-２ 中我们无法直观地看出 ． 为了清楚地看到这一点 ， 可以绘制散点图 ．
在考虑两组数据时 ， 为了对两组数据之间的关系形成大致的了解 ， 通常将这两组数据所对应的点描在平面直角坐标系内 ， 这些点组成的统计图称为 散点图 （ ｓｃａｔｔｅｒｄｉａｇｒａｍ ）
我们把表 １３-２ 中学生的身高作为横坐标 ， 体重作为纵坐标 ，在直角坐标系中绘制出相应的点 ， 就得到了身高和体重的散点图（ 图 １３-４-５ ）
从图 １３-４-５ 中可以直观地看出 ， 图中的点从左至右大致是逐渐上升的 ， 也就是说 ，“ 身材较高的人 ， 体重往往也较重 ” 这一说法在高一年级学生群体中就总体而言是对的
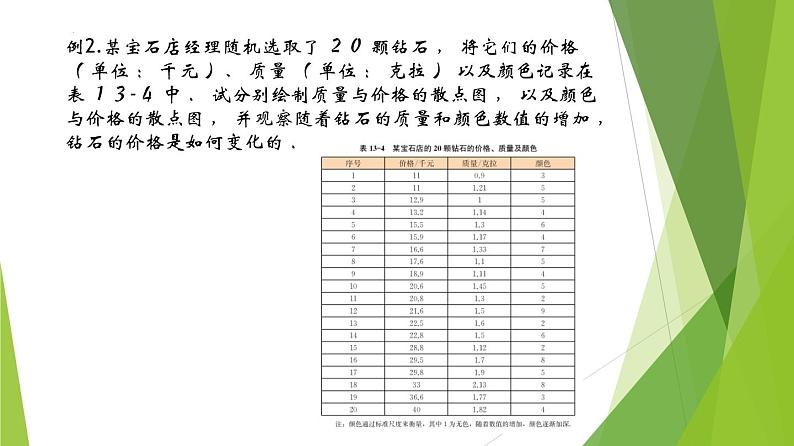
例2.某宝石店经理随机选取了 ２０ 颗钻石 ， 将它们的价格（ 单位 ： 千元 ）、 质量 （ 单位 ： 克拉 ） 以及颜色记录在表 １３-４ 中 ． 试分别绘制质量与价格的散点图 ， 以及颜色与价格的散点图 ， 并观察随着钻石的质量和颜色数值的增加 ， 钻石的价格是如何变化的 ．
解 　 我们将价格作为纵坐标 ， 质量和颜色分别作为横坐标 ，分别绘制散点图 ， 如图 １３-４-６ 所示
从图 １３-４-６ 中我们可以看出 ， 随着钻石质量的增加 ， 钻石的价格呈现逐渐上升的趋势 ， 但价格的增减随着颜色的变化却看不出明显的规律 ， 这说明价格和颜色之间可能不存在明显的关系
我们在这一节讨论了频率分布直方图 、 茎叶图以及散点图 ．在初中阶段我们还学习了条形图 、 扇形图以及折线图等 ． 在对数据进行分析和整理时 ， 应根据需要选择恰当的统图 ． 散点图一般用于刻画成对的数据 ， 并且可以从图中看出成对数据之间是否存在某种关系 ． 茎叶图呈现了数据的所有信息 ， 但不适合数据量较大的情形 ． 当数据量较大时一般选用条形图或频率分布直方图 ， 它们能直观地反映数据分布的大致况 ． 而如果想呈现每部分所占的比例 ， 则需要用到扇形图 ． 折线图则主要用于呈现数据随着时间变化的趋势
操作 ： 调查本校学生户外活动时间与视力
调查你校本年级学生的每天平均户外活动时间和视力情况 ，并用合适的统计图表呈现出来 ． 你能发现这两者之间有什么关系吗？
信息技术 ： 绘制统计图表
运用计算机中的电子表格办公软件可以绘制多种统计图表 ．尽管不同版本的处理细节略有不同 ， 但基本过程类似 ． 严格来说 ， 它们并不是统计软件 ， 但作为办公软件 ， 具有一定的统计计算功能 ， 并且可以实施简单的数据统计 、 图表绘制等操作 ． 要做更复杂 、 更专业的统计工作 ， 软件市场上有比较成熟的统计分析软件 ， 可供选用
（ ２ ） 选中这两列或两行数据 ， 在 “ 插入 ” 菜单中选择所需要的图像类型 ——— 散点图 ； 根据需要选择其中一种散点图的类型并单击 （ 图 １３－４－７ ）， 一幅散点图即出现在工作簿中
下面以表 １３２ 的数据为例 ， 绘制散点图 ．（ １ ） 在工作簿中输入身高和对应体重的两列或两行数据
（ ３ ） 根据需要选择坐标轴的范围以及单位长度等 ， 使得统计图具有较好的可视性 ． 例如 ， 横坐标身高的范围可以取［ １５０ ， １８５ ） ， 纵坐标体重的范围可以取 ［ ４０ ， １００ ） ， 修改后就得到了图 １３－４－５．
１． 下表是某沿海地区的气温和海水表层温度 （ 单位 ： ℃ ） 的统计数据 ， 根据下表绘制茎叶图 ， 并比较气温与海水表层温度的分布情况
２． 下列关于散点图的说法中 ， 正确的是 （ 　　 ）Ａ． 任意给定统计数据 ， 都可以绘制散点图 ；Ｂ． 从散点图中可以看出两个量是否具有一定的关系 ；Ｃ． 从散点图中可以看出两个量的因果关系 ；Ｄ． 从散点图中无法看出数据的分布情况 ．３． 某研究人员随机抽取 １５ 棵某品种的栎树 ， 测得树高 （ 单位 ： ｍ ） 和胸径 （ 指地面以上１． ３ｍ 处树干的直径 ， 单位 ： ｃｍ ） 的数据 ， 如下表所示 ．
绘制散点图 ， 并观察随着高度的增加 ， 栎树胸径的变化趋势 ．
1、如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位：分)．已知甲组数据的中位数为15，乙组数据的平均数为16.8，则x，y的值分别为(　　)A．2，5 B．5，5 C．5，8 D．8，8
【答案】C；【解析】由于甲组数据的中位数为15＝10＋x，所以x＝5，
2、在如图所示的茎叶图中，甲、乙两组数据的中位数分别是____________，____________．
【答案】45；46；【解析】甲组数据为：28，31，39，42，45，55，57，58，66，中位数为45.乙组数据为：29，34，35，42，46，48，53，55，67，中位数为46.
3、某市场去年各月份的收入、支出的统计数据如图所示，已知利润＝收入－支出，请根据此统计图写出一个关于利润的正确统计结论：_______________________________________________________________________________________________________________________.
【解析】由题图可得，1月到12月的利润分别为20万元，20万元，30万元，20万元，20万元，20万元，20万元，10万元，20万元，30万元，20万元，20万元．【答案】去年各月份利润的最小值为10万元(答案不唯一，也可以是：去年各月份利润的最大值为30万元，全年总利润为250万元，去年月平均利润约为20.8万元，去年各月份利润众数为20万元等)；