专题17 同角三角函数的基本关系和诱导公式5题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测（原卷版）

这是一份专题17 同角三角函数的基本关系和诱导公式5题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测（原卷版），共13页。试卷主要包含了同角三角函数基本关系，三角函数诱导公式，填空题，解答题等内容，欢迎下载使用。


一、同角三角函数基本关系
1、同角三角函数的基本关系
（1）平方关系：．
（2）商数关系：；
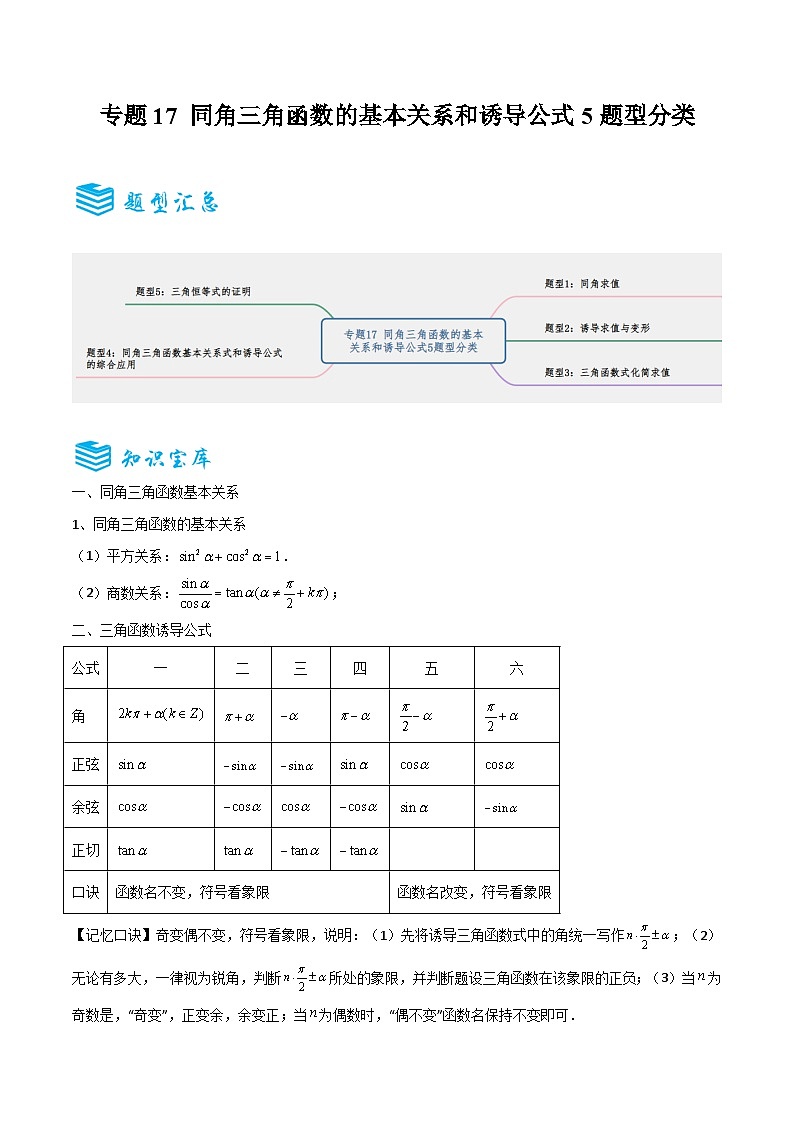
二、三角函数诱导公式
【记忆口诀】奇变偶不变，符号看象限，说明：（1）先将诱导三角函数式中的角统一写作；（2）无论有多大，一律视为锐角，判断所处的象限，并判断题设三角函数在该象限的正负；（3）当为奇数是，“奇变”，正变余，余变正；当为偶数时，“偶不变”函数名保持不变即可．
注：1、利用可以实现角的正弦、余弦的互化，利用可以实现角的弦切互化．
2、“”方程思想知一求二．
一、单选题
1．（2024·全国·模拟预测）已知，则（ ）
A．B．C．D．
2．（2024·四川巴中·模拟预测）勾股定理，在我国又称为“商高定理”，最早的证明是由东汉末期数学家赵爽在为《周髀算经》作注时给出的，他利用了勾股圆方图，此图被称为“赵爽弦图”.“赵爽弦图”是由四个全等的直角三角形和中间的一个小正方形组成的大正方形图案（如图所示），若在大正方形内随机取一点，该点落在小正方形内的概率为，则“赵爽弦图”里的直角三角形中最小角的正弦值为（ ）

A．B．C．D．
3．（2024·全国·模拟预测）已知，则（ ）
A．B．2C．D．
4．（2024·山西·模拟预测）已知为锐角，且，则（ ）
A．B．C．D．
5．（2024高三上·安徽合肥·阶段练习）已知角为钝角，且角终边上有一点，则角（ ）
A．B．C．D．
6．（2024高三上·宁夏银川·阶段练习）在平面直角坐标系中，在在角终边上，则的值为（ ）
A．B．C．D．
7．（2024高三上·四川成都·期中）已知角的顶点与坐标原点重合，始边与x轴的正半轴重合，若角的终边与角的终边相同，则( )
A．B．C．D．
8．（2024·全国·模拟预测）已知直线的倾斜角为，则（ ）
A．B．C．D．
9．（2024·陕西宝鸡·一模）已知，则（ ）
A．B．C．D．
10．（2024·全国·模拟预测）已知，则（ ）
A．B．C．D．
11．（2024·全国·模拟预测）已知圆，过点，作圆的两条切线，切点分别为，则（ ）
A．B．C．D．
12．（2024·河南郑州·模拟预测）已知，则（ ）
A．B．C．D．
13．（2024·陕西西安·二模）已知，则（ ）
A．B．C．-D．
14．（2024·广东深圳·模拟预测）已知，则的值为（ ）
A．B．C．D．
15．（2024高三上·陕西西安·阶段练习）若，则的值为（ ）
A．B．C．D．
16．（2024高三上·陕西西安·阶段练习）若，则的值为（ ）
A．B．C．D．
17．（2024·贵州贵阳·模拟预测）已知，则（ ）
A．B．C．D．
18．（2024高一下·湖南长沙·阶段练习）已知，且，（ ）
A．B．C．D．
19．（2024高三下·重庆渝中·阶段练习）已知是三角形的一个内角，且满足，则（ ）
A．2B．1C．3D．
20．（2024高三上·北京·阶段练习）在平面直角坐标系中，角与角均以为始边，它们的终边关于直线对称，若，则（ ）
A．B．C．D．
21．（2024·辽宁抚顺·模拟预测）已知，则“”是“”的（ ）
A．充要条件B．既不充分也不必要条件C．充分不必要条件D．必要不充分条件
22．（2024·陕西榆林·二模）已知，则=（ ）
A．B．C．D．
23．（2024高三上·北京海淀·阶段练习）已知为第二象限的角，且，则的值为（ ）
A．B．C．D．
24．（2024高一上·山西太原·阶段练习）已知，且，则（ ）
A．B．C．D．
25．（2024·全国·模拟预测）已知，则（ ）
A．B．C．D．
26．（2024高三上·云南昆明·阶段练习）若，，则（ ）
A．B．C．D．
27．（2024高三上·四川成都·阶段练习）已知角的终边过点，则的值是（ ）
A．B．C．D．
28．（2024高三上·安徽·阶段练习）在平面直角坐标系中，设角的顶点与原点重合，始边与轴的非负半轴重合，若角的终边过点，则（ ）
A．B．C．D．
29．（2024高三上·安徽·期中）已知是角的终边上一点，则（ ）
A．B．C．D．
30．（2024高三上·安徽·期中）已知角的顶点在坐标原点，始边与轴的非负半轴重合，终边经过点，则（ ）
A．B．C．0D．
31．（2024高一上·江苏常州·阶段练习）若 ，则（ ）
A．B．C．D．
32．（2024高三上·重庆永川·期中）已知，，则（ ）
A．B．C．3D．
33．（2024高一下·山东潍坊·阶段练习）下列化简正确的是（ ）
A．B．
C．D．
二、多选题
34．（2024·辽宁·模拟预测）设为第一象限角,,则（ ）
A．
B．
C．
D．
35．（江苏省宜兴中学、泰兴中学、泰州中学2023-2024学年高一上学期12月联合质量检测数学试卷）质点和在以坐标原点为圆心，半径为1的圆上逆时针作匀速圆周运动，同时出发.的角速度大小为，起点为圆与轴正半轴的交点，的角速度大小为，起点为角的终边与圆的交点，则当与重合时，的坐标可以为（ ）
A．B．
C．D．
36．（2024高一下·河南焦作·阶段练习）已知角，是锐角三角形的三个内角，下列结论一定成立的有（ ）
A．B．
C．D．
37．（2024高一下·河北沧州·阶段练习）在△ABC中，下列关系式恒成立的有（ ）
A．B．
C．D．
38．（2024高一上·江苏无锡·阶段练习）下列结论正确的有（ ）
A．B．
C．D．
39．（2024高一上·黑龙江齐齐哈尔·期末）已知下列等式的左右两边都有意义，则下列等式恒成立的是（ ）
A．B．
C．D．
三、填空题
40．（2024·全国）若，则 ．
41．（2024高一上·福建莆田·阶段练习）已知，，那么 .
42．（2024高三·全国·对口高考）若，求的值为 .
43．（2024高三上·江西南昌·阶段练习）若，则 .
44．（2024·上海浦东新·模拟预测）已知是关于的方程的两根，则 .
45．（2024高三·全国·专题练习）已知，则 ．
46．（2024高三上·安徽合肥·阶段练习）已知，，且为第二象限角，则 .
47．（2024·全国·模拟预测）若，则的最大值为 ，的最小值为 ．
48．（2024·四川绵阳·三模）已知，，则 .
49．（2024·山西阳泉·三模）已知，且，则 ．
50．（2024·浙江温州·二模）已知，则 .
51．（2024·黑龙江哈尔滨·二模）已知，则的值是 ．
52．（2024高三·全国·专题练习）已知，则 ．
53．（2024高三上·湖南衡阳·期中）已知，则 ．
54．（2024·全国·模拟预测）已知，则 .
55．（2024高三上·内蒙古包头·阶段练习）若，则 .
56．（2024高一下·黑龙江佳木斯·开学考试）已知，且，则 ．
57．（2024高一上·新疆乌鲁木齐·期末）已知角的终边与单位圆交于点，则 .
58．（2024高一·全国·课后作业）若角的终边落在直线上，则 ．
四、解答题
59．（2024高三·全国·专题练习）已知角的终边落在直线上．求
(1)的值；
(2)的值．
60．（2024高一下·安徽·期中）已知角的顶点为坐标原点，始边为轴的非负半轴，终边与单位圆相交于点P，若点位于轴上方且.
(1)求的值；
(2)求的值.
61．（2024高一上·广东东莞·阶段练习）如图，在平面直角坐标系中，为单位圆上一点，射线绕点O按逆时针方向旋转后交单位圆于点B，点B的横坐标为.
(1)求的表达式，并求；
(2)若，，求的值.
62．（2024高一·全国·课后作业）求证:.
63．（2024高二·全国·课后作业）证明：.
64．（2024高一上·四川广安·期末）已知
(1)化简；
(2)若是第三象限角，且，求的值.
65．（2024高一·全国·课后作业）证明：，．
66．（2024高一·全国·专题练习）求证：．
67．（2024高一上·全国·课后作业）（1）求证：；
（2）设，求证.
68．（2024高三·全国·对口高考）若，求的值.
69．（2024高三上·河南周口·期中）（1）若，求的值；
（2）设，求的值.
70．（2024高三上·江苏扬州·期末）在平面直角坐标系中，是坐标原点，角的终边与单位圆的交点坐标为，射线绕点按逆时针方向旋转弧度后交单位圆于点，点的纵坐标关于的函数为
(1)求函数的解析式，并求的值；
(2)若，，求的值
公式
一
二
三
四
五
六
角
正弦
余弦
正切
口诀
函数名不变，符号看象限
函数名改变，符号看象限
（一）
同角求值
（1）若已知角的象限条件，先确定所求三角函数的符号，再利用三角形三角函数定义求未知三角函数值．
（2）若无象限条件，一般“弦化切”．
题型1：同角求值
1-1．（2024高一上·广东江门·期末）已知 ，求 ，的值.
1-2．（2024高三·全国·专题练习）已知，则 .
1-3．（2024高三·全国·对口高考）已知，求值：
(1)；
(2)；
(3).
1-4．（2024高三上·黑龙江哈尔滨·阶段练习）已知，是关于的一元二次方程的两根．
(1)求的值；
(2)若，求的值．
1-5．（2024高三·山西运城·学业考试）已知，求下列各式的值：
(1)；
(2).
（二）
诱导求值与变形
（1）诱导公式用于角的变换，凡遇到与整数倍角的和差问题可用诱导公式，用诱导公式可以把任意角的三角函数化成锐角三角函数．
（2）通过等诱导变形把所给三角函数化成所需三角函数．
（3）等可利用诱导公式把的三角函数化
题型2：诱导求值与变形
2-1．（2024高三·全国·专题练习）的值为
2-2．（2024高一下·甘肃天水·期末）化简
2-3．（2024高三上·福建莆田·期中）已知则 ．
2-4．（2024高三·江苏·对口高考）已知，且，则的值是 .
2-5．（2024高三上·山东泰安·期中）已知是第四象限角，且，则 .
2-6．（2024高一上·湖南长沙·阶段练习）若、是关于的方程的两个根，则 .
2-7．（2024高三·全国·专题练习）（ ）
A．B．C．D．
（三）
同角三角函数基本关系式和诱导公式的综合应用
（1）利用同角三角函数关系式和诱导公式求值或化简时，关键是寻求条件、结论间的联系，灵活使用公式进行变形．
（2）注意角的范围对三角函数符号的影响．
题型3：三角函数式化简求值
3-1．（2024高三上·江苏淮安·阶段练习）已知为第二象限角，且满足，则
3-2．（2024·江苏苏州·模拟预测）已知，若，则= .
3-3．（2024高一上·天津和平·期末）已知角的终边经过点，则（ ）
A．B．C．D．1
3-4．（2024高三·全国·专题练习）已知sin(3π＋θ)＝，则＋＝ .
3-5．（2024高三上·江苏南通·阶段练习）已知，则（ ）
A．B．C．D．
题型4：同角三角函数基本关系式和诱导公式的综合应用
4-1．（2024高一上·江苏淮安·期末）已知，且．
(1)求的值；
(2)求的值．
4-2．（2024高一下·山东东营·期中）已知角满足
(1)若角是第三象限角，求的值;
(2)若，求的值.
4-3．（2024高三·全国·专题练习）已知，求的值．
4-4．（2024高一上·广东深圳·期末）已知．
(1)求的值．
(2)求的值．
（四）
三角恒等式的证明
三角恒等式的证明中涉及到同角三角函数基本关系，和角公式，差角公式，二角公式，辅助角公式等基本知识点，理解和掌握这些基本知识点是解答该类问题的基础和关键
题型5：三角恒等式的证明
5-1．（2024高一·全国·课后作业）求证：当或3时，.
5-2．（2024高一·全国·课前预习）求证：＝．
5-3．（2024高一·全国·课后作业）求证：
（1）；
（2）；
（3）；
（4）.
5-4．（2024高三·全国·专题练习）（1）求证：tan2αsin2α=tan2α-sin2α；
（2）已知tan2α=2tan2β+1，求证：2sin2α=sin2β+1.