






还剩20页未读,
继续阅读
所属成套资源:七年级数学冀教版(2024)上册课件
成套系列资料,整套一键下载
七年级数学冀教版(2024)上册课件 2.7 角的和与差
展开
这是一份七年级数学冀教版(2024)上册课件 2.7 角的和与差,共28页。
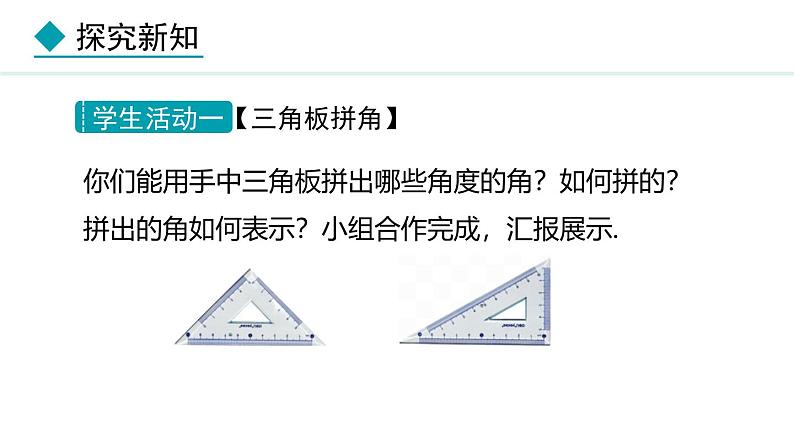
第二章 几何图形的初步认识 2.7 角的和与差1.结合具体图形,了解两个角的和与差的意义,会进行角的和差运算2.了解角平分线,通过折纸活动,进一步理解角平分线的意义.3.掌握余补角的定义,经历余、补角性质的探究过程,体会简单的推理.学习重点:角的和差运算,角平分线的意义, 互余、互补的概念与性质.学习难点:余、补角性质的理解与应用.线段可以比较长短,可以进行线段的和差运算;类似地,角可以比较大小,也可以进行角的和差运算,那么如何进行和差运算呢?你们能用手中三角板拼出哪些角度的角?如何拼的?拼出的角如何表示?小组合作完成,汇报展示.如图,在∠AOB的内部做射线OC,思考下列问题:(1)如图,图中都有哪些角?(2)这些角之间有怎样的关系?在∠AOB的内部做射线,有没有特殊的线?特殊的原因?角的平分线定义:从一个角的顶点引出的一条射线,把这个角分成两个相等的角,那么这条射线叫做这个角的平分线. 拿出半透明纸,在纸上画出一个角,你能不能折出这个角的平分线?(实际操作,并说一说你是怎样折的?)(1)在半透明纸上画出∠AOB.(2)折纸时,过顶点,使角的两边重合.(3)把纸展开,以O为端点,沿折痕画射线OP,如图所示.1.如果∠AOC=∠DOB ,那么∠AOD与 ∠COB相等吗?说明理由 .2.如图: 已知OP是∠AOC 的平分线 , OQ是 ∠COB的平分线。(1)已知∠POC=21 °,求∠AOC的度数。(2)已知∠BOC=40 °,求∠COQ的度数。(3)∠AOB=82 ° 请指明∠POQ的度数,并说明理由 如图,已知∠1=103°24′28" ,∠2= 30°54",求∠1+∠2 和∠1-∠2 的度数 .∠1+∠2 = 103°24′28" +30°54" .所以∠1+∠2 = 133°25′22" .(82" = 1′22" )解:∠1 - ∠2 = 103°24′28" +30°54" .所以∠1-∠2 = 73°23′ 34"(24′28"= 23′88")解: 解: ∠1+ ∠2=22°17′+∠2=90° ∠3+∠4=124°15′+55°45′=180°计算:(1)若∠1=22°17′ ,∠2=67°43′, 求∠1+ ∠2?(2)若∠3=124°15′ , ∠4=55°45′,求∠3+ ∠4?如果两个角的和等于90 °,那么就说这两个角互为余角,简称互余.其中一个角叫做另一个角的余角.如果两个角的和等于180 °,那么就说这两个角互为补角,简称互补.其中一个角叫做另一个角的补角.∵∠α+∠β=90° ∴∠α与∠β互为余角∵∠α+∠β=180°∴∠α与∠β互为补角数学语言:在图(1)中,∠AOB=90°;在图⑵中,∠DSE=180°.写出互为余角、互为补角的角。解:∠AOC与∠BOC互为余角,∠DSF与∠ESF互为补角.一起探究1.如果∠1和∠2都是∠α的余角,那么∠1和∠2相等吗?试着说说理由.2.如果∠3和∠4都是∠β的补角,那么∠3和∠4相等吗?试着说说理由.性质:同角(或等角)的余角相等,同角(或等角)的补角相等1.如图,已知∠1+∠3=90°,∠2+∠3=90°,∠1+∠4=90°,请写出∠1,∠2,∠3,∠4中的等量关系,并试着说说理由.解:∠1=∠2,∠3=∠4.理由:因为∠1+∠3=90°,∠2+∠3=90°,所以∠1=∠2.因为∠1+∠3=90°,∠1+∠4=90°,所以∠3=∠4(同角的余角相等).2.如图,直线AB与∠COD的两边OC,OD分别相交于点E,F,∠1+∠2=180°. 找出图中与∠2相等的角,并说明理由.解:因为∠1+∠3=180°,∠1+∠2=180°,所以∠3=∠2.因为∠1+∠4=180°,∠1+∠2=180°,所以∠4=∠2.因为∠2+∠5=180°,∠6+∠5=180°,所以∠2=∠6.所以图中与∠2相等的角有∠3,∠4,∠6.本节课探究了角哪些问题?在探究角的和差与相关性质时,你经历了什么?积累了哪些活动经验?完成课后习题+练习册.
第二章 几何图形的初步认识 2.7 角的和与差1.结合具体图形,了解两个角的和与差的意义,会进行角的和差运算2.了解角平分线,通过折纸活动,进一步理解角平分线的意义.3.掌握余补角的定义,经历余、补角性质的探究过程,体会简单的推理.学习重点:角的和差运算,角平分线的意义, 互余、互补的概念与性质.学习难点:余、补角性质的理解与应用.线段可以比较长短,可以进行线段的和差运算;类似地,角可以比较大小,也可以进行角的和差运算,那么如何进行和差运算呢?你们能用手中三角板拼出哪些角度的角?如何拼的?拼出的角如何表示?小组合作完成,汇报展示.如图,在∠AOB的内部做射线OC,思考下列问题:(1)如图,图中都有哪些角?(2)这些角之间有怎样的关系?在∠AOB的内部做射线,有没有特殊的线?特殊的原因?角的平分线定义:从一个角的顶点引出的一条射线,把这个角分成两个相等的角,那么这条射线叫做这个角的平分线. 拿出半透明纸,在纸上画出一个角,你能不能折出这个角的平分线?(实际操作,并说一说你是怎样折的?)(1)在半透明纸上画出∠AOB.(2)折纸时,过顶点,使角的两边重合.(3)把纸展开,以O为端点,沿折痕画射线OP,如图所示.1.如果∠AOC=∠DOB ,那么∠AOD与 ∠COB相等吗?说明理由 .2.如图: 已知OP是∠AOC 的平分线 , OQ是 ∠COB的平分线。(1)已知∠POC=21 °,求∠AOC的度数。(2)已知∠BOC=40 °,求∠COQ的度数。(3)∠AOB=82 ° 请指明∠POQ的度数,并说明理由 如图,已知∠1=103°24′28" ,∠2= 30°54",求∠1+∠2 和∠1-∠2 的度数 .∠1+∠2 = 103°24′28" +30°54" .所以∠1+∠2 = 133°25′22" .(82" = 1′22" )解:∠1 - ∠2 = 103°24′28" +30°54" .所以∠1-∠2 = 73°23′ 34"(24′28"= 23′88")解: 解: ∠1+ ∠2=22°17′+∠2=90° ∠3+∠4=124°15′+55°45′=180°计算:(1)若∠1=22°17′ ,∠2=67°43′, 求∠1+ ∠2?(2)若∠3=124°15′ , ∠4=55°45′,求∠3+ ∠4?如果两个角的和等于90 °,那么就说这两个角互为余角,简称互余.其中一个角叫做另一个角的余角.如果两个角的和等于180 °,那么就说这两个角互为补角,简称互补.其中一个角叫做另一个角的补角.∵∠α+∠β=90° ∴∠α与∠β互为余角∵∠α+∠β=180°∴∠α与∠β互为补角数学语言:在图(1)中,∠AOB=90°;在图⑵中,∠DSE=180°.写出互为余角、互为补角的角。解:∠AOC与∠BOC互为余角,∠DSF与∠ESF互为补角.一起探究1.如果∠1和∠2都是∠α的余角,那么∠1和∠2相等吗?试着说说理由.2.如果∠3和∠4都是∠β的补角,那么∠3和∠4相等吗?试着说说理由.性质:同角(或等角)的余角相等,同角(或等角)的补角相等1.如图,已知∠1+∠3=90°,∠2+∠3=90°,∠1+∠4=90°,请写出∠1,∠2,∠3,∠4中的等量关系,并试着说说理由.解:∠1=∠2,∠3=∠4.理由:因为∠1+∠3=90°,∠2+∠3=90°,所以∠1=∠2.因为∠1+∠3=90°,∠1+∠4=90°,所以∠3=∠4(同角的余角相等).2.如图,直线AB与∠COD的两边OC,OD分别相交于点E,F,∠1+∠2=180°. 找出图中与∠2相等的角,并说明理由.解:因为∠1+∠3=180°,∠1+∠2=180°,所以∠3=∠2.因为∠1+∠4=180°,∠1+∠2=180°,所以∠4=∠2.因为∠2+∠5=180°,∠6+∠5=180°,所以∠2=∠6.所以图中与∠2相等的角有∠3,∠4,∠6.本节课探究了角哪些问题?在探究角的和差与相关性质时,你经历了什么?积累了哪些活动经验?完成课后习题+练习册.
相关资料
更多









