高考数学科学创新复习方案提升版第45讲直线的倾斜角与斜率、直线的方程学案（Word版附解析）

这是一份高考数学科学创新复习方案提升版第45讲直线的倾斜角与斜率、直线的方程学案（Word版附解析），共17页。

[课程标准]1.理解直线的倾斜角和斜率的概念，经历用代数方法刻画直线斜率的过程，掌握过两点的直线斜率的计算公式.2.掌握直线方程的几种形式(点斜式、斜截式、两点式、截距式及一般式)．
1．直线的方向向量
设A，B是直线上的两点，则eq \(AB,\s\up6(→))就是这条直线的方向向量．
2．直线的倾斜角与斜率
(1)直线的倾斜角
①定义：当直线l与x轴相交时，以x轴为基准，x轴eq \x(\s\up1(01))正向与直线leq \x(\s\up1(02))向上的方向之间所成的角α叫做这条直线的倾斜角．当直线l与x轴平行或重合时，规定它的倾斜角为eq \x(\s\up1(03))0°．
②倾斜角的范围为eq \x(\s\up1(04))0°≤α<180°．
(2)直线的斜率
3.直线的方向向量同斜率的关系
若直线l的斜率为k，它的一个方向向量的坐标为(x，y)，则k＝eq \x(\s\up1(07))eq \f(y,x)．
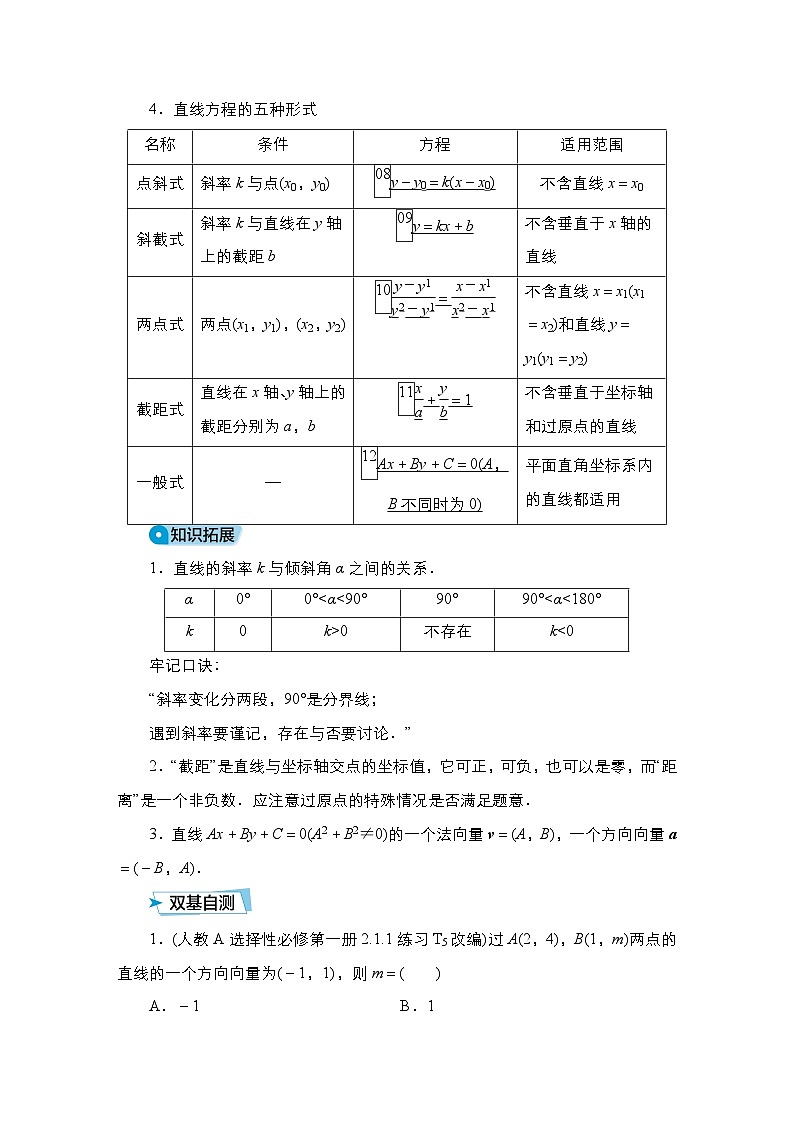
4．直线方程的五种形式
1．直线的斜率k与倾斜角α之间的关系．
牢记口诀：
“斜率变化分两段，90°是分界线；
遇到斜率要谨记，存在与否要讨论．”
2．“截距”是直线与坐标轴交点的坐标值，它可正，可负，也可以是零，而“距离”是一个非负数．应注意过原点的特殊情况是否满足题意．
3．直线Ax＋By＋C＝0(A2＋B2≠0)的一个法向量v＝(A，B)，一个方向向量a＝(－B，A)．
1．(人教A选择性必修第一册2.1.1练习T5改编)过A(2，4)，B(1，m)两点的直线的一个方向向量为(－1，1)，则m＝( )
A．－1 B．1
C．5 D．3
答案 C
解析 解法一：由题意可知eq \f(m－4,1－2)＝－1，∴m＝5.故选C.
解法二：∵eq \(AB,\s\up6(→))＝(－1，m－4)，∴m－4＝1，即m＝5.故选C.
2．直线x＋eq \r(3)y＋1＝0的倾斜角是( )
A.eq \f(π,6) B.eq \f(π,3)
C.eq \f(2π,3) D.eq \f(5π,6)
答案 D
解析 由直线的方程得直线的斜率k＝－eq \f(\r(3),3)，设该直线的倾斜角为α，则tanα＝－eq \f(\r(3),3)，又α∈[0，π)，所以α＝eq \f(5π,6).
3．(人教A选择性必修第一册练习T3改编)倾斜角为135°，在y轴上的截距为－1的直线方程是( )
A．x－y＋1＝0 B．x－y－1＝0
C．x＋y－1＝0 D．x＋y＋1＝0
答案 D
解析 直线的斜率为k＝tan135°＝－1，所以直线方程为y＝－x－1，即x＋y＋1＝0.
4．(人教A选择性必修第一册习题2.2 T10改编)如果AC＜0且BC＜0，那么直线Ax＋By＋C＝0不经过( )
A．第一象限 B．第二象限
C．第三象限 D．第四象限
答案 C
解析 ∵AC＜0，BC＜0，∴A，B同号．又直线Ax＋By＋C＝0可化为y＝－eq \f(A,B)x－eq \f(C,B)，－eq \f(A,B)＜0，－eq \f(C,B)＞0，∴直线Ax＋By＋C＝0不经过第三象限．
5．(人教A选择性必修第一册习题2.2 T7改编)过点(5，2)且在y轴上的截距是在x轴上的截距的2倍的直线方程是________．
答案 2x＋y－12＝0或2x－5y＝0
解析 设所求直线在x轴上的截距为a，则在y轴上的截距为2a.①当a＝0时，所求直线经过点(5，2)和(0，0)，所以直线方程为y＝eq \f(2,5)x，即2x－5y＝0；②当a≠0时，设所求直线方程为eq \f(x,a)＋eq \f(y,2a)＝1，又直线过点(5，2)，所以eq \f(5,a)＋eq \f(2,2a)＝1，解得a＝6，所以所求直线方程为eq \f(x,6)＋eq \f(y,12)＝1，即2x＋y－12＝0.综上，所求直线方程为2x－5y＝0或2x＋y－12＝0.
例1 (1)直线xsinα＋y＋2＝0的倾斜角的取值范围是( )
A．[0，π) B.eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,4)))∪eq \b\lc\[\rc\)(\a\vs4\al\c1(\f(3π,4)，π))
C.eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,4))) D.eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,4)))∪eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)，π))
答案 B
解析 设直线的倾斜角为θ，则有tanθ＝－sinα.因为sinα∈[－1，1]，所以－1≤tanθ≤1，又θ∈[0，π)，所以0≤θ≤eq \f(π,4)或eq \f(3π,4)≤θ＜π.故选B.
(2)(2023·湖北名校联考模拟)已知点A(2，3)，B(－3，－2)与直线l：kx－y－k＋1＝0，且直线l与线段AB相交，则直线l的斜率k的取值范围为________．
答案 eq \b\lc\(\rc\](\a\vs4\al\c1(－∞，\f(3,4)))∪[2，＋∞)
解析 已知点A(2，3)，B(－3，－2)与直线l：kx－y－k＋1＝0，且直线l与线段AB相交，直线l：kx－y－k＋1＝0，即直线l：k(x－1)－y＋1＝0，它经过定点M(1，1)，MA的斜率为eq \f(3－1,2－1)＝2，MB的斜率为eq \f(－2－1,－3－1)＝eq \f(3,4)，则直线l的斜率k的取值范围为eq \b\lc\(\rc\](\a\vs4\al\c1(－∞，\f(3,4)))∪[2，＋∞)．
直线倾斜角的范围是[0，π)，而这个区间不是正切函数的单调区间，因此根据斜率求倾斜角的范围时，要分eq \b\lc\[\rc\)(\a\vs4\al\c1(0，\f(π,2)))与eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)，π))两种情况讨论．
1.(2023·重庆南开中学模拟)已知直线l的一个方向向量为p＝eq \b\lc\(\rc\)(\a\vs4\al\c1(sin\f(π,3)，cs\f(π,3)))，则直线l的倾斜角为( )
A.eq \f(π,6) B.eq \f(π,3)
C.eq \f(2π,3) D.eq \f(4π,3)
答案 A
解析 由题意得，直线l的斜率k＝eq \f(cs\f(π,3),sin\f(π,3))＝eq \f(\r(3),3)＝taneq \f(π,6)，即直线l的倾斜角为eq \f(π,6).故选A.
2．若正方形一条对角线所在直线的斜率为2，则该正方形的两条邻边所在直线的斜率分别为________，________．
答案 eq \f(1,3) －3
解析 如图，在正方形OABC中，对角线OB所在直线的斜率为2，建立如图所示的平面直角坐标系．设对角线OB所在直线的倾斜角为θ，则tanθ＝2，由正方形的性质可知，直线OA的倾斜角为θ－45°，直线OC的倾斜角为θ＋45°，故kOA＝tan(θ－45°)＝eq \f(tanθ－tan45°,1＋tanθtan45°)＝eq \f(2－1,1＋2)＝eq \f(1,3)，kOC＝tan(θ＋45°)＝eq \f(tanθ＋tan45°,1－tanθtan45°)＝eq \f(2＋1,1－2)＝－3.
例2 求适合下列条件的直线方程：
(1)经过点P(1，2)，倾斜角α的正弦值为eq \f(4,5)；
(2)经过点P(2，3)，并且在两坐标轴上的截距相等；
(3)经过两条直线l1：x＋y＝2，l2：2x－y＝1的交点，且直线的一个方向向量为v＝(－3，2)．
解 (1)由题可知sinα＝eq \f(4,5)，则tanα＝±eq \f(4,3)，
∵直线经过点P(1，2)，∴直线的方程为y－2＝±eq \f(4,3)(x－1)，
即y＝±eq \f(4,3)(x－1)＋2，
整理得4x－3y＋2＝0或4x＋3y－10＝0.
(2)解法一：①当截距为0时，直线过点(0，0)，(2，3)，
则直线的斜率为k＝eq \f(3－0,2－0)＝eq \f(3,2)，
因此直线的方程为y＝eq \f(3,2)x，即3x－2y＝0.
②当截距不为0时，可设直线的方程为eq \f(x,a)＋eq \f(y,a)＝1.
∵直线过点P(2，3)，∴eq \f(2,a)＋eq \f(3,a)＝1，∴a＝5.
∴直线的方程为x＋y－5＝0.
综上可知，直线的方程为3x－2y＝0或x＋y－5＝0.
解法二：由题意可知所求直线的斜率存在，
则可设直线方程为y－3＝k(x－2)，且k≠0.
令x＝0，得y＝－2k＋3.
令y＝0，得x＝－eq \f(3,k)＋2.
于是－2k＋3＝－eq \f(3,k)＋2，解得k＝eq \f(3,2)或k＝－1.
则直线的方程为y－3＝eq \f(3,2)(x－2)或y－3＝－(x－2)，
即3x－2y＝0或x＋y－5＝0.
(3)联立eq \b\lc\{(\a\vs4\al\c1(x＋y＝2，,2x－y＝1，))解得eq \b\lc\{(\a\vs4\al\c1(x＝1，,y＝1，))∴直线过点(1，1)，
∵直线的一个方向向量为v＝(－3，2)，
∴直线的斜率k＝－eq \f(2,3).
则直线的方程为y－1＝－eq \f(2,3)(x－1)，即2x＋3y－5＝0.
求直线方程的两种方法
注意：使用点斜式、截距式求直线方程时，应注意分类讨论．
1.(2024·福建龙岩质检)过点A(－1，1)的直线l的倾斜角是直线l1：eq \r(3)x－y＋1＝0的倾斜角的2倍，则直线l的方程是( )
A.eq \r(3)x－y＋eq \r(3)＋1＝0B.eq \r(3)x＋y＋eq \r(3)－1＝0
C.eq \r(3)x－3y＋eq \r(3)＋3＝0D.eq \r(3)x＋3y＋eq \r(3)－3＝0
答案 B
解析 由k1＝tanα＝eq \r(3)，得α＝60°，所以k＝tan120°＝－eq \r(3)，所以直线l的方程是y－1＝－eq \r(3)(x＋1)，即eq \r(3)x＋y＋eq \r(3)－1＝0.
2．经过A(0，2)，B(－1，0)两点的直线方程为________，若直线的一个方向向量为(1，k)，则k＝________．
答案 2x－y＋2＝0 2
解析 经过A(0，2)，B(－1，0)两点的直线方程为eq \f(x,－1)＋eq \f(y,2)＝1，即2x－y＋2＝0，所以直线的一个方向向量为(1，2)，故k＝2.
3．过点P(6，－2)，且在x轴上的截距比在y轴上的截距大1的直线方程为________．
答案 2x＋3y－6＝0或x＋2y－2＝0
解析 设直线方程的截距式为eq \f(x,a＋1)＋eq \f(y,a)＝1，则eq \f(6,a＋1)＋eq \f(－2,a)＝1，解得a＝2或a＝1，则直线的方程是eq \f(x,3)＋eq \f(y,2)＝1或eq \f(x,2)＋eq \f(y,1)＝1，即2x＋3y－6＝0或x＋2y－2＝0.
多角度探究突破
角度 直线方程与不等式的结合
例3 过点P(4，1)作直线l，分别交x轴、y轴的正半轴于点A，B.
(1)当△AOB的面积最小时，求直线l的方程；
(2)当|OA|＋|OB|取最小值时，求直线l的方程．
解 设直线l：eq \f(x,a)＋eq \f(y,b)＝1(a>0，b>0)，因为直线l经过点P(4，1)，所以eq \f(4,a)＋eq \f(1,b)＝1.
(1)因为eq \f(4,a)＋eq \f(1,b)＝1≥2eq \r(\f(4,a)·\f(1,b))＝eq \f(4,\r(ab))，
所以ab≥16，S△AOB＝eq \f(1,2)ab≥8，
当且仅当a＝8，b＝2时等号成立．
所以当a＝8，b＝2时，△AOB的面积最小，
此时直线l的方程为eq \f(x,8)＋eq \f(y,2)＝1，即x＋4y－8＝0.
(2)因为eq \f(4,a)＋eq \f(1,b)＝1，a>0，b>0，所以|OA|＋|OB|＝a＋b＝(a＋b)eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(4,a)＋\f(1,b)))＝5＋eq \f(a,b)＋eq \f(4b,a)≥9，
当且仅当a＝6，b＝3时等号成立．
所以当|OA|＋|OB|取最小值时，直线l的方程为eq \f(x,6)＋eq \f(y,3)＝1，即x＋2y－6＝0.
角度 直线方程与函数的结合
例4 为了绿化城市，拟在矩形区域ABCD内建一个矩形草坪(如图)，另外△EFA内部有一文物保护区不能占用，经测量|AB|＝100 m，|BC|＝80 m，|AE|＝30 m，|AF|＝20 m，应如何设计才能使草坪面积最大？
解 如图所示，以A为坐标原点建立平面直角坐标系，则E(30，0)，F(0，20)，
∴直线EF的方程为eq \f(x,30)＋eq \f(y,20)＝1(0≤x≤30)．
易知当矩形草坪的一个顶点在线段EF上时，草坪面积可取最大值，
在线段EF上取点P(m，n)，作PQ⊥BC于点Q，PR⊥CD于点R，
设矩形PQCR的面积为S，
则S＝|PQ|·|PR|＝(100－m)(80－n)．
又eq \f(m,30)＋eq \f(n,20)＝1(0≤m≤30)，∴n＝20－eq \f(2,3)m.
∴S＝(100－m)eq \b\lc\(\rc\)(\a\vs4\al\c1(80－20＋\f(2,3)m))＝－eq \f(2,3)(m－5)2＋eq \f(18050,3)(0≤m≤30)．
∴当m＝5时，S有最大值，这时|EP|∶|PF|＝5∶1.
∴当矩形草坪的两边在BC，CD上，一个顶点在线段EF上，且这个顶点分有向线段EF成5∶1时，草坪面积最大．
直线方程综合问题的两大类型及解法
(1)与函数相结合的问题：解决这类问题，一般是利用直线方程中x，y的关系，将问题转化为关于x(或y)的函数，借助函数的性质解决．
(2)与方程、不等式相结合的问题：一般是利用方程、不等式的有关知识(如方程解的个数、根的存在问题、不等式的性质、基本不等式等)来解决．
1.已知直线l1：ax－2y＝2a－4，l2：2x＋a2y＝2a2＋4，当0＜a＜2时，直线l1，l2与两坐标轴围成一个四边形，当四边形的面积最小时，实数a＝________．
答案 eq \f(1,2)
解析 由题意知直线l1，l2恒过定点P(2，2)，直线l1在y轴上的截距为2－a，直线l2在x轴上的截距为a2＋2，所以四边形的面积S＝eq \f(1,2)×2×(2－a)＋eq \f(1,2)×2×(a2＋2)＝a2－a＋4＝eq \b\lc\(\rc\)(\a\vs4\al\c1(a－\f(1,2)))eq \s\up12(2)＋eq \f(15,4)，所以当a＝eq \f(1,2)时，四边形的面积最小．
2．如图，在两条互相垂直的道路l1，l2的一角有一个电线杆，电线杆底部到道路l1的垂直距离为4米，到道路l2的垂直距离为3米，现在要过电线杆的底部靠近道路的一侧修建一条人行直道，使得人行直道与两条垂直的道路围成的直角三角形的面积最小，则人行直道的长度为多少米？
解 如图，建立平面直角坐标系，则P(3，4)．
设人行道所在直线方程为y－4＝k(x－3)(k<0)，所以Aeq \b\lc\(\rc\)(\a\vs4\al\c1(3－\f(4,k)，0))，B(0，4－3k)，
所以△ABO的面积S＝eq \f(1,2)(4－3k)eq \b\lc\(\rc\)(\a\vs4\al\c1(3－\f(4,k)))＝eq \f(1,2)eq \b\lc\(\rc\)(\a\vs4\al\c1(24－9k－\f(16,k)))，
因为k<0，所以－9k－eq \f(16,k)≥2eq \r(（－9k）\b\lc\(\rc\)(\a\vs4\al\c1(－\f(16,k))))＝24，
当且仅当－9k＝－eq \f(16,k)，即k＝－eq \f(4,3)时取等号．此时，A(6，0)，B(0，8)，所以人行直道的长度为eq \r(62＋82)＝10米．
课时作业
一、单项选择题
1．(2023·上海松江区二模)经过点(1，1)，且方向向量为(1，2)的直线方程是( )
A．2x－y－1＝0 B．2x＋y－3＝0
C．x－2y＋1＝0 D．x＋2y－3＝0
答案 A
解析 由于直线的方向向量为(1，2)，故直线的斜率为eq \f(2,1)＝2，故直线的方程为y－1＝2(x－1)，即2x－y－1＝0.故选A.
2．(2024·山东滨州模拟)已知A(m，0)，B(0，1)，C(3，－1)，且A，B，C三点共线，则m＝( )
A.eq \f(3,2) B.eq \f(2,3)
C．－eq \f(3,2) D．－eq \f(2,3)
答案 A
解析 因为A，B，C三点共线，且A(m，0)，B(0，1)，C(3，－1)，所以直线的斜率存在，且kAB＝kBC，即eq \f(1,－m)＝eq \f(－2,3)，解得m＝eq \f(3,2).故选A.
3．(2023·杭州学军中学期中)已知直线l1：eq \r(3)x＋y＝0与直线l2：kx－y＋1＝0，若直线l1与直线l2的夹角为60°，则实数k的值为( )
A.eq \r(3) B．－eq \r(3)
C.eq \r(3)或0 D．－eq \r(2)或－eq \r(3)
答案 C
解析 因为直线l1：eq \r(3)x＋y＝0的斜率为k＝－eq \r(3)，所以其倾斜角为120°.直线l2：kx－y＋1＝0恒过点(0，1)，如图，若直线l1与直线l2的夹角为60°，则l2的倾斜角为60°或0°，所以k＝eq \r(3)或k＝0.故选C.
4．函数f(x)＝eq \f(1,3)x3－x2的图象上有一动点，则在此动点处切线的倾斜角的取值范围为( )
A.eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(3π,4))) B.eq \b\lc\[\rc\)(\a\vs4\al\c1(0，\f(π,2)))∪eq \b\lc\[\rc\)(\a\vs4\al\c1(\f(3π,4)，π))
C.eq \b\lc\[\rc\)(\a\vs4\al\c1(\f(3π,4)，π)) D.eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,2)，\f(3π,4)))
答案 B
解析 设切线的倾斜角为α，则α∈[0，π)，∵f′(x)＝x2－2x＝(x－1)2－1≥－1，∴切线的斜率k＝tanα≥－1，则α的取值范围为eq \b\lc\[\rc\)(\a\vs4\al\c1(0，\f(π,2)))∪eq \b\lc\[\rc\)(\a\vs4\al\c1(\f(3π,4)，π)).
5．已知△ABC的顶点C的坐标为(1，1)，AC所在直线的方向向量为(1，2)，AC边上的中线所在的直线方程为x＋y－1＝0，则点A的坐标为( )
A.eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3)，－\f(1,3))) B.eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2,3)，－\f(1,3)))
C.eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2,3)，－\f(2,3))) D.eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3)，－\f(2,3)))
答案 A
解析 设A(x0，y0)，AC所在直线的方向向量为(1，2)，则AC所在直线的斜率k＝eq \f(1－y0,1－x0)＝eq \f(2,1)，∴1×(1－y0)－2(1－x0)＝0，得y0＝2x0－1，∴A(x0，2x0－1)，又C(1，1)，则AC的中点坐标为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1＋x0,2)，x0))，∵AC边上的中线所在的直线方程为x＋y－1＝0，则AC的中点eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1＋x0,2)，x0))在直线x＋y－1＝0上，∴eq \f(1＋x0,2)＋x0－1＝0，解得x0＝eq \f(1,3)，∴点A的坐标为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3)，－\f(1,3))).故选A.
6．现有下列四个命题：
甲：直线l经过点(0，－1)；
乙：直线l经过点(1，0)；
丙：直线l经过点(－1，1)；
丁：直线l的倾斜角为锐角．
如果只有一个假命题，则假命题是( )
A．甲 B．乙
C．丙 D．丁
答案 C
解析 设A(0，－1)，B(1，0)，C(－1，1)，则kAB＝eq \f(－1－0,0－1)＝1，kBC＝eq \f(1－0,－1－1)＝－eq \f(1,2)，因为kAB≠kBC，所以A，B，C三点不共线，所以假命题必是甲、乙、丙中的一个，丁是真命题，即直线l的斜率大于0，而kAB>0，kBC<0，kAC<0，故丙是假命题．故选C.
7．(2024·四川宜宾模拟)若直线ax＋by＝ab(a>0，b>0)过点(1，1)，则该直线在x轴与y轴上的截距之和的最小值为( )
A．1 B．2
C．3 D．4
答案 D
解析 因为直线ax＋by＝ab过点(1，1)，所以a＋b＝ab，又因为a>0，b>0，所以eq \f(1,b)＋eq \f(1,a)＝1，所以直线eq \f(x,b)＋eq \f(y,a)＝1在x轴与y轴上的截距之和为b＋a＝(b＋a)eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,b)＋\f(1,a)))＝2＋eq \f(a,b)＋eq \f(b,a)≥2＋2eq \r(\f(a,b)·\f(b,a))＝4，当且仅当eq \f(a,b)＝eq \f(b,a)，即a＝b＝2时取等号，所以直线在x轴与y轴上的截距之和的最小值为4.故选D.
8.(2023·安徽江南十校模拟)1949年公布的《国旗制法说明》中就五星的位置规定：大五角星有一个角尖正向上方，四颗小五角星均各有一个角尖正对大五角星的中心点．有人发现，第三颗小星的姿态与大星相近．为便于研究，如图，以大星的中心点为原点，建立平面直角坐标系，OO1，OO2，OO3，OO4分别是大星中心点与四颗小星中心点的连接线，α≈16°，则第三颗小星的一条边AB所在直线的倾斜角约为( )
A．0° B．1°
C．2° D．3°
答案 C
解析 ∵O，O3都为五角星的中心点，∴OO3平分第三颗小星的一个角，由五角星的内角为36°，知∠BAO3＝18°，过O3作x轴的平行线O3E，如图，则∠OO3E＝α≈16°，∴直线AB的倾斜角约为18°－16°＝2°.故选C.
二、多项选择题
9．已知直线l过点P(3，2)，且与直线l1：x＋3y－9＝0及x轴围成一个底边在x轴上的等腰三角形，则( )
A．直线l的方程为x－3y＋3＝0
B．直线l与直线l1的倾斜角互补
C．直线l在y轴上的截距为1
D．这样的直线l有两条
答案 ABC
解析 因为直线l与l1及x轴围成一个底边在x轴上的等腰三角形，所以直线l与直线l1的倾斜角互补，故B正确；由直线l1的斜率为－eq \f(1,3)，知直线l的斜率为eq \f(1,3)，可得直线l的方程为y－2＝eq \f(1,3)(x－3)，即直线l的方程为x－3y＋3＝0，故A正确；令x＝0，得y＝1，所以直线l在y轴上的截距为1，故C正确；过点P(3，2)且斜率为eq \f(1,3)的直线只有一条，故D错误．故选ABC.
10．已知直线xsinα＋ycsα＋1＝0(α∈R)，则下列命题正确的是( )
A．直线的倾斜角是π－α
B．无论α如何变化，直线不过原点
C．直线的斜率一定存在
D．当直线和两坐标轴都相交时，它和坐标轴围成的三角形的面积不小于1
答案 BD
解析 直线倾斜角的范围为[0，π)，而π－α∈R，A不正确；当x＝y＝0时，xsinα＋ycsα＋1＝1≠0，所以直线必不过原点，B正确；当α＝eq \f(π,2)时，直线的斜率不存在，C不正确；当直线和两坐标轴都相交时，它和坐标轴围成的三角形的面积为S＝eq \f(1,2)eq \b\lc\|\rc\|(\a\vs4\al\c1(\f(1,－sinα)))·eq \b\lc\|\rc\|(\a\vs4\al\c1(\f(1,－csα)))＝eq \f(1,|sin2α|)≥1，D正确．故选BD.
11．(2023·广东珠海二模)在平面直角坐标系中，已知正方形ABCD四边所在直线与x轴的交点分别为(0，0)，(1，0)，(2，0)，(4，0)，则正方形ABCD四边所在直线中过点(0，0)的直线的斜率可以是( )
A．2 B.eq \f(3,2)
C.eq \f(3,4) D.eq \f(1,4)
答案 ABD
解析 因为选项斜率均为正值，不妨假设AB所在的直线过点(0，0)，设直线AB的倾斜角为α∈eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(π,2)))，斜率为k，①若CD所在的直线过点(1，0)，如图1，可得|BC|＝sinα，|CD|＝2csα，因为|BC|＝|CD|，即sinα＝2csα，所以k＝tanα＝2；②若CD所在的直线过点(2，0)，如图2，可得|BC|＝2sinα，|CD|＝3csα，因为|BC|＝|CD|，即2sinα＝3csα，所以k＝tanα＝eq \f(3,2)；③若CD所在的直线过点(4，0)，如图3，可得|BC|＝4sinα，|CD|＝csα，因为|BC|＝|CD|，即4sinα＝csα，所以k＝tanα＝eq \f(1,4).综上所述，k的值可能为2，eq \f(3,2)，eq \f(1,4).故选ABD.
三、填空题
12．若直线l的一个方向向量为a＝eq \b\lc\(\rc\)(\a\vs4\al\c1(sin\f(π,7)，cs\f(π,7)))，则直线l的倾斜角θ＝________．
答案 eq \f(5π,14)
解析 ∵直线l的一个方向向量为a＝eq \b\lc\(\rc\)(\a\vs4\al\c1(sin\f(π,7)，cs\f(π,7)))，∴直线l的斜率k＝eq \f(cs\f(π,7),sin\f(π,7))＝eq \f(sin\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)－\f(π,7))),cs\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)－\f(π,7))))＝eq \f(sin\f(5π,14),cs\f(5π,14))＝taneq \f(5π,14)，∴直线l的倾斜角θ＝eq \f(5π,14).
13．在△ABC中，已知A(1，1)，AC边上的高线所在的直线方程为x－2y＝0，AB边上的高线所在的直线方程为3x＋2y－3＝0.则BC边所在的直线方程为________．
答案 2x＋5y＋9＝0
解析 由题意，得kAC＝－2，kAB＝eq \f(2,3)，∴lAC：y－1＝－2(x－1)，即2x＋y－3＝0，lAB：y－1＝eq \f(2,3)(x－1)，即2x－3y＋1＝0.由eq \b\lc\{(\a\vs4\al\c1(2x＋y－3＝0，,3x＋2y－3＝0，))得C(3，－3)．由eq \b\lc\{(\a\vs4\al\c1(2x－3y＋1＝0，,x－2y＝0，))得B(－2，－1)，∴lBC：2x＋5y＋9＝0.
14．(2023·重庆育才中学期末)在平面直角坐标系中，O为坐标原点．设△ABC的顶点分别为A(0，a)，B(b，0)，C(c，0)，点P(0，p)在线段AO上(异于端点)，设a，b，c，p均为非零实数，直线BP，CP分别交AC，AB于点E，F，一同学已正确算得OE的方程：eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,b)－\f(1,c)))x＋eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,p)－\f(1,a)))y＝0，则OF的方程为________________．
答案 eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,b)－\f(1,c)))x－eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,p)－\f(1,a)))y＝0
解析 由题意，C(c，0)，P(0，p)，则CP的方程为eq \f(x,c)＋eq \f(y,p)＝1，同理，AB的方程为eq \f(x,b)＋eq \f(y,a)＝1，两直线方程相减，得OF的方程为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,b)－\f(1,c)))x－eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,p)－\f(1,a)))y＝0.
四、解答题
15．已知△ABC的三个顶点分别为A(－3，0)，B(2，1)，C(－2，3)，求：
(1)BC边所在直线的方程；
(2)BC边的垂直平分线DE的方程．
解 (1)因为直线BC经过B(2，1)和C(－2，3)两点，
所以直线BC的方程为eq \f(y－1,3－1)＝eq \f(x－2,－2－2)，即x＋2y－4＝0.
(2)由(1)知，直线BC的斜率k1＝－eq \f(1,2)，
则直线BC的垂直平分线DE的斜率k2＝2.
因为BC边的垂直平分线DE经过BC的中点(0，2)，
所以所求直线方程为y－2＝2(x－0)，即2x－y＋2＝0.
16．过点Peq \b\lc\(\rc\)(\a\vs4\al\c1(\f(4,3)，2))的直线l与x轴的正半轴、y轴的正半轴分别交于A，B两点，O为坐标原点．
(1)求△OAB面积的最小值以及此时直线l的方程；
(2)是否存在直线l，使△OAB的周长为12？若存在，求出直线l的方程；若不存在，说明理由．
解 (1)设A(a，0)，B(0，b)(a>0，b>0)，
则直线l的方程为eq \f(x,a)＋eq \f(y,b)＝1.
因为直线l过点Peq \b\lc\(\rc\)(\a\vs4\al\c1(\f(4,3)，2))，所以eq \f(4,3a)＋eq \f(2,b)＝1，
故1＝eq \f(4,3a)＋eq \f(2,b)≥2eq \r(\f(8,3ab))⇒ab≥eq \f(32,3)，故S△OAB＝eq \f(1,2)ab≥eq \f(16,3)，
当且仅当eq \b\lc\{(\a\vs4\al\c1(\f(4,3a)＝\f(2,b)，,\f(4,3a)＋\f(2,b)＝1，))即eq \b\lc\{(\a\vs4\al\c1(a＝\f(8,3)，,b＝4))时取等号，此时直线l的方程为eq \f(3x,8)＋eq \f(y,4)＝1，故(S△OAB)min＝eq \f(16,3)，此时直线l的方程为3x＋2y－8＝0.
(2)假设存在满足条件的直线l：eq \f(x,a)＋eq \f(y,b)＝1(a>0，b>0)，
由已知得eq \b\lc\{(\a\vs4\al\c1(\f(4,3a)＋\f(2,b)＝1，,a＋b＋\r(a2＋b2)＝12，))
解得eq \b\lc\{(\a\vs4\al\c1(a＝4，,b＝3))或eq \b\lc\{(\a\vs4\al\c1(a＝\f(12,5)，,b＝\f(9,2)，))
故存在满足条件的直线l：3x＋4y－12＝0或15x＋8y－36＝0.条件
公式
直线的倾斜角为α，且α≠90°
k＝eq \x(\s\up1(05))tanα
直线过点A(x1，y1)，B(x2，y2)，且x1≠x2
k＝eq \x(\s\up1(06))eq \f(y2－y1,x2－x1)
名称
条件
方程
适用范围
点斜式
斜率k与点(x0，y0)
eq \x(\s\up1(08))y－y0＝k(x－x0)
不含直线x＝x0
斜截式
斜率k与直线在y轴上的截距b
eq \x(\s\up1(09))y＝kx＋b
不含垂直于x轴的直线
两点式
两点(x1，y1)，(x2，y2)
eq \x(\s\up1(10))eq \f(y－y1,y2－y1)＝eq \f(x－x1,x2－x1)
不含直线x＝x1(x1＝x2)和直线y＝y1(y1＝y2)
截距式
直线在x轴、y轴上的截距分别为a，b
eq \x(\s\up1(11))eq \f(x,a)＋eq \f(y,b)＝1
不含垂直于坐标轴和过原点的直线
一般式
—
eq \x(\s\up1(12))Ax＋By＋C＝0(A，B不同时为0)
平面直角坐标系内的直线都适用
α
0°
0°<α<90°
90°
90°<α<180°
k
0
k>0
不存在
k<0
考向一 直线的倾斜角与斜率
考向二 求直线的方程
考向三 直线方程的应用