

高考数学科学创新复习方案提升版第48讲直线与圆、圆与圆的位置关系学案(Word版附解析)
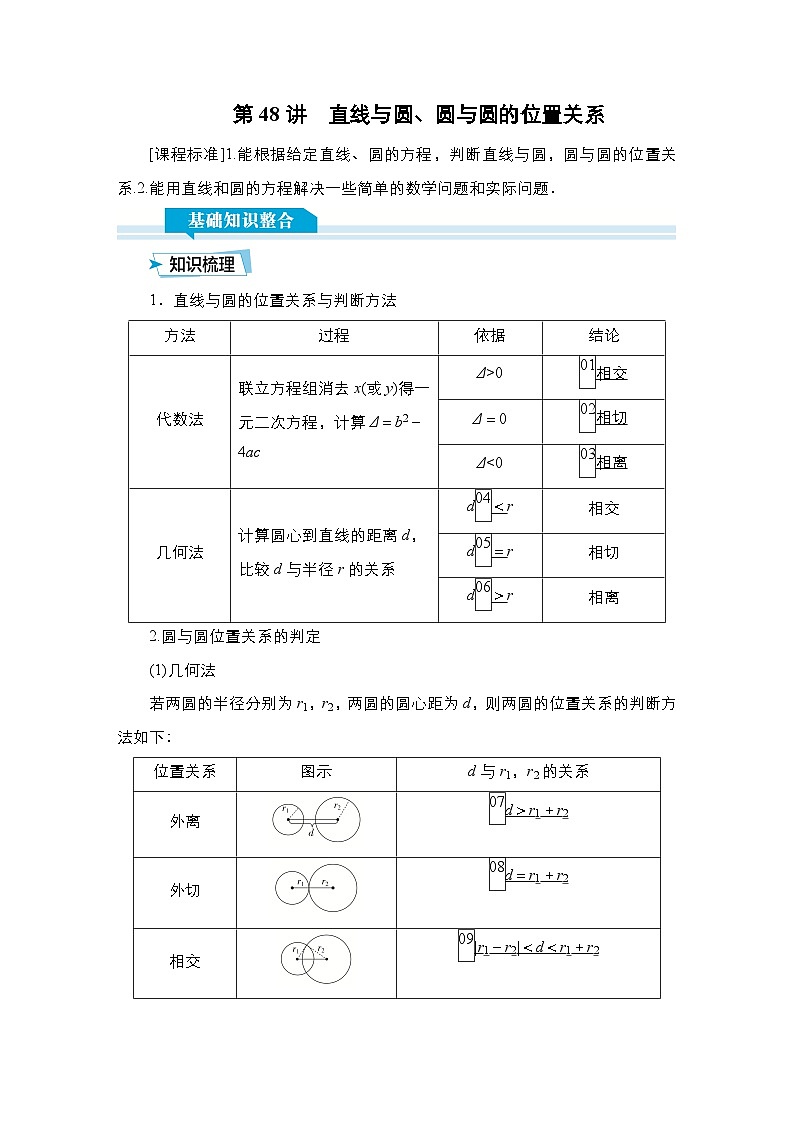
展开1.直线与圆的位置关系与判断方法
2.圆与圆位置关系的判定
(1)几何法
若两圆的半径分别为r1,r2,两圆的圆心距为d,则两圆的位置关系的判断方法如下:
(2)代数法
通过两圆方程组成方程组的公共解的个数进行判断.
eq \b\lc\ \rc\}(\a\vs4\al\c1(圆C1方程,圆C2方程))eq \(――→,\s\up7(消元))eq \a\vs4\al(一元,二次,方程)eq \b\lc\{(\a\vs4\al\c1(Δ>0⇒\x(\s\up1(12))相交;,Δ=0⇒\x(\s\up1(13))内切或外切;,Δ<0⇒\x(\s\up1(14))内含或外离.))
1.圆的切线方程常用结论
(1)过圆x2+y2=r2上一点P(x0,y0)的圆的切线方程为x0x+y0y=r2.
(2)过圆(x-a)2+(y-b)2=r2上一点P(x0,y0)的圆的切线方程为(x0-a)(x-a)+(y0-b)(y-b)=r2.
(3)过圆x2+y2=r2外一点M(x0,y0)作圆的两条切线,则两切点所在直线方程为x0x+y0y=r2.
2.圆与圆的位置关系的常用结论
(1)两圆的位置关系与公切线的条数
①内含:0条;②内切:1条;③相交:2条;④外切:3条;⑤外离:4条.
(2)两圆相交时公共弦的方程
设圆C1:x2+y2+D1x+E1y+F1=0,①
圆C2:x2+y2+D2x+E2y+F2=0,②
若两圆相交,则有一条公共弦,其公共弦所在直线方程由①-②所得,即(D1-D2)x+(E1-E2)y+(F1-F2)=0.
(3)两个圆系方程
①过直线Ax+By+C=0与圆x2+y2+Dx+Ey+F=0交点的圆系方程为x2+y2+Dx+Ey+F+λ(Ax+By+C)=0(λ∈R);
②过圆C1:x2+y2+D1x+E1y+F1=0和圆C2:x2+y2+D2x+E2y+F2=0交点的圆系方程为x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0(λ≠-1)(其中不含圆C2,所以注意检验C2是否满足题意,以防丢解).
1.对任意的实数k,直线y=kx-1与圆C:x2+y2-2x-2=0的位置关系是( )
A.相离B.相切
C.相交D.以上三个选项均有可能
答案 C
解析 直线y=kx-1恒经过点A(0,-1),圆x2+y2-2x-2=0的圆心为C(1,0),半径为eq \r(3),而|AC|=eq \r(2)
A.eq \r(3) B.2
C.eq \r(6) D.2eq \r(3)
答案 D
解析 直线方程为y=eq \r(3)x,圆的标准方程为x2+(y-2)2=4,则圆心(0,2)到直线的距离d=eq \f(|\r(3)×0-2|,2)=1,所以所求弦长为2×eq \r(22-12)=2eq \r(3).
3.(人教B选择性必修第一册2.3.3练习B T1改编)圆Q:x2+y2-4x=0在点P(1,eq \r(3))处的切线方程为( )
A.x+eq \r(3)y-2=0 B.x+eq \r(3)y-4=0
C.x-eq \r(3)y+4=0 D.x-eq \r(3)y+2=0
答案 D
解析 圆Q的标准方程为(x-2)2+y2=4.∵P(1,eq \r(3))在圆Q上,∴所求切线方程为(1-2)(x-2)+(eq \r(3)-0)(y-0)=4,即x-eq \r(3)y+2=0.
4.(人教A选择性必修第一册2.5.2练习T1改编)圆C1:(x+2)2+(y-2)2=4和圆C2:(x-2)2+(y-5)2=16的位置关系是( )
A.外离 B.相交
C.内切 D.外切
答案 B
解析 易得圆C1的圆心为C1(-2,2),半径r1=2,圆C2的圆心为C2(2,5),半径r2=4,圆心距|C1C2|=eq \r([2-(-2)]2+(5-2)2)=5,因为|4-2|<|C1C2|<4+2,所以两圆相交.
5.(人教A选择性必修第一册习题2.5 T9改编)圆x2+y2-4=0与圆x2+y2-4x+4y-12=0的公共弦所在的直线方程为________.
答案 x-y+2=0
解析 将两圆方程相减,得4x-4y+8=0,即x-y+2=0.
例1 (1)直线kx-y+2-k=0与圆x2+y2-2x-8=0的位置关系为( )
A.相交、相切或相离 B.相交或相切
C.相交 D.相切
答案 C
解析 解法一:直线kx-y+2-k=0的方程可化为k(x-1)-(y-2)=0,该直线恒过定点(1,2).因为12+22-2×1-8<0,所以点(1,2)在圆x2+y2-2x-8=0的内部,所以直线kx-y+2-k=0与圆x2+y2-2x-8=0相交.
解法二:圆的方程可化为(x-1)2+y2=32,所以圆心为(1,0),半径为3.圆心到直线kx-y+2-k=0的距离为eq \f(|k+2-k|,\r(1+k2))=eq \f(2,\r(1+k2))≤2<3,所以直线kx-y+2-k=0与圆x2+y2-2x-8=0相交.
(2)(2022·新高考Ⅱ卷)设点A(-2,3),B(0,a),若直线AB关于y=a对称的直线与圆(x+3)2+(y+2)2=1有公共点,则a的取值范围是________.
答案 eq \b\lc\[\rc\](\a\vs4\al\c1(\f(1,3),\f(3,2)))
解析 A(-2,3)关于y=a对称的点的坐标为A′(-2,2a-3),B(0,a)在直线y=a上,设A′B所在直线为直线l,所以直线l的方程为y=eq \f(a-3,-2)x+a,即(a-3)x+2y-2a=0.圆C:(x+3)2+(y+2)2=1,圆心C(-3,-2),半径r=1,依题意,圆心到直线l的距离d=eq \f(|-3(a-3)-4-2a|,\r((a-3)2+22))≤1,即(5-5a)2≤(a-3)2+22,解得eq \f(1,3)≤a≤eq \f(3,2),即a的取值范围是eq \b\lc\[\rc\](\a\vs4\al\c1(\f(1,3),\f(3,2))).
1.判断直线与圆的位置关系的常见方法
2.已知直线与圆的位置关系求参数的取值范围时,可根据数形结合思想转化为直线与圆的位置关系问题,由此建立方程(组)或不等式(组)求解.
1.(多选)(2021·新高考Ⅱ卷)已知直线l:ax+by-r2=0与圆C:x2+y2=r2,点A(a,b),则下列说法正确的是( )
A.若点A在圆C上,则直线l与圆C相切
B.若点A在圆C内,则直线l与圆C相离
C.若点A在圆C外,则直线l与圆C相离
D.若点A在直线l上,则直线l与圆C相切
答案 ABD
解析 圆心C(0,0)到直线l的距离d=eq \f(r2,\r(a2+b2)),若点A(a,b)在圆C上,则a2+b2=r2,所以d=eq \f(r2,\r(a2+b2))=|r|,则直线l与圆C相切,故A正确;若点A(a,b)在圆C内,则a2+b2
2.已知圆O:x2+y2=4上到直线l:x+y=a的距离等于1的点至少有2个,则a的取值范围为________.
答案 (-3eq \r(2),3eq \r(2))
解析 由圆的方程可知圆心为(0,0),半径为2.因为圆上到直线l:x+y=a的距离等于1的点至少有2个,所以圆心到直线l的距离d<r+1=3,即d=eq \f(|-a|,\r(2))<3,解得-3eq \r(2)<a<3eq \r(2).
多角度探究突破
角度 圆的切线问题
例2 已知点P(eq \r(2)+1,2-eq \r(2)),点M(3,1),圆C:(x-1)2+(y-2)2=4.
(1)求过点P的圆C的切线方程;
(2)求过点M的圆C的切线方程,并求出切线长.
解 由题意,得圆心C(1,2),半径r=2.
(1)∵(eq \r(2)+1-1)2+(2-eq \r(2)-2)2=4,
∴点P在圆C上.
又kPC=eq \f(2-\r(2)-2,\r(2)+1-1)=-1,
∴切线的斜率k=-eq \f(1,kPC)=1,
∴过点P的圆C的切线方程是y-(2-eq \r(2))=1·[x-(eq \r(2)+1)],即x-y+1-2eq \r(2)=0.
(2)∵(3-1)2+(1-2)2=5>4,
∴点M在圆C外部.
当过点M的直线的斜率不存在时,直线方程为x=3,即x-3=0.
又点C(1,2)到直线x-3=0的距离d=3-1=2=r,
即此时满足题意,∴直线x-3=0是圆的切线;
当切线的斜率存在时,设切线方程为y-1=k(x-3),即kx-y+1-3k=0,则圆心C到切线的距离为d=eq \f(|k-2+1-3k|,\r(k2+1))=r=2,解得k=eq \f(3,4).
∴切线方程为y-1=eq \f(3,4)(x-3),即3x-4y-5=0.
综上可得,过点M的圆C的切线方程为x-3=0或3x-4y-5=0.
∵|MC|=eq \r((3-1)2+(1-2)2)=eq \r(5),
∴过点M的圆C的切线长为eq \r(|MC|2-r2)=eq \r(5-4)=1.
圆的切线方程的求法
(1)几何法:设切线方程为y-y0=k(x-x0),利用点到直线的距离公式表示出圆心到切线的距离d,然后令d=r,进而求出k.
(2)代数法:设切线方程为y-y0=k(x-x0),与圆的方程组成方程组,消元后得到一个一元二次方程,然后令判别式Δ=0,进而求出k.
注意检验切线斜率不存在的情况.
1.(2024·南京师大附中校考一模)过点P(3,-2)且与圆C:x2+y2-2x-4y+1=0相切的直线方程为________.
答案 x=3或3x+4y-1=0
解析 将圆C的一般方程化为标准方程,得(x-1)2+(y-2)2=4,则圆心C(1,2),半径为r=2.当过点P(3,-2)的直线斜率不存在时,直线方程为x=3,是圆C的切线,满足题意;当过点P(3,-2)的直线斜率存在时,可设直线方程为y+2=k(x-3),即kx-y-3k-2=0,利用圆心到直线的距离等于半径,得eq \f(|2k+4|,\r(k2+1))=2,解得k=-eq \f(3,4),即此直线方程为3x+4y-1=0.故所求直线方程为x=3或3x+4y-1=0.
2.(2023·天津和平区二模)由直线y=x+1上的一点向圆(x-3)2+y2=1引切线,则切线长的最小值为________.
答案 eq \r(7)
解析 设直线上一点P,切点为Q,圆心为M,M的坐标为(3,0),则|PQ|即为切线长,|MQ|为圆M的半径,长度为1,|PQ|=eq \r(|PM|2-|MQ|2)=eq \r(|PM|2-1),要使|PQ|最小,即求|PM|的最小值,此题转化为求直线y=x+1上的点到圆心M的最小距离.设圆心到直线y=x+1的距离为d,则d=eq \f(|3-0+1|,\r(12+(-1)2))=2eq \r(2),∴|PM|的最小值为2eq \r(2),此时|PQ|=eq \r(|PM|2-1)=eq \r((2\r(2))2-1)=eq \r(7).
角度 圆的弦长问题
例3 (1)过点(-4,0)作直线l与圆x2+y2+2x-4y-20=0交于A,B两点,若|AB|=8,则直线l的方程为( )
A.5x+12y+20=0
B.5x+12y+20=0或x+4=0
C.5x-12y+20=0
D.5x-12y+20=0或x+4=0
答案 B
解析 圆的标准方程为(x+1)2+(y-2)2=25,由|AB|=8知,圆心(-1,2)到直线l的距离d=eq \r(25-42)=3.当直线l的斜率不存在,即直线l的方程为x=-4时,符合题意;当直线l的斜率存在时,设直线l的方程为y=k(x+4),即kx-y+4k=0,则有eq \f(|3k-2|,\r(k2+1))=3,解得k=-eq \f(5,12),此时直线l的方程为5x+12y+20=0.综上,直线l的方程为5x+12y+20=0或x+4=0.
(2)(2023·新课标Ⅱ卷)已知直线l:x-my+1=0与⊙C:(x-1)2+y2=4交于A,B两点,写出满足“△ABC的面积为eq \f(8,5)”的m的一个值:________.
答案 2eq \b\lc\(\rc\)(\a\vs4\al\c1(2,-2,\f(1,2),-\f(1,2)中任意一个皆可以))
解析 设点C到直线AB的距离为d,由弦长公式得|AB|=2eq \r(4-d2),所以S△ABC=eq \f(1,2)×d×2eq \r(4-d2)=eq \f(8,5),解得d=eq \f(4\r(5),5)或d=eq \f(2\r(5),5),因为d=eq \f(|1+1|,\r(1+m2))=eq \f(2,\r(1+m2)),所以eq \f(2,\r(1+m2))=eq \f(4\r(5),5)或eq \f(2,\r(1+m2))=eq \f(2\r(5),5),解得m=±2或m=±eq \f(1,2).
求直线被圆截得的弦长的常用方法
(多选)已知圆C:(x-1)2+(y-1)2=16,直线l:(2m-1)x+(m-1)y-3m+1=0.下列说法正确的是( )
A.直线l恒过定点(2,1)
B.圆C被y轴截得的弦长为2eq \r(15)
C.直线l被圆C截得的弦长存在最大值,此时直线l的方程为2x+y-3=0
D.直线l被圆C截得的弦长存在最小值,此时直线l的方程为x-2y-4=0
答案 BD
解析 对于A,将直线l的方程整理为m(2x+y-3)+(-x-y+1)=0,由eq \b\lc\{(\a\vs4\al\c1(-x-y+1=0,,2x+y-3=0,))得eq \b\lc\{(\a\vs4\al\c1(x=2,,y=-1,))无论m为何值,直线l恒过定点(2,-1),故A不正确;对于B,将x=0代入圆C的方程,得(y-1)2=15,解得y=1±eq \r(15),故圆C被y轴截得的弦长为2eq \r(15),故B正确;对于C,无论m为何值,直线l不过圆心(1,1),即直线l被圆C截得的弦长不存在最大值,故C不正确;对于D,当截得的弦长最短时,直线l垂直于圆心与定点的连线,则直线l的斜率为eq \f(1,2),此时直线l的方程为y+1=eq \f(1,2)(x-2),即x-2y-4=0,故D正确.故选BD.
例4 (1)(2023·唐山二模)已知圆C1:x2+y2-2x=0,圆C2:(x-3)2+(y-1)2=4,则圆C1与C2的位置关系是( )
A.外切 B.内切
C.相交 D.外离
答案 C
解析 圆C1的圆心为(1,0),r1=1,圆C2的圆心为(3,1),r2=2,所以r2-r1<|C1C2|=eq \r((3-1)2+(1-0)2)=eq \r(5)
A.C1与C2的公切线恰有4条
B.C1与C2相交弦的方程为3x+4y-9=0
C.C1与C2相交弦的弦长为eq \f(12,5)
D.若P,Q分别是圆C1,C2上的动点,则|PQ|max=12
答案 BD
解析 由已知得圆C1的圆心C1(0,0),半径r1=3,圆C2的圆心C2(3,4),半径r2=4,|C1C2|=eq \r((3-0)2+(4-0)2)=5,r2-r1<|C1C2|
常用几何法,即用两圆圆心距与两圆半径和与差的绝对值的关系,一般不用代数法.
2.两圆公共弦长的求法
先求出公共弦所在直线的方程,在其中一圆中,由弦心距d,半弦长eq \f(l,2),半径r构成直角三角形,利用勾股定理求解.
1.已知圆C与圆x2+y2+10x+10y=0相切于原点,且过点A(0,-6),则圆C的标准方程为________.
答案 (x+3)2+(y+3)2=18
解析 设圆C的标准方程为(x-a)2+(y-b)2=r2,其圆心为C(a,b),半径为r(r>0).∵x2+y2+10x+10y=0可化为(x+5)2+(y+5)2=50,∴其圆心为(-5,-5),半径为5eq \r(2).∵两圆相切于原点O,且圆C过点(0,-6),点(0,-6)在圆(x+5)2+(y+5)2=50内,∴两圆内切,∴eq \b\lc\{(\a\vs4\al\c1(a2+b2=r2,,\r((a+5)2+(b+5)2)=5\r(2)-r,,(0-a)2+(-6-b)2=r2,))解得a=-3,b=-3,r=3eq \r(2),∴圆C的标准方程为(x+3)2+(y+3)2=18.
2.(2022·新高考Ⅰ卷)写出与圆x2+y2=1和(x-3)2+(y-4)2=16都相切的一条直线的方程:________.
答案 x=-1或7x-24y-25=0或3x+4y-5=0(填一个即可)
解析 如图,因为圆x2+y2=1的圆心为O(0,0),半径r1=1,圆(x-3)2+(y-4)2=16的圆心为A(3,4),半径r2=4,所以|OA|=5,r1+r2=5,所以|OA|=r1+r2,所以两圆外切,公切线有三种情况:①易知公切线l1的方程为x=-1;②另一条公切线l2与公切线l1关于过两圆圆心的直线l对称.易知过两圆圆心的直线l的方程为y=eq \f(4,3)x,由eq \b\lc\{(\a\vs4\al\c1(x=-1,,y=\f(4,3)x,))得eq \b\lc\{(\a\vs4\al\c1(x=-1,,y=-\f(4,3),))由对称性可知公切线l2过点eq \b\lc\(\rc\)(\a\vs4\al\c1(-1,-\f(4,3))).设公切线l2的方程为y+eq \f(4,3)=k(x+1),则点O(0,0)到l2的距离为1,所以1=eq \f(\b\lc\|\rc\|(\a\vs4\al\c1(k-\f(4,3))),\r(k2+1)),解得k=eq \f(7,24),所以公切线l2的方程为y+eq \f(4,3)=eq \f(7,24)(x+1),即7x-24y-25=0;③还有一条公切线l3与直线l:y=eq \f(4,3)x垂直.设公切线l3的方程为y=-eq \f(3,4)x+t,易知t>0,则点O(0,0)到l3的距离为1,所以1=eq \f(|t|,\r(\b\lc\(\rc\)(\a\vs4\al\c1(-\f(3,4)))\s\up12(2)+(-1)2)),解得t=eq \f(5,4),所以公切线l3的方程为y=-eq \f(3,4)x+eq \f(5,4),即3x+4y-5=0.综上,所求直线方程为x=-1或7x-24y-25=0或3x+4y-5=0.
课时作业
一、单项选择题
1.直线mx-y+2=0与圆x2+y2=9的位置关系是( )
A.相交 B.相切
C.相离 D.无法确定
答案 A
解析 圆x2+y2=9的圆心为(0,0),半径为3,直线mx-y+2=0恒过点A(0,2),而02+22=4<9,所以点A在圆的内部,所以直线mx-y+2=0与圆x2+y2=9相交.故选A.
2.两圆C1:x2+y2+2x-6y-26=0,C2:x2+y2-4x+2y+4=0的位置关系是( )
A.内切 B.外切
C.相交 D.外离
答案 A
解析 由于圆C1的标准方程为(x+1)2+(y-3)2=36,故圆心为C1(-1,3),半径为6;圆C2的标准方程为(x-2)2+(y+1)2=1,故圆心为C2(2,-1),半径为1.因为两圆的圆心距|C1C2|=eq \r((-1-2)2+(3+1)2)=5=6-1,所以两圆内切.
3.(2023·吉林延边州二模)经过P(2,3)向圆x2+y2=4作切线,切线方程为( )
A.5x-12y+26=0
B.13x-12y+10=0
C.5x-12y+26=0或x=2
D.13x-12y+10=0或x=2
答案 C
解析 当切线的斜率不存在时,直线x=2是圆的切线;当切线的斜率存在时,设切线l的方程为y-3=k(x-2),由(0,0)到切线的距离d=eq \f(|2k-3|,\r(k2+1))=2,得k=eq \f(5,12),此时切线方程为y-3=eq \f(5,12)(x-2),即5x-12y+26=0.故选C.
4.(2021·北京高考)已知圆C:x2+y2=4,直线l:y=kx+m,当k变化时,l截得圆C弦长的最小值为2,则m=( )
A.±2 B.±eq \r(2)
C.±eq \r(3) D.±eq \r(5)
答案 C
解析 由题可得圆心为(0,0),半径为2,则圆心到直线的距离d=eq \f(|m|,\r(k2+1)),则弦长为2eq \r(4-\f(m2,k2+1)),则当k=0时,弦长取得最小值为2eq \r(4-m2)=2,解得m=±eq \r(3).故选C.
5.若曲线y=eq \r(4-x2)与直线y=k(x-2)+4有两个交点,则实数k的取值范围是( )
A.eq \b\lc\(\rc\](\a\vs4\al\c1(\f(3,4),1)) B.eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,4),+∞))
C.(1,+∞) D.(1,3]
答案 A
解析 根据题意画出图形,如图所示.由题意可得,曲线y=eq \r(4-x2)的图象为以(0,0)为圆心,2为半径的半圆,直线l恒过A(2,4),当直线l与半圆相切时,圆心到直线l的距离d=r,即eq \f(|4-2k|,\r(1+k2))=2,解得k=eq \f(3,4);当直线l过点B时,直线l的斜率k=eq \f(4-0,2-(-2))=1,则直线l与半圆有两个不同的交点时,实数k的取值范围为eq \b\lc\(\rc\](\a\vs4\al\c1(\f(3,4),1)).故选A.
6.(2023·北京东城区模拟)设A是圆C:(x+1)2+y2=9上的动点,PA是圆的切线,且|PA|=4,则点P到点Q(5,8)距离的最小值为( )
A.4 B.5
C.6 D.15
答案 B
解析 由圆C:(x+1)2+y2=9,可知圆心C(-1,0),半径为3,又|PA|=4,所以|PC|2=|PA|2+32=25,设P(x,y),则点P的轨迹方程为(x+1)2+y2=25,故点P到点Q(5,8)距离的最小值为eq \r((5+1)2+82)-5=5.故选B.
7.(2023·新课标Ⅰ卷)过点(0,-2)与圆x2+y2-4x-1=0相切的两条直线的夹角为α,则sinα=( )
A.1 B.eq \f(\r(15),4)
C.eq \f(\r(10),4) D.eq \f(\r(6),4)
答案 B
解析 解法一:因为x2+y2-4x-1=0,即(x-2)2+y2=5,可得圆心C(2,0),半径r=eq \r(5),过点P(0,-2)作圆C的切线,切点为A,B,因为|PC|=eq \r(22+(-2)2)=2eq \r(2),则|PA|=eq \r(|PC|2-r2)=eq \r(3),可得sin∠APC=eq \f(\r(5),2\r(2))=eq \f(\r(10),4),cs∠APC=eq \f(\r(3),2\r(2))=eq \f(\r(6),4),则sin∠APB=sin(2∠APC)=2sin∠APCcs∠APC=2×eq \f(\r(10),4)×eq \f(\r(6),4)=eq \f(\r(15),4),cs∠APB=cs(2∠APC)=cs2∠APC-sin2∠APC=eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(6),4)))eq \s\up12(2)-eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(10),4)))eq \s\up12(2)=-eq \f(1,4)<0,即∠APB为钝角,所以sinα=sin(π-∠APB)=sin∠APB=eq \f(\r(15),4).故选B.
解法二:圆x2+y2-4x-1=0的圆心C(2,0),半径r=eq \r(5),过点P(0,-2)作圆C的切线,切点为A,B,连接AB,可得|PC|=eq \r(22+(-2)2)=2eq \r(2),则|PA|=|PB|=eq \r(|PC|2-r2)=eq \r(3),因为|PA|2+|PB|2-2|PA|·|PB|cs∠APB=|CA|2+|CB|2-2|CA|·|CB|cs∠ACB,且∠ACB=π-∠APB,则3+3-6cs∠APB=5+5-10cs(π-∠APB),即3-3cs∠APB=5+5cs∠APB,解得cs∠APB=-eq \f(1,4)<0,即∠APB为钝角,则csα=cs(π-∠APB)=-cs∠APB=eq \f(1,4),又α为锐角,所以sinα=eq \r(1-cs2α)=eq \f(\r(15),4).故选B.
解法三:圆x2+y2-4x-1=0的圆心C(2,0),半径r=eq \r(5),若切线斜率不存在,则切线方程为x=0,则圆心到切线的距离d=2
8.已知⊙M:x2+y2-2x-2y-2=0,直线l:2x+y+2=0,P为l上的动点,过点P作⊙M的切线PA,PB,切点为A,B,当|PM|·|AB|最小时,直线AB的方程为( )
A.2x-y-1=0 B.2x+y-1=0
C.2x-y+1=0 D.2x+y+1=0
答案 D
解析 圆M的方程可化为(x-1)2+(y-1)2=4,则M(1,1),点M到直线l的距离为d=eq \f(|2×1+1+2|,\r(22+12))=eq \r(5)>2,所以直线l与圆M相离.依圆的知识可知,点A,P,B,M四点共圆,且AB⊥PM,所以|PM|·|AB|=4S△PAM=4×eq \f(1,2)|PA|×|AM|=4|PA|,而|PA|=eq \r(|PM|2-|AM|2)=eq \r(|PM|2-4),当直线l⊥PM时,|PM|最小,|PM|min=eq \r(5),|PA|min=1,此时|PM|·|AB|最小.直线PM的方程为y-1=eq \f(1,2)(x-1),即y=eq \f(1,2)x+eq \f(1,2),由eq \b\lc\{(\a\vs4\al\c1(y=\f(1,2)x+\f(1,2),,2x+y+2=0,))解得eq \b\lc\{(\a\vs4\al\c1(x=-1,,y=0,))所以P(-1,0).所以以PM为直径的圆的方程为(x-1)(x+1)+y(y-1)=0,即x2+y2-y-1=0.两圆的方程相减可得2x+y+1=0,即为直线AB的方程.故选D.
二、多项选择题
9.(2023·黄冈模拟)已知圆C:(x+1)2+y2=9,则下列四个命题表述正确的是( )
A.圆C上有且仅有3个点到直线l:x-eq \r(3)y-1=0的距离等于1
B.过点A(3,4)作圆C的两条切线,切点分别为M,N,直线MN的方程为4x+4y-5=0
C.一条直线与圆C交于不同的两点P,Q,且有eq \r(3)|eq \(CP,\s\up6(→))+eq \(CQ,\s\up6(→))|-|eq \(PQ,\s\up6(→))|≥0,则∠PCQ的最大值为eq \f(2π,3)
D.若圆C与圆E:x2+y2-4x-8y+m2=0相外切,则m=4
答案 BC
解析 圆心C(-1,0),半径r=3,圆心C到直线l:x-eq \r(3)y-1=0的距离d=eq \f(|-1-\r(3)×0-1|,\r(12+(-\r(3))2))=1,故圆C上有4个点到直线l的距离为1,故A错误;过点A(3,4)作圆C的两条切线,切点分别为M,N,则A,C,M,N四点共圆,且AC为直径,方程为x2+y2-2x-4y-3=0,与圆C的方程相减可得,直线MN的方程为4x+4y-5=0,故B正确;设PQ的中点为D,则CD⊥PQ.因为eq \r(3)|eq \(CP,\s\up6(→))+eq \(CQ,\s\up6(→))|-|eq \(PQ,\s\up6(→))|≥0,即eq \r(3)·2|eq \(CD,\s\up6(→))|≥2|eq \(PD,\s\up6(→))|,可得eq \r(3)≥eq \f(|\(PD,\s\up6(→))|,|\a\vs4\al(\(CD,\s\up6(→)))|)=tan∠DCP,则0<∠DCP≤eq \f(π,3),故∠PCQ的最大值为eq \f(2π,3),故C正确;圆E:x2+y2-4x-8y+m2=0的圆心为E(2,4),半径R=eq \r(20-m2),根据题意可得R+r=|CE|,即3+eq \r(20-m2)=5,解得m=±4,故D错误.故选BC.
10.(2024·合肥二模)若圆C1:x2+y2=4与圆C2:(x-m)2+(y-n)2=4的公共弦AB的长为2eq \r(3),则下列结论正确的是( )
A.m2+n2=4
B.直线AB的方程为mx+ny-2=0
C.AB中点的轨迹方程为x2+y2=3
D.四边形AC1BC2的面积为eq \r(3)
答案 AB
解析 对于A,圆C1:x2+y2=4与圆C2:(x-m)2+(y-n)2=4,两圆的方程相减可得2mx+2ny-m2-n2=0,即两圆公共弦的方程为2mx+2ny-m2-n2=0,圆C1:x2+y2=4的圆心为(0,0),半径R=2,圆心C1到直线2mx+2ny-m2-n2=0的距离d=eq \f(|m2+n2|,2\r(m2+n2))=eq \f(\r(m2+n2),2),而两个圆的公共弦AB的长为2eq \r(3),则eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2\r(3),2)))eq \s\up12(2)=4-eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(m2+n2),2)))eq \s\up12(2),即m2+n2=4,A正确;对于B,由于两圆公共弦AB的方程为2mx+2ny-m2-n2=0,且m2+n2=4,故两圆公共弦AB的方程为2mx+2ny-4=0,即mx+ny-2=0,B正确;对于C,设AB的中点坐标为(x,y),由于C1C2垂直平分AB,则C1到AB中点的距离就是C1到直线AB的距离,则x2+y2=1,即AB中点的轨迹方程为x2+y2=1,C错误;对于D,两圆的半径相等,则四边形AC1BC2为菱形,其面积S=2×eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)×1×2\r(3)))=2eq \r(3),D错误.故选AB.
11.(2021·新高考Ⅰ卷)已知点P在圆(x-5)2+(y-5)2=16上,点A(4,0),B(0,2),则( )
A.点P到直线AB的距离小于10
B.点P到直线AB的距离大于2
C.当∠PBA最小时,|PB|=3eq \r(2)
D.当∠PBA最大时,|PB|=3eq \r(2)
答案 ACD
解析 设圆(x-5)2+(y-5)2=16的圆心为M(5,5),由题易知直线AB的方程为eq \f(x,4)+eq \f(y,2)=1,即x+2y-4=0,则圆心M到直线AB的距离d=eq \f(|5+2×5-4|,\r(5))=eq \f(11,\r(5))>4,所以直线AB与圆M相离,所以点P到直线AB的距离的最大值为4+d=4+eq \f(11,\r(5)),4+eq \f(11,\r(5))<5+eq \r(\f(125,5))=10,故A正确;易知点P到直线AB的距离的最小值为d-4=eq \f(11,\r(5))-4,eq \f(11,\r(5))-4
12.圆心在直线y=-4x上,并且与直线l:x+y-1=0相切于点P(3,-2)的圆的方程为________.
答案 (x-1)2+(y+4)2=8
解析 设圆心A的坐标为(a,-4a),则kAP=eq \f(2-4a,a-3),又圆A与直线l相切,∴kAP·kl=-1,又kl=-1,∴a=1,∴A(1,-4),r=eq \r((1-3)2+(-4+2)2)=2eq \r(2),∴所求圆的方程为(x-1)2+(y+4)2=8.
13.(2023·广东东莞期中)一条光线从点(-2,-3)射出,经y轴反射后与圆(x+3)2+(y-2)2=1相切,则反射光线所在直线的斜率为________.
答案 -eq \f(3,4)或-eq \f(4,3)
解析 圆(x+3)2+(y-2)2=1的圆心为(-3,2),半径为1,根据光的反射原理知,反射光线的反向延长线必过点(-2,-3)关于y轴的对称点(2,-3),易知反射光线所在直线的斜率存在,设为k,则反射光线所在直线的方程为y+3=k(x-2),即kx-y-2k-3=0,由反射光线与圆(x+3)2+(y-2)2=1相切,可得eq \f(|-3k-2-2k-3|,\r(k2+1))=1,整理得12k2+25k+12=0,解得k=-eq \f(4,3)或k=-eq \f(3,4).
14.在平面直角坐标系中,已知点A(-1,0),B(2,0),圆C:(x-2)2+(y-m)2=eq \f(1,4)(m>0),在圆上存在点P满足|PA|=2|PB|,则实数m的取值范围是________.
答案 eq \b\lc\[\rc\](\a\vs4\al\c1(\f(\r(5),2),\f(\r(21),2)))
解析 设点P(x,y),由|PA|=2|PB|可得(x+1)2+y2=4[(x-2)2+y2],化简得(x-3)2+y2=4,即点P的轨迹是圆心为Q(3,0),半径为r=2的圆,因为点P在圆C:(x-2)2+(y-m)2=eq \f(1,4)(m>0)上,所以圆Q和圆C有公共点,所以eq \b\lc\|\rc\|(\a\vs4\al\c1(2-\f(1,2)))≤|QC|≤eq \b\lc\|\rc\|(\a\vs4\al\c1(2+\f(1,2))),故eq \f(3,2)≤eq \r(1+m2)≤eq \f(5,2),即eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,2)))eq \s\up12(2)≤1+m2≤eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(5,2)))eq \s\up12(2),所以eq \f(5,4)≤m2≤eq \f(21,4),又m>0,所以eq \f(\r(5),2)≤m≤eq \f(\r(21),2).
四、解答题
15.(2023·赣州模拟)已知在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4.圆C的半径为1,圆心C在直线l上.
(1)若直线3x+4y-12=0与圆C相切,求圆C的标准方程;
(2)已知动点M(x,y),满足|MA|=2|MO|,说明M的轨迹是什么?若点M同时在圆C上,求圆心C的横坐标a的取值范围.
解 (1)因为圆心C在直线l上,所以圆心C可设为(a,2a-4),
由题意可得eq \f(|3a+4(2a-4)-12|,\r(32+42))=eq \f(|11a-28|,5)=1,即|11a-28|=5,
由11a-28=±5,解得a=3或a=eq \f(23,11),
圆心C的坐标为(3,2)或eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(23,11),\f(2,11))),
所以圆C的标准方程为(x-3)2+(y-2)2=1或eq \b\lc\(\rc\)(\a\vs4\al\c1(x-\f(23,11)))eq \s\up12(2)+eq \b\lc\(\rc\)(\a\vs4\al\c1(y-\f(2,11)))eq \s\up12(2)=1.
(2)由|MA|=2|MO|,得eq \r(x2+(y-3)2)=2eq \r(x2+y2),
化简得x2+y2+2y-3=0,即x2+(y+1)2=4,
所以动点M的轨迹是以D(0,-1)为圆心,2为半径的圆,
若点M同时在圆C上,则圆C与圆D有公共点,
则2-1≤|CD|≤2+1,即1≤eq \r(a2+(2a-3)2)≤3,
整理得eq \b\lc\{(\a\vs4\al\c1(5a2-12a+8≥0,,5a2-12a≤0,))解得0≤a≤eq \f(12,5),
所以圆心C的横坐标a的取值范围为eq \b\lc\[\rc\](\a\vs4\al\c1(0,\f(12,5))).
16.已知直线l:4x+3y+10=0,半径为2的圆C与l相切,圆心C在x轴上且在直线l的右上方.
(1)求圆C的方程;
(2)过点M(1,0)的直线与圆C交于A,B两点(A在x轴上方),问在x轴正半轴上是否存在定点N,使得x轴平分∠ANB?若存在,求出点N的坐标;若不存在,请说明理由.
解 (1)设圆心C(a,0)eq \b\lc\(\rc\)(\a\vs4\al\c1(a>-\f(5,2))),
则eq \f(|4a+10|,5)=2⇒a=0或a=-5(舍去).
所以圆C的方程为x2+y2=4.
(2)当直线AB的斜率不存在时,x轴平分∠ANB.
当直线AB的斜率存在时,设直线AB的方程为y=k(x-1),N(t,0),A(x1,y1),B(x2,y2),
由eq \b\lc\{(\a\vs4\al\c1(x2+y2=4,,y=k(x-1),))得(k2+1)x2-2k2x+k2-4=0,
所以x1+x2=eq \f(2k2,k2+1),x1x2=eq \f(k2-4,k2+1).
若x轴平分∠ANB,
则kAN=-kBN⇒eq \f(y1,x1-t)+eq \f(y2,x2-t)=0⇒eq \f(k(x1-1),x1-t)+eq \f(k(x2-1),x2-t)=0⇒2x1x2-(t+1)(x1+x2)+2t=0⇒eq \f(2(k2-4),k2+1)-eq \f(2k2(t+1),k2+1)+2t=0⇒t=4,
所以当点N的坐标为(4,0)时,能使得∠ANM=∠BNM总成立.方法
过程
依据
结论
代数法
联立方程组消去x(或y)得一元二次方程,计算Δ=b2-4ac
Δ>0
eq \x(\s\up1(01))相交
Δ=0
eq \x(\s\up1(02))相切
Δ<0
eq \x(\s\up1(03))相离
几何法
计算圆心到直线的距离d,比较d与半径r的关系
deq \x(\s\up1(04))<r
相交
deq \x(\s\up1(05))=r
相切
deq \x(\s\up1(06))>r
相离
位置关系
图示
d与r1,r2的关系
外离
eq \x(\s\up1(07))d>r1+r2
外切
eq \x(\s\up1(08))d=r1+r2
相交
eq \x(\s\up1(09))|r1-r2|<d<r1+r2
内切
d=eq \x(\s\up1(10))|r1-r2|(r1≠r2)
内含
0≤d<eq \x(\s\up1(11))|r1-r2|(r1≠r2)
考向一 直线与圆的位置关系
几何法
利用d与r的关系判断
代数法
联立方程之后利用Δ判断
点与圆的位置关系法
若直线恒过定点且定点在圆内,可判断直线与圆相交
考向二 直线与圆的综合问题
几何法
直线被圆截得的半弦长eq \f(l,2)、弦心距d和圆的半径r构成直角三角形,且r2=eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(l,2)))eq \s\up12(2)+d2
代数法
将直线和圆的方程联立方程组,消元后得到一个一元二次方程.在判别式Δ>0的前提下,利用根与系数的关系求弦长.弦长公式如下:
|AB|=eq \r(1+k2)·eq \r((x1+x2)2-4x1x2)或|AB|=eq \r(1+\f(1,k2))·eq \r((y1+y2)2-4y1y2)(k≠0)
考向三 两圆的位置关系
高考数学科学创新复习方案提升版第51讲双曲线(一)学案(Word版附解析): 这是一份高考数学科学创新复习方案提升版第51讲双曲线(一)学案(Word版附解析),共22页。
高考数学科学创新复习方案提升版第52讲双曲线(二)学案(Word版附解析): 这是一份高考数学科学创新复习方案提升版第52讲双曲线(二)学案(Word版附解析),共26页。
高考数学科学创新复习方案提升版第53讲抛物线(一)学案(Word版附解析): 这是一份高考数学科学创新复习方案提升版第53讲抛物线(一)学案(Word版附解析),共17页。












