





中职高教版(2021)第4章 立体几何4.1 平面精品ppt课件
展开我们知道,构成空间的基本要素是点、线、面,在平面几何中,我们学习的重点是点与直线,下面我们先重点学习平面.
4.1.1 平面的特征和表示
茶卡盐湖被称为“中国的天空之镇”,当其湖面平静之时就像一面镜子,给人很“平”的印象.面对浩瀚的大海时,我们会感慨大海“一望无际”.茶卡盐湖湖面和海面都可以用“平面”来描述.类似地,课桌桌面、书本封面也可以用“平面”来描述.这些平面有什么共同特征呢?
这些面都是平的,可以向各个方向无限延展.数学中的平面具有平和无限延展的特征.
数学中,因直线具有无限延伸性,所以人们作直线时实际只画出直线的一部分来表示整条直线. 类似地,我们用平面的一部分来表示平面.通常我们用平行四边形三角形、圆等平面图形来表示平面.
怎样画出具有无限延展性的平面呢?
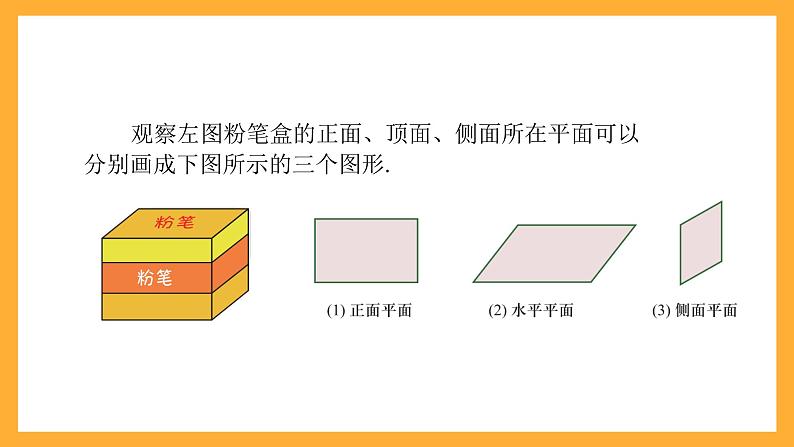
观察左图粉笔盒的正面、顶面、侧面所在平面可以分别画成下图所示的三个图形.
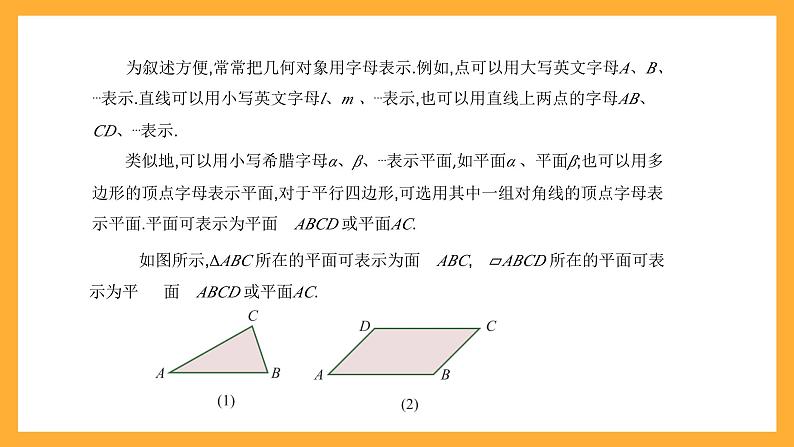
为叙述方便,常常把几何对象用字母表示.例如,点可以用大写英文字母A、B、⋯表示.直线可以用小写英文字母l、m 、⋯表示,也可以用直线上两点的字母AB、CD、⋯表示.
类似地,可以用小写希腊字母α、β、⋯表示平面,如平面α 、平面β;也可以用多边形的顶点字母表示平面,对于平行四边形,可选用其中一组对角线的顶点字母表示平面.平面可表示为平面 ABCD 或平面AC.
如图所示,ΔABC 所在的平面可表示为面 ABC, ⏥ABCD 所在的平面可表示为平 面 ABCD 或平面AC.
考虑到直线和平面均可看作由无数个点组成的点集,当点P在直线l或平面α内时,可分别表示为P∈l, P∈α.当点P不在直线l或不在平面α内时,可分别表为P∉l, P∉α.
典例1 用符号语言表示以下点与直线,平面的位置关系,并画出满足条件的一个图形.(1)点A在直线l上,且在平面α内.(2)点C 不在平面β内,直线m经过点C且与平面β有一个公共点B.
解:(1) A∈l且 A∈α,如图所示.画法:①画平行四边形表示平面α;②将点A画在平行四边形的内部;③经过点A画直线l.
典例1 用符号语言表示以下点与直线,平面的位置关系,并画出满足条件的一个图形.(2)点C 不在平面β内,直线m经过点C且与平面β有一个公共点B.
解: ( 2) C ∉ β,C∈m,B∈m, B∈ β ,如图所示.画法:①画平行四边形表示平面β ;②将点C画在平行四边形的外部;③将点B画在平行四边形内;④连接点C与点B并向两个方向延长,将直线CB标注为直线m,并将直线被平面遮挡部分擦除或画为虚线.
画直线与平面相交时,直线被平面遮挡的部分画出虚线或不画.
【巩固】表示出正方体 (如图)的6个面.
1. 判断下列说法是否正确. (1)平整的课桌面是一个平面的一部分; (2)不同平面的大小是不同的: (3)光滑的玻璃球的表面是一个平面; (4)长方体 ABCD-A1B1C1D1中,四边形ABB1A1,所在平面可表示为平面AB1; (5)把一块长为3m、宽为1.5m 的黑板看作一个平面,这个平面的面积是 4.5 m.
2.已知ABCD-A1B1C1D1,如图所示.试用符号“∈”或“∉”填空. A 直线 AD, A 直线 A1B1 , A 平面BD, A 平面BC1.
3. 请画出符合下列条件的一个图形. (1) A ∉ l, A∈α; (2) B ∉ l, B ∉ β. 4. 观察自己身边有哪些事物可以看作平面的一部分.
4.1.2平面的基本性质
如图所示,分别尝试用一个指尖、两个指尖、三个指尖顶起一块硬纸板,看看哪种方式能比较稳地将硬纸板顶起来?
你有什么发现?
尝试后发现,当三个指尖不在同一条直线上时,能将硬纸板平稳地顶起来.
这个现象蕴含着平面的如下重要性质.
公理1 经过不在同一条直线上的三点,有且只有一个平面.
这个公理也可以说成“不共线的三点确定一个平面”.
如图所示,点A、B、C不共线.由公理 1可知,存在唯一的平面α,使得A∈α, B∈α, C∈α.
容易看出,经过一个点、两个点或共线的三个点有无数个平面,也可以说成“一个点,两个点或共线的三个点不能确定一个平面”.
将一根细线拉直,然后把它的两个端点固定在桌面上,如图所示,观察细线上其他的点与桌面的关系.如果抓住细线中的一点并拉离桌面,细线还是直线吗?
容易看出,当把拉直的细线的两个端点放在桌面上时,细线上的所有点都在桌面上.
如果将细线抽象为直线,桌面抽象成平面,可以得出平面的如下性质.
公理2 如果一条直线上的两个点在一个平面内,那么这条直线上的所有点都在这个平面内.有且只有一个平面.
当一条直线上的所有点都在平面内时,称直线在平面内,或者说平面经过直线.
如图所示,由A∈α, B∈α,可知AB⊆α .
因为直线和平面都是由点组成的集合,所以直线m在平面α内可表示为m⊆α .当直线m不在平面α内时,表示为 m⊈α ,此时直线与平面有一个公共点或没有公共点.
表示直线在平面内时,要把直线画在表示平面的图形的内部.
由公理1、2得到以下结论.
推论1 经过一条直线和该直线外的一点有且只有一个平面.
如图所示,A∈l,存在唯一的平面α,使得A∈α,l⊆α.
推论2 经过两条相交直线有且只有一个平面.
如图所示,直线m与直线n相较于点A,存在唯一的平面α,使得m⊆α,n⊆α.
推论3 经过两条平行直线有且只有一个平面.
如图所示, m∥n,存在唯一的平面α,使得m⊆α,n⊆α.
将一块薄的硬纸板平放到桌面上,可视作硬纸板和桌面所在的平面重合,如图所示.抬起硬纸板的一端,让另一端紧贴桌面,则硬纸板和桌面所在台面有一条公共直线.继续抬起硬纸板,将纸板的一角支在桌面上,则支点就是硬纸板和桌面所在平面的一个公共点.这时,它们所在的平面就只有这一个公共点么?
画两个平面相交时,一定要画出它们的交线,平面被遮挡部分用虚线表示或者不画.
典例2试用符号语言表示下列语句,并画出相应的图形. (1)点A、B在直线l上,直线l 在平面α内.
(1) A、B ∈l, l ⊆α,如图所示.画法:①画平行四边形表示平面α;②在平行四边形内画点A、B ;③连接A、B并延长,在直线AB上标出直线l.
典例2试用符号语言表示下列语句,并画出相应的图形. (2)平面α和平面β相交于直线l.
(2) α⋂β=l,如左图所示.画法:①画线段 AB表示交线l,如右图所示;②过点A画与l不同的两条相交线段CD、EF,再过点B画 C'D'与E'F' ,使C'D'∥CD、E'F'∥EF , C'D'=CD,E'F'=EF;③连接 CC' 、DD'、EE'、FF',分别将平面 CD'和平面EF'标注为平面α和平面β,再将被遮挡部分改为虚线或不画,最后擦去字母A、B、C、D、A'、B'、C'、D'.
典例3判断下列说法是否正确. (1)经过三个点有且只有一个平面; (2)如果直线l与平面α有三个公共点,那么l ⊆α; (3)用三角板的一个顶点与桌面接触,只有一个公共点,故两个平面可以只有一个公共点.
(1)错误.经过不共线的三点有且只有一个平面.当三点共线时,经过这三个点有无数个平面;
(2)正确.当一条直线有两个点在平面内时,这条直线就在平面内;
(3)错误.当两个平面有一个公共点时,这两个平面就有一条经过该点的公共直线,因此它们一定有无数个公共点.
典例4在正方体ABCD-A1B1C1D1[图(1)]中,找出符合下列条件的平面. (1)经过点A1、B、D的平面;
(1)经过点A1、B、D的平面是平面A1BD,如图(2)所示;
典例4在正方体ABCD-A1B1C1D1[图(1)]中,找出符合下列条件的平面. (2)经过直线BC和点D1的平面;
(2)经过直线BC和点D1平面是平面BCD1,如图(3)所示;
典例4在正方体ABCD-A1B1C1D1[图(1)]中,找出符合下列条件的平面. (3)经过直线BD和DD1的平面;
(3)经过直线BD和DD1的平面是平面BDD1,如图(4)所示;
典例4在正方体ABCD-A1B1C1D1[图(1)]中,找出符合下列条件的平面. (4)经过直线AB和C1D1的平面;
(4)经过直线AB和C1D1的平面是平面ABC1D1,如图(5)所示.
【巩固】用符号语言表示下列语句,并画出图形.(1)三个平面α、β、γ相交于一点P,且平面α与平面β交于PA,平面α与平面γ交于PB,平面β与平面γ交于PC;(2)平面ABD与平面BCD交于BD,平面ABC与平面ADC交于AC.
[解析] (1)符号语言表示:α∩β∩γ=P,α∩β=PA,α∩γ=PB,β∩γ=PC.图形表示:如图1所示.(2)符号语言表示:平面ABD∩平面BCD=BD,平面ABC∩平面ADC=AC.图形表示:如图2所示.
1.判断下列说法是否正确. (1)经过直线m和点A的平面有且只有一个;(2)两条相交直线可以确定一个平面; (3)同时经过两条平行直线的平面不止一个; (4)两个平面可以只有一条公共线段.
2. 根据平面的基本性质和推论证明平行四边形是平面图形(填空). 已知:四边形 ABCD 是一个平行四边形.求证:AB、BC、CD、DA 四条边共面. 证明:因为 AB∥CD,所以 AB 和CD 确定平面α,如图所示. 因为A∈AB,B∈AB,C∈CD,D∈CD,所以A、B、C、D均在平面α内.从而,有AD⊆ ,BC⊆ , AB⊆ , CD⊆ .所以,AB、BC、CD、DA四条边共面.
3.试用12根长短相等的小木棍(或铁丝等) 制作正方体模型 ABCD-A1B1C1D1, 并指出由顶点A和棱CC1所确定的平面.
(1) 读书部分: 教材章节4.1; (2) 书面作业: P107习题4.1的1,2,3,4,5.
数学是一种别具匠心的艺术
中职数学高教版(2021)拓展模块一 上册3.1.2 椭圆的几何性质优质ppt课件: 这是一份中职数学高教版(2021)拓展模块一 上册<a href="/sx/tb_c4035782_t3/?tag_id=26" target="_blank">3.1.2 椭圆的几何性质优质ppt课件</a>,共23页。PPT课件主要包含了学习目标,创设情境生成问题,调动思维探究新知,对称性,离心率,探究与发现,巩固知识典例练习,温馨提示,巩固练习提升素养,课堂小结等内容,欢迎下载使用。
数学3.1.1 椭圆的标准方程完美版课件ppt: 这是一份数学<a href="/sx/tb_c4035781_t3/?tag_id=26" target="_blank">3.1.1 椭圆的标准方程完美版课件ppt</a>,共24页。PPT课件主要包含了学习目标,创设情境生成问题,调动思维探究新知,巩固知识典例练习,巩固练习提升素养,课堂小结,作业布置等内容,欢迎下载使用。
中职数学高教版(2021)拓展模块一 上册第2章 平面向量2.3 向量的内积优秀课件ppt: 这是一份中职数学高教版(2021)拓展模块一 上册<a href="/sx/tb_c4035773_t3/?tag_id=26" target="_blank">第2章 平面向量2.3 向量的内积优秀课件ppt</a>,共22页。PPT课件主要包含了学习目标,创设情境生成问题,调动思维探究新知,温馨提示,探究与发现,巩固知识典例练习,巩固练习提升素养,课堂小结,作业布置等内容,欢迎下载使用。












