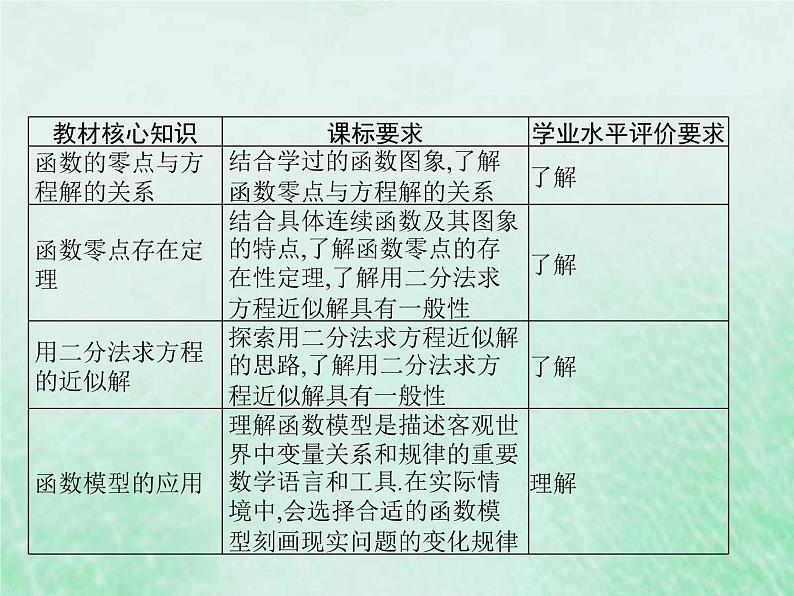
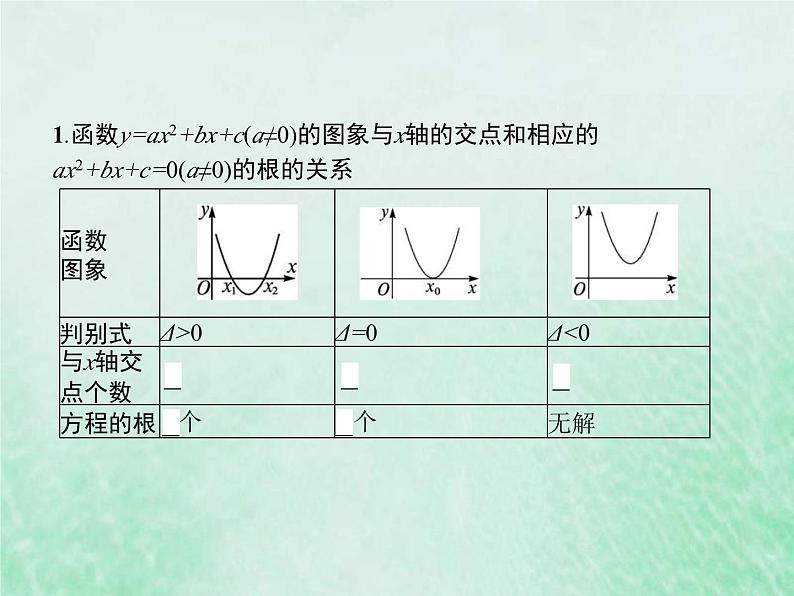
新高考数学一轮复习基础知识综合课件 第8讲 函数的应用（含解析）

这是一份新高考数学一轮复习基础知识综合课件 第8讲 函数的应用（含解析），共14页。PPT课件主要包含了考点一，考点二，考点三，答案C，答案A，答案B等内容，欢迎下载使用。

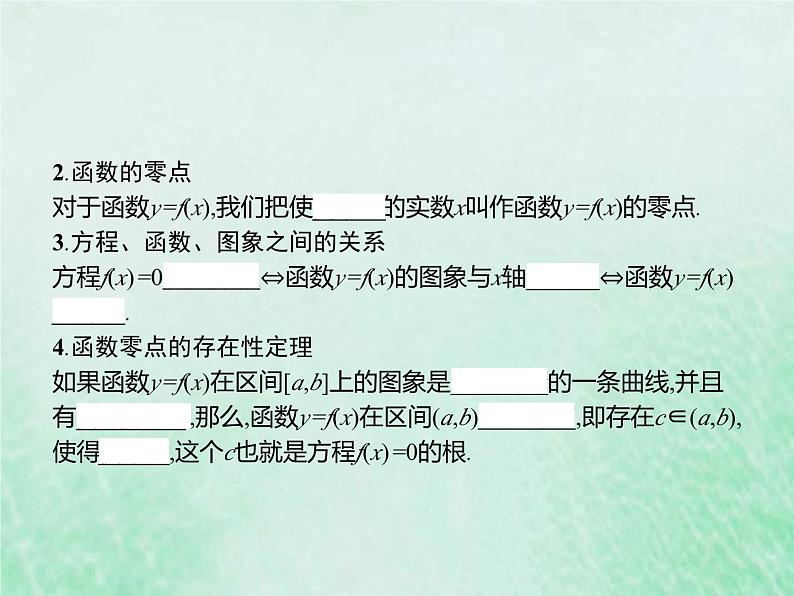
1.函数y=ax2+bx+c(a≠0)的图象与x轴的交点和相应的ax2+bx+c=0(a≠0)的根的关系
2.函数的零点对于函数y=f(x),我们把使 f(x)=0的实数x叫作函数y=f(x)的零点.3.方程、函数、图象之间的关系方程f(x)=0有实数根⇔函数y=f(x)的图象与x轴有交点⇔函数y=f(x)有零点.4.函数零点的存在性定理如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有 f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得 f(c)=0,这个c也就是方程f(x)=0的根.
5.二分法的概念(1)对于在区间[a,b]上连续不断且 f(a)·f(b)<0的函数y=f(x),通过不断地把函数y=f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫作二分法.(2)用二分法求函数y=f(x)零点近似值的步骤:①确定区间[a,b],验证 f(a)·f(b)<0,给定精确度ε;②求区间(a,b)的中点 c ;③计算f(c);i.若f(c)=0,则 c就是函数的零点;ii.若f(a)·f(c)<0,则此时零点x0∈(a,c);iii.若f(b)·f(c)<0,则此时零点x0∈(c,b).
函数的零点◆角度1.零点区间判断例1函数f(x)=ln x+x3-9的零点所在的区间为(　　)A.(0,1)B.(1,2)C.(2,3)D.(3,4)
答案 C　解析 可以求得f(1)=-8<0,f(2)=ln 2-1<0,f(3)=ln 3+18>0,所以函数的零点在区间(2,3)内.故选C.
◆角度2.零点个数判断例2-1函数 的零点个数为(　　)A.0B.1C.2D.3
解析 令y=0,则 =0,即-x2+x+5=0,又Δ=1+20>0,故该方程有两根,且均满足函数定义域内.故该函数有两个零点.故选C.
例2-2方程ln x+x=0的实数解的个数为(　　)A.1B.2C.3D.0
解析 方程ln x+x=0的实数解的个数,即为方程ln x=-x的实数解的个数,即为函数y=ln x与函数y=-x图象的交点的个数,在同一坐标系中作出函数y=ln x与函数y=-x的图象(图略),只有一个交点,所以方程ln x+x=0的实数解的个数为1.故选A.
◆角度3.根据零点求参数例3已知关于x的方程|2x-m|=1有两个不等实根,则实数m的取值范围是(　　)A.(-∞,-1]B.(-∞,-1)C.[1,+∞)D.(1,+∞)
答案 D　解析 由题知m≤0时2x-m>0且y=|2x-m|,即y=2x-m为增函数,所以|2x-m|=1不可能有两个实数根,排除A,B,所以m>0.得m>1,故选D.
二分法例4-1(2020福建高一期中)设f(x)=3x+3x-8,用二分法求方程3x+3x-8=0在x∈(1,2)内近似解的过程中得f(1)<0,f(1.5)>0,f(1.25)<0,则方程的根落在区间(　　)A.(1,1.25)B.(1.25,1.5)C.(1.5,2)D.不能确定
解析 ∵f(x)=3x+3x-8,又f(1.5)>0,f(1.25)<0,∴f(1.5)·f(1.25)<0.由零点存在定理可得f(x)在区间(1.25,1.5)存在零点.∴3x+3x-8=0方程的根落在区间(1.25,1.5).故选B.
例4-2下列函数图象与x轴均有公共点,其中能用二分法求零点的是(　　)
解析 能用二分法求零点的函数必须在给定区间[a,b]上连续不断,并且有f(a)·f(b)<0,A,B中不存在f(x)<0,D中函数不连续.故选C.
函数模型例5某科技股份有限公司为激励创新,计划逐年增加研发资金投入.若该公司2021年全年投入的研发资金为100万元,在此基础上,每年投入的研发资金比上一年增长10%,则该公司全年投入的研发资金开始超过200万元的年份是(　　)(参考数据:lg 1.1=0.041,lg 2=0.301)A.2027年B.2028年C.2029年D.2030年