2022-2023学年北京市朝阳外国语学校八年级（上）期中数学试卷【含解析】

这是一份2022-2023学年北京市朝阳外国语学校八年级（上）期中数学试卷【含解析】，共28页。试卷主要包含了填空题，解答题等内容，欢迎下载使用。

1．（3分）第24届冬季奥林匹克运动会，将于2022年02月04日～2022年02月20日在中华人民共和国北京市和张家口市联合举行．在会徽的图案设计中，设计者常常利用对称性进行设计，下列四个图案是历届会徽图案上的一部分图形，其中不是轴对称图形的是（ ）
A．B．
C．D．
2．（3分）用直角三角板，作△ABC的高，下列作法正确的是（ ）
A．B．
C．D．
3．（3分）空调安装在墙上时，一般都会采用如图的方法固定，这种方法应用的几何原理是（ ）
A．两点确定一条直线B．两点之间线段最短
C．三角形的稳定性D．垂线段最短
4．（3分）下列长度的三条线段中，能组成三角形的是（ ）
A．3cm，5cm，8cmB．8cm，8cm，18cm
C．3cm，3cm，5cmD．3cm，4cm，8cm
5．（3分）已知图中的两个三角形全等，则∠1等于（ ）
A．50°B．58°C．60°D．72°
6．（3分）如图，已知AB＝DC，下列条件中，不能判定△ABC≌△DCB的是（ ）
A．AC＝DBB．∠ACB＝∠DBCC．∠ABC＝∠DCBD．∠A＝∠D＝90°
7．（3分）下列运算正确的是（ ）
A．a3+a6＝a9B．a6•a2＝a12
C．（a3）2＝a5D．a4•a2+（a3）2＝2a6
8．（3分）如图的4×4的正方形网格中，有A、B两点，在直线a上求一点P，使PA+PB最短，则点P应选在（ ）
A．C点B．D点C．E点D．F点
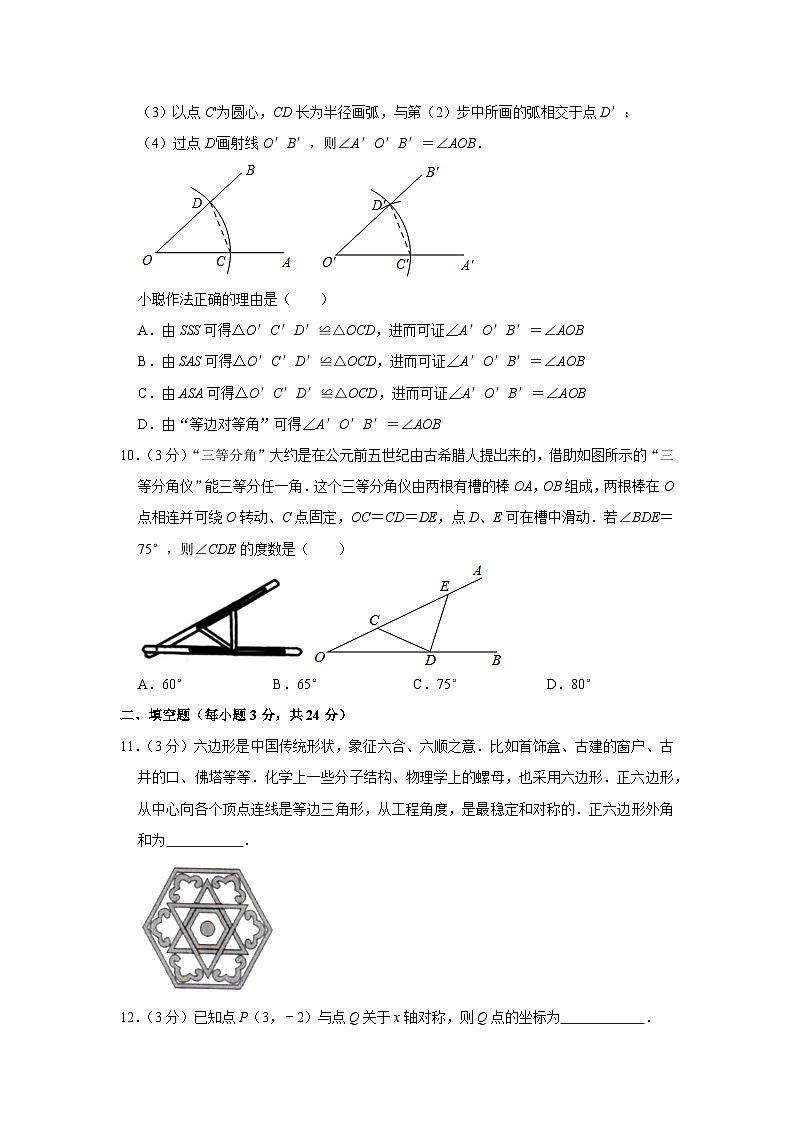
9．（3分）小聪在用直尺和圆规作一个角等于已知角时，具体过程是这样的：
已知：∠AOB．
求作：∠A′O′B′，使∠A′O′B′＝∠AOB．
作法：（1）如图，以点O为圆心，任意长为半径画弧，分别交OA，OB于点C，D；
（2）画一条射线O′A′，以点O′为圆心，OC长为半径画弧，交O′A′于点C′；
（3）以点C'为圆心，CD长为半径画弧，与第（2）步中所画的弧相交于点D′；
（4）过点D'画射线O′B′，则∠A′O′B′＝∠AOB．
小聪作法正确的理由是（ ）
A．由SSS可得△O′C′D′≌△OCD，进而可证∠A′O′B′＝∠AOB
B．由SAS可得△O′C′D′≌△OCD，进而可证∠A′O′B′＝∠AOB
C．由ASA可得△O′C′D′≌△OCD，进而可证∠A′O′B′＝∠AOB
D．由“等边对等角”可得∠A′O′B′＝∠AOB
10．（3分）“三等分角”大约是在公元前五世纪由古希腊人提出来的，借助如图所示的“三等分角仪”能三等分任一角．这个三等分角仪由两根有槽的棒OA，OB组成，两根棒在O点相连并可绕O转动、C点固定，OC＝CD＝DE，点D、E可在槽中滑动．若∠BDE＝75°，则∠CDE的度数是（ ）
A．60°B．65°C．75°D．80°
二、填空题（每小题3分，共24分）
11．（3分）六边形是中国传统形状，象征六合、六顺之意．比如首饰盒、古建的窗户、古井的口、佛塔等等．化学上一些分子结构、物理学上的螺母，也采用六边形．正六边形，从中心向各个顶点连线是等边三角形，从工程角度，是最稳定和对称的．正六边形外角和为 ．
12．（3分）已知点P（3，﹣2）与点Q关于x轴对称，则Q点的坐标为 ．
13．（3分）如图，在一个池塘旁有一条笔直小路（B，C为小路端点）和一棵小树（A为小树位置），测得的相关数据为：∠ABC＝60°，∠ACB＝60°，BC＝58米，则AC＝ 米．
14．（3分）某地地震过后，小娜同学用下面的方法检测教室的房梁是否处于水平：在等腰直角三角尺斜边中点O处拴一条线绳，线绳的另一端挂一个铅锤，把这块三角尺的斜边贴在房梁上，结果线绳经过三角尺的直角顶点，由此得出房梁是水平的即挂铅锤的线绳与房梁直），用到的数学原理是 ．
15．（3分）如图，∠AOE＝∠BOE＝15°，EF∥OB，EC⊥OB，若EC＝2，则EF＝ ．
16．（3分）如图，△ABC中，AB＝AC，AD平分∠BAC，点E是线段BC延长线上一点，连接AE，点C在AE的垂直平分线上，若DE＝12cm，则△ABC的周长是 ．
17．（3分）已知a＝8131，b＝2741，c＝961，则a、b、c的大小关系是 ．
18．（3分）如图，已知四边形ABCD中，AB＝12厘米，BC＝8厘米，CD＝14厘米，∠B＝∠C，点E为线段AB的中点．如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时，点Q在线段CD上由C点向D点运动．当点Q的运动速度为 厘米/秒时，能够使△BPE与以C、P、Q三点所构成的三角形全等．
三、解答题（共46分）
19．（6分）（1）计算：（a4）3+a8•a4；
（2）计算：[（x+y）m+n]2；
（3）已知2x+3y﹣2＝0，求9x•27y的值．
20．（5分）点D为△ABC的边BC的延长线上的一点，DF⊥AB于点F，交AC于点E，∠A＝35°，∠D＝40°，求∠ACD的度数．
21．（5分）已知：如图，C是线段AB的中点，CD＝CE，∠ACE＝∠BCD．求证：AD＝BE．
22．（6分）如图，点B、F、C、E在直线l上（F、C之间不能直接测量），点A、D在l异侧，测得AB＝DE，AB∥DE，∠A＝∠D．
（1）求证：△ABC≌△DEF；
（2）若BE＝10m，BF＝3m，求FC的长度．
23．（5分）如图，已知A（﹣2，3），B（﹣3，1），C（1，﹣2）．
（1）请画出△ABC关于y轴对称的△A'B'C'；（其中A'、B'、C'分别是A，B，C的对应点，不写画法）
（2）A'、B'、C'的坐标分别为 ；
（3）△ABC的面积是 ．
24．（5分）如图，在△ABC中，∠C＝90°，AD平分∠CAB，DE⊥AB于点E，点F在AC上，BD＝DF．求证：BE＝FC．
25．（7分）已知：如图1，AB∥CD，请用尺规作图法，在射线CD上找一点P，使射线AP平分∠BAC．
小明的作图方法如下：
①以点A为圆心，适当长为半径画弧，交AB于点M，交AC于点N；
②分别以点M，N为圆心，大于MN的长为半径画弧，两弧在∠CAB的内部相交于点E；
③画射线AE，交射线CD于点P，点P即为所求．
小刚说：“我有不同的作法，如图2所示，只需要以点C为圆心，CA为半径画弧，交射线CD于点P，画射线AP，也能够得到AP平分∠BAC．
请回答：
（1）请补全小明的作图过程．小明在作图的过程中，构造出一组全等三角形，它们是 ≌ ，全等的依据是 ．因为全等三角形的对应角相等，所以能够得到∠CAB的角平分线AP；
（2）对于小刚的作图方法证明如下：
∵CA＝CP
∴∠CAP＝∠CPA（等边对等角）
∵AB∥CD
∴∠BAP＝∠ （ ）
∴∠CAP＝∠BAP
∴射线AP平分∠BAC．
（3）点P到直线AC和AB的距离相等，理由是 ．
26．（7分）课堂上，老师提出了这样一个问题：
如图1，在△ABC中，AD平分∠BAC交BC于点D，且AB+BD＝AC．
求证：∠ABC＝2∠ACB．
小明的方法是：如图2，在AC上截取AE，使AE＝AB，连接DE，构造全等三角形来证明结论．
（1）小天提出，如果把小明的方法叫做“截长法”，那么还可以用“补短法”通过延长线段AB构造全等三角形进行证明．辅助线的画法是：延长AB至F，使BF＝ ，连接DF．
请补全小天提出的辅助线的画法，并在图1中画出相应的辅助线；
（2）小芸通过探究，将老师所给的问题做了进一步的拓展，给同学们提出了如下的问题：
如图3，点D在△ABC的内部，AD，BD，CD分别平分∠BAC，∠ABC，∠ACB，且AB+BD＝AC．求证：∠ABC＝2∠ACB．
请你解答小芸提出的这个问题；
（3）小东将老师所给问题中的一个条件和结论进行交换，得到的命题如下：
如果在△ABC中，∠ABC＝2∠ACB，点D在边BC上，AB+BD＝AC，那么AD平分∠BAC．
小东判断这个命题也是真命题，老师说小东的判断是正确的．请你利用图4对这个命题进行证明．
2022-2023学年北京市朝阳外国语学校八年级（上）期中数学试卷
参考答案与试题解析
一、选择题（每小题3分，共30分）第1～10题中，每道小题均有四个选项，符合题意的选项只有一个，请将其写在题号前．
1．（3分）第24届冬季奥林匹克运动会，将于2022年02月04日～2022年02月20日在中华人民共和国北京市和张家口市联合举行．在会徽的图案设计中，设计者常常利用对称性进行设计，下列四个图案是历届会徽图案上的一部分图形，其中不是轴对称图形的是（ ）
A．B．
C．D．
【分析】根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．
【解答】解：A、是轴对称图形，故此选项错误；
B、是轴对称图形，故此选项错误；
C、是轴对称图形，故此选项错误；
D、不是轴对称图形，故此选项正确；
故选：D．
【点评】此题主要考查了利用轴对称设计图案，关键是掌握轴对称图形的概念．
2．（3分）用直角三角板，作△ABC的高，下列作法正确的是（ ）
A．B．
C．D．
【分析】根据高线的定义即可得出结论．
【解答】解：A、B、C均不是高线．
故选：D．
【点评】本题考查的是作图﹣基本作图，熟知三角形高线的定义是解答此题的关键．
3．（3分）空调安装在墙上时，一般都会采用如图的方法固定，这种方法应用的几何原理是（ ）
A．两点确定一条直线B．两点之间线段最短
C．三角形的稳定性D．垂线段最短
【分析】钉在墙上的方法是构造三角形支架，因而应用了三角形的稳定性．
【解答】解：这种方法应用的数学知识是：三角形的稳定性，
故选：C．
【点评】本题主要考查了三角形的稳定性，正确掌握三角形的这一性质是解题的关键．
4．（3分）下列长度的三条线段中，能组成三角形的是（ ）
A．3cm，5cm，8cmB．8cm，8cm，18cm
C．3cm，3cm，5cmD．3cm，4cm，8cm
【分析】根据三角形的三边关系“任意两边之和大于第三边，任意两边之差小于第三边”，进行分析．
【解答】解：A.3+5＝8，不能构成三角形，故不符合题意；
B.8+8＝16＜18，不能构成三角形，故不符合题意；
C.3+3＝6＞5，能构成三角形，故符合题意；
D.3+4＝7＜8，不能构成三角形，故不符合题意．
故选：C．
【点评】此题主要考查了三角形三边关系，根据第三边的范围是：大于已知的两边的差，而小于两边的和是解决问题的关键．
5．（3分）已知图中的两个三角形全等，则∠1等于（ ）
A．50°B．58°C．60°D．72°
【分析】根据已知数据找出对应角，根据全等得出∠A＝∠D＝50°，∠F＝∠C＝72°，根据三角形内角和定理求出即可．
【解答】解：
∵△ABC和△DEF全等，AC＝DF＝b，DE＝AB＝a，
∴∠1＝∠B，∠A＝∠D＝50°，∠F＝∠C＝72°，
∴∠1＝180°﹣∠D﹣∠F＝58°，
故选：B．
【点评】本题考查了三角形内角和定理，全等三角形的性质的应用，能根据全等三角形的性质得出∠A＝∠D＝50°，∠F＝∠C＝72°是解此题的关键，注意：全等三角形的对应边相等，对应角相等．
6．（3分）如图，已知AB＝DC，下列条件中，不能判定△ABC≌△DCB的是（ ）
A．AC＝DBB．∠ACB＝∠DBCC．∠ABC＝∠DCBD．∠A＝∠D＝90°
【分析】从图中读取公共边BC＝CB的条件，结合每个选项给出的条件，只要能够判定两个三角形全等的都排除，从而找到不能判定两个三角形全等的选项B．
【解答】解：由题知，AB＝DC，BC＝CB，
当AC＝DB时，△ABC≌△DCB（SSS），故选项A能判定两个三角形全等，所以不选A；
当∠ACB＝∠DBC，不能判定，△ABC≌△DCB，故选B；
当∠ABC＝∠DCB，△ABC≌△DCB（SAS），故选项C能判定两个三角形全等，所以不选C；
当∠A＝∠D＝90°，Rt△ABC≌Rt△DCB（HL），故选项D能判定两个三角形全等，所以不选D．
故选：B．
【点评】本题考查全等三角形的判定，注意一般三角形的“边边角”不能判定两个三角形全等，以及直角三角形的“HL”可以判定两个三角形全等．
7．（3分）下列运算正确的是（ ）
A．a3+a6＝a9B．a6•a2＝a12
C．（a3）2＝a5D．a4•a2+（a3）2＝2a6
【分析】A．应用合并同类项法则进行计算即可得出答案；
B．应用同底数幂乘法法则进行计算即可得出答案；
C．应用幂的乘方法则进行计算即可得出答案；
D．应用幂的乘方与积的乘方，合并同类项及同底数幂乘法进行计算即可得出答案．
【解答】解：A．因为a3与a6不是同类项，故A选项计算不正确，故A选项不符合题意；
B．因为a6•a2＝a6+2＝a8，故B选项计算不正确，故B选项不符合题意；
C．因为（a3）2＝a3×2＝a6，故C选项计算不正确，故C选项不符合题意；
D．因为a4•a2+（a3）2＝a6+a6＝2a6，故D选项计算正确，故D选项符合题意．
故选：D．
【点评】本题主要考查了幂的乘方与积的乘方，合并同类项及同底数幂乘法，熟练掌握幂的乘方与积的乘方，合并同类项及同底数幂乘法法则进行求解是解决本题的关键．
8．（3分）如图的4×4的正方形网格中，有A、B两点，在直线a上求一点P，使PA+PB最短，则点P应选在（ ）
A．C点B．D点C．E点D．F点
【分析】首先求得点A关于直线a的对称点A′，连接A′B，即可求得答案．
【解答】解：如图，点A′是点A关于直线a的对称点，连接A′B，则A′B与直线a的交点，即为点P，此时PA+PB最短，
∵A′B与直线a交于点C，
∴点P应选C点．
故选：A．
【点评】此题考查了最短路径问题．注意首先作出其中一点关于直线L的对称点，对称点与另一点的连线与直线L的交点就是所要找的点．
9．（3分）小聪在用直尺和圆规作一个角等于已知角时，具体过程是这样的：
已知：∠AOB．
求作：∠A′O′B′，使∠A′O′B′＝∠AOB．
作法：（1）如图，以点O为圆心，任意长为半径画弧，分别交OA，OB于点C，D；
（2）画一条射线O′A′，以点O′为圆心，OC长为半径画弧，交O′A′于点C′；
（3）以点C'为圆心，CD长为半径画弧，与第（2）步中所画的弧相交于点D′；
（4）过点D'画射线O′B′，则∠A′O′B′＝∠AOB．
小聪作法正确的理由是（ ）
A．由SSS可得△O′C′D′≌△OCD，进而可证∠A′O′B′＝∠AOB
B．由SAS可得△O′C′D′≌△OCD，进而可证∠A′O′B′＝∠AOB
C．由ASA可得△O′C′D′≌△OCD，进而可证∠A′O′B′＝∠AOB
D．由“等边对等角”可得∠A′O′B′＝∠AOB
【分析】先利用作法得到OD＝OC＝OD′＝OC′，CD＝C′D′，然后根据全等三角形的判定方法对各选项进行判断．
【解答】解：由作图得OD＝OC＝OD′＝OC′，CD＝C′D′，
则根据“SSS”可判断△C′O′D′≌△COD．
故选：A．
【点评】本题考查了作图﹣基本作图：基本作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．也考查了全等三角形的判定．
10．（3分）“三等分角”大约是在公元前五世纪由古希腊人提出来的，借助如图所示的“三等分角仪”能三等分任一角．这个三等分角仪由两根有槽的棒OA，OB组成，两根棒在O点相连并可绕O转动、C点固定，OC＝CD＝DE，点D、E可在槽中滑动．若∠BDE＝75°，则∠CDE的度数是（ ）
A．60°B．65°C．75°D．80°
【分析】根据OC＝CD＝DE，可得∠O＝∠ODC，∠DCE＝∠DEC，根据三角形的外角性质可知∠DCE＝∠O+∠ODC＝2∠ODC，进一步根据三角形的外角性质可知∠BDE＝3∠ODC＝75°，即可求出∠ODC的度数，进而求出∠CDE的度数．
【解答】解：∵OC＝CD＝DE，
∴∠O＝∠ODC，∠DCE＝∠DEC，
∴∠DCE＝∠O+∠ODC＝2∠ODC，
∵∠O+∠OED＝3∠ODC＝∠BDE＝75°，
∴∠ODC＝25°，
∵∠CDE+∠ODC＝180°﹣∠BDE＝105°，
∴∠CDE＝105°﹣∠ODC＝80°．
故选：D．
【点评】本题主要考查了等腰三角形的性质以及三角形的外角性质，理清各个角之间的关系是解答本题的关键．
二、填空题（每小题3分，共24分）
11．（3分）六边形是中国传统形状，象征六合、六顺之意．比如首饰盒、古建的窗户、古井的口、佛塔等等．化学上一些分子结构、物理学上的螺母，也采用六边形．正六边形，从中心向各个顶点连线是等边三角形，从工程角度，是最稳定和对称的．正六边形外角和为 360° ．
【分析】根据任何多边形的外角和是360度即可求出答案．
【解答】解：正六边形的外角和是360°．
故选：360°．
【点评】本题正多边形和圆，考查了多边形的外角和定理，关键是掌握任何多边形的外角和是360度，外角和与多边形的边数无关．
12．（3分）已知点P（3，﹣2）与点Q关于x轴对称，则Q点的坐标为 （3，2） ．
【分析】根据关于x轴对称的点，横坐标相同，纵坐标互为相反数．
【解答】解：根据关于x轴对称的点，横坐标相同，纵坐标互为相反数，
∴点P（3，﹣2）关于x轴对称的点Q为（3，2）．
故答案为：（3，2）．
【点评】本题主要考查了平面直角坐标系内关于x轴对称的点，横坐标相同，纵坐标互为相反数，需要牢记，难度较小．
13．（3分）如图，在一个池塘旁有一条笔直小路（B，C为小路端点）和一棵小树（A为小树位置），测得的相关数据为：∠ABC＝60°，∠ACB＝60°，BC＝58米，则AC＝ 58 米．
【分析】根据等边三角形的判定与性质即可求解．
【解答】解：∵∠ABC＝60°，∠ACB＝60°，
∴∠BAC＝60°，
∴△ABC是等边三角形，
∵BC＝58米，
∴AC＝58米．
故答案为：58．
【点评】考查了等边三角形的判定与性质，关键是得到△ABC是等边三角形．
14．（3分）某地地震过后，小娜同学用下面的方法检测教室的房梁是否处于水平：在等腰直角三角尺斜边中点O处拴一条线绳，线绳的另一端挂一个铅锤，把这块三角尺的斜边贴在房梁上，结果线绳经过三角尺的直角顶点，由此得出房梁是水平的即挂铅锤的线绳与房梁直），用到的数学原理是 等腰三角形的底边上的中线、底边上的高重合 ．
【分析】根据△ABC是个等腰三角形可得AC＝BC，再根据点O是AB的中点，即可得出OC⊥AB，然后即可得出结论．
【解答】解：∵△ABC是个等腰三角形，
∴AC＝BC，
∵点O是AB的中点，
∴AO＝BO，
∴OC⊥AB．
故答案为：等腰三角形的底边上的中线、底边上的高重合．
【点评】本题主要考查了学生对等腰三角形的性质的理解和掌握，此题与实际生活联系密切，体现了从数学走向生活的指导思想，从而达到学以致用的目的．
15．（3分）如图，∠AOE＝∠BOE＝15°，EF∥OB，EC⊥OB，若EC＝2，则EF＝ 4 ．
【分析】作EG⊥OA于F，根据角平分线的性质得到EG的长度，再根据平行线的性质得到∠OEF＝∠COE＝15°，然后利用三角形的外角和内角的关系求出∠EFG＝30°，利用30°角所对的直角边是斜边的一半解题．
【解答】解：作EG⊥OA于G，如图所示：
∵EF∥OB，∠AOE＝∠BOE＝15°
∴∠OEF＝∠COE＝15°，EG＝CE＝2，
∵∠AOE＝15°，
∴∠EFG＝15°+15°＝30°，
∴EF＝2EG＝4．
故答案为：4．
【点评】本题考查了角平分线的性质、平行线的性质、含30°角的直角三角形的性质；熟练掌握角平分线的性质，证出∠EFG＝30°是解决问题的关键．
16．（3分）如图，△ABC中，AB＝AC，AD平分∠BAC，点E是线段BC延长线上一点，连接AE，点C在AE的垂直平分线上，若DE＝12cm，则△ABC的周长是 24cm ．
【分析】根据线段垂直平分线上的点到线段两端点的距离相等可得AC＝CE，根据等腰三角形三线合一的性质可得BD＝CD，然后求出AD+BD＝DE．
【解答】解：∵点C在AE的垂直平分线上，
∴AC＝CE，
∵AB＝AC，AD平分∠BAC，
∴BD＝CD，
∴AB+BD＝AC+CD＝CE+CD＝DE，
∵DE＝12cm，
∴AB+BC+AC＝AB+BD+AC+CD＝2×12＝24cm．
故答案为：24cm．
【点评】本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质，等腰三角形三线合一的性质，熟记性质并准确识图是解题的关键．
17．（3分）已知a＝8131，b＝2741，c＝961，则a、b、c的大小关系是 a＞b＞c ．
【分析】根据幂的乘方和积的乘方的运算法则求解．
【解答】解：a＝8131＝3124，
b＝2741＝3123，
c＝961＝3122，
∵a、b、c的底数相同，
∴a＞b＞c．
故答案为：a＞b＞c．
【点评】本题考查了幂的乘方，解答本题的关键是掌握幂的乘方和积的乘方的运算法则．
18．（3分）如图，已知四边形ABCD中，AB＝12厘米，BC＝8厘米，CD＝14厘米，∠B＝∠C，点E为线段AB的中点．如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时，点Q在线段CD上由C点向D点运动．当点Q的运动速度为 3或 厘米/秒时，能够使△BPE与以C、P、Q三点所构成的三角形全等．
【分析】分两种情况讨论，依据全等三角形的对应边相等，即可得到点Q的运动速度．
【解答】解：设点P运动的时间为t秒，则BP＝3t，CP＝8﹣3t，
∵∠B＝∠C，
∴①当BE＝CP＝6，BP＝CQ时，△BPE与△CQP全等，
此时，6＝8﹣3t，
解得t＝，
∴BP＝CQ＝2，
此时，点Q的运动速度为2÷＝3厘米/秒；
②当BE＝CQ＝6，BP＝CP时，△BPE与△CQP全等，
此时，3t＝8﹣3t，
解得t＝，
∴点Q的运动速度为6÷＝厘米/秒；
故答案为：3或．
【点评】本题考查了全等三角形的性质和判定的应用，解决问题的关键是掌握全等三角形的对应边相等．
三、解答题（共46分）
19．（6分）（1）计算：（a4）3+a8•a4；
（2）计算：[（x+y）m+n]2；
（3）已知2x+3y﹣2＝0，求9x•27y的值．
【分析】（1）应用幂的乘方与积的乘方及同底数幂乘法法则进行计算即可得出答案；
（2）应用幂的乘方法则进行计算即可得出答案；
（3）应用幂的乘法法则可得（32）x•（33）y，即可得出32x+3y，再由已知可得2x+3y＝2，代入计算即可得出答案．
【解答】解：（1）原式＝a4×3+a8+4
＝a12+a12
＝2a12；
（2）原式＝（x+y）2（m+n）；
（3）9x•27y＝（32）x•（33）y＝32x•33y＝32x+3y，
由2x+3y﹣2＝0，
可得2x+3y＝2，
原式＝32＝9．
【点评】本题主要考查了幂的乘方与积的乘方及同底数幂乘法，熟练掌握幂的乘方与积的乘方及同底数幂乘法法则进行求解是解决本题的关键．
20．（5分）点D为△ABC的边BC的延长线上的一点，DF⊥AB于点F，交AC于点E，∠A＝35°，∠D＝40°，求∠ACD的度数．
【分析】根据三角形外角的性质，得∠ACD＝∠B+∠A．欲求∠ACD，需求∠B．由DF⊥AB，得∠AFD＝90°．由∠AFD＝∠B+∠D，得∠B＝∠AFD﹣∠D＝50°．
【解答】解：∵DF⊥AB，
∴∠AFD＝90°．
∵∠AFD＝∠B+∠D，
∴∠B＝∠AFD﹣∠D＝90°﹣40°＝50°．
∴∠ACD＝∠B+∠A＝50°+35°＝85°．
【点评】本题主要考查三角形外角的性质、垂直，熟练掌握三角形外角的性质、垂直的定义是解决本题的关键．
21．（5分）已知：如图，C是线段AB的中点，CD＝CE，∠ACE＝∠BCD．求证：AD＝BE．
【分析】根据题意得出∠ACD＝∠BCE，AC＝BC，进而得出△ADC≌△BEC（SAS），根据全等三角形的性质即可得出答案．
【解答】证明：∵C是线段AB的中点，
∴AC＝BC，
∵∠ACE＝∠BCD，
∴∠ACD＝∠BCE，
在△ADC和△BEC中，
，
∴△ADC≌△BEC（SAS）．
∴AD＝BE．
【点评】此题考查了全等三角形的判定与性质，熟记全等三角形的判定与性质是解题的关键．
22．（6分）如图，点B、F、C、E在直线l上（F、C之间不能直接测量），点A、D在l异侧，测得AB＝DE，AB∥DE，∠A＝∠D．
（1）求证：△ABC≌△DEF；
（2）若BE＝10m，BF＝3m，求FC的长度．
【分析】（1）先证明∠ABC＝∠DEF，再根据ASA即可证明．
（2）根据全等三角形的性质即可解答．
【解答】（1）证明：∵AB∥DE，
∴∠ABC＝∠DEF，
在△ABC与△DEF中
∴△ABC≌△DEF（ASA）；
（2）∵△ABC≌△DEF，
∴BC＝EF，
∴BF+FC＝EC+FC，
∴BF＝EC，
∵BE＝10m，BF＝3m，
∴FC＝10﹣3﹣3＝4m．
【点评】本题考查全等三角形的判定和性质、平行线的判定等知识，解题的关键是正确寻找全等三角形的条件，记住平行线的判定方法，属于基础题，中考常考题型．
23．（5分）如图，已知A（﹣2，3），B（﹣3，1），C（1，﹣2）．
（1）请画出△ABC关于y轴对称的△A'B'C'；（其中A'、B'、C'分别是A，B，C的对应点，不写画法）
（2）A'、B'、C'的坐标分别为 （2，3），（3，1），（﹣1，﹣2）． ；
（3）△ABC的面积是 5.5 ．
【分析】（1）利用轴对称变换的性质分别作出A，B，C的对应点A′，B′，C′即可．
（2）根据A′，B′，C′的位置写出坐标即可．
（3）利用分割法把三角形面积看成矩形面积减去周围三个三角形面积即可．
【解答】解：（1）如图，△A'B'C'即为所求；
（2）A'、B'、C'的坐标分别为（2，3），（3，1），（﹣1，﹣2）．
故答案为：（2，3），（3，1），（﹣1，﹣2）．
（3）S△ABC＝4×5﹣×1×2﹣×3×4﹣×3×5＝5.5，
故答案为：5.5．
【点评】本题考查作图﹣复杂作图，三角形的面积等知识，解题的关键是掌握轴对称变换，学会用分割法求三角形面积．
24．（5分）如图，在△ABC中，∠C＝90°，AD平分∠CAB，DE⊥AB于点E，点F在AC上，BD＝DF．求证：BE＝FC．
【分析】根据角平分线的性质和全等三角形的判定方法可以证明△DCF和△DEB全等，从而可以证明结论成立．
【解答】证明：∵AD平分∠BAC，DE⊥AB，∠C＝90°，
∴DC＝DE，∠C＝∠DEA＝90°，
在Rt△DCF和Rt△DEB中，
，
∴Rt△DCF≌Rt△DEB（HL），
∴FC＝BE，
即BE＝FC．
【点评】本题考查全等三角形的判定与性质、角平分线的性质，解答本题的关键是明确题意，利用数形结合的思想解答．
25．（7分）已知：如图1，AB∥CD，请用尺规作图法，在射线CD上找一点P，使射线AP平分∠BAC．
小明的作图方法如下：
①以点A为圆心，适当长为半径画弧，交AB于点M，交AC于点N；
②分别以点M，N为圆心，大于MN的长为半径画弧，两弧在∠CAB的内部相交于点E；
③画射线AE，交射线CD于点P，点P即为所求．
小刚说：“我有不同的作法，如图2所示，只需要以点C为圆心，CA为半径画弧，交射线CD于点P，画射线AP，也能够得到AP平分∠BAC．
请回答：
（1）请补全小明的作图过程．小明在作图的过程中，构造出一组全等三角形，它们是 △AME ≌ △ANE ，全等的依据是 SSS ．因为全等三角形的对应角相等，所以能够得到∠CAB的角平分线AP；
（2）对于小刚的作图方法证明如下：
∵CA＝CP
∴∠CAP＝∠CPA（等边对等角）
∵AB∥CD
∴∠BAP＝∠ CPA （ 两直线平行，内错角相等 ）
∴∠CAP＝∠BAP
∴射线AP平分∠BAC．
（3）点P到直线AC和AB的距离相等，理由是 角平分线上的点到角的两边的距离相等 ．
【分析】（1）根据作法画出对应的几何图形，利用画法得到AM＝AN，ME＝NE，加上AE公共，则可根据“SSS”判断△AME≌△ANE，从而得到∠MAE＝∠NAE；
（2）利用等腰三角形的性质和平行线的性质证明∠CAP＝∠BAP；
（3）根据角平分线的性质求解．
【解答】解：（1）如图1，AP为所作，
在作图的过程中，构造出一组全等三角形，它们是△AME≌△ANE，全等的依据是SSS．因为全等三角形的对应角相等，所以能够得到∠CAB的角平分线AP；
（2）对于小刚的作图方法证明如下：
∵CA＝CP，
∴∠CAP＝∠CPA（等边对等角），
∵AB∥CD
∴∠BAP＝∠CPA（两直线平行，内错角相等），
∴∠CAP＝∠BAP，
∴射线AP平分∠BAC．
（3）点P到直线AC和AB的距离相等，理由是角平分线上的点到角的两边的距离相等．
故答案为△AME，△ANE，SSS；CPA，两直线平行，内错角相等；角平分线上的点到角的两边的距离相等．
【点评】本题考查了作图﹣复杂作图：解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了角平分线的性质和全等三角形的判定与性质．
26．（7分）课堂上，老师提出了这样一个问题：
如图1，在△ABC中，AD平分∠BAC交BC于点D，且AB+BD＝AC．
求证：∠ABC＝2∠ACB．
小明的方法是：如图2，在AC上截取AE，使AE＝AB，连接DE，构造全等三角形来证明结论．
（1）小天提出，如果把小明的方法叫做“截长法”，那么还可以用“补短法”通过延长线段AB构造全等三角形进行证明．辅助线的画法是：延长AB至F，使BF＝ BD ，连接DF．
请补全小天提出的辅助线的画法，并在图1中画出相应的辅助线；
（2）小芸通过探究，将老师所给的问题做了进一步的拓展，给同学们提出了如下的问题：
如图3，点D在△ABC的内部，AD，BD，CD分别平分∠BAC，∠ABC，∠ACB，且AB+BD＝AC．求证：∠ABC＝2∠ACB．
请你解答小芸提出的这个问题；
（3）小东将老师所给问题中的一个条件和结论进行交换，得到的命题如下：
如果在△ABC中，∠ABC＝2∠ACB，点D在边BC上，AB+BD＝AC，那么AD平分∠BAC．
小东判断这个命题也是真命题，老师说小东的判断是正确的．请你利用图4对这个命题进行证明．
【分析】（1）延长AB至F，使BF＝BD，连接DF，根据三角形的外角性质得到∠ABC＝2∠F，证明△ADF≌△ADC，根据全等三角形的性质证明结论；
（2）在AC上截取AE，使AE＝AB，连接DE，证明△ADB≌△ADE，根据全等三角形的性质证明结论；
（3）延长AB至G，使BG＝BD，连接DG，证明△ADG≌△ADC，根据全等三角形的性质、角平分线的定义证明．
【解答】证明：（1）延长AB至F，使BF＝BD，连接DF，
则∠BDF＝∠F，
∴∠ABC＝∠BDF+∠F＝2∠F，
∵AD平分∠BAC
∴∠BAD＝∠CAD，
∵AB+BD＝AC，BF＝BD，
∴AF＝AC，
在△ADF和△ADC中，
，
∴△ADF≌△ADC（SAS），
∴∠ACB＝∠F，
∴∠ABC＝2∠ACB；
（2）如图3，在AC上截取AE，使AE＝AB，连接DE，
∵AD，BD，CD分别平分∠BAC，∠ABC，∠ACB，
∴∠DAB＝∠DAE，∠DBA＝∠DBC，∠DCA＝∠DCB，
∵AB+BD＝AC，AE＝AB，
∴DB＝CE，
在△ADB和△ADE中，
，
∴△ADB≌△ADE（SAS），
∴BD＝DE，∠ABD＝∠AED，
∴DE＝CE，
∴∠EDC＝∠ECD，
∴∠AED＝2∠ECD，
∴∠ABD＝2∠ECD，
∴∠ABC＝2∠ACB；
（3）如图4，延长AB至G，使BG＝BD，连接DG，
则∠BDG＝∠AGD，
∴∠ABC＝∠BDG+∠G＝2∠AGD，
∵∠ABC＝2∠ACB，
∴∠AGD＝∠ACB，
∵AB+BD＝AC，BG＝BD，
∴AG＝AC，
∴∠AGC＝∠ACG，
∴∠DGC＝∠DCG，
∴DG＝DC，
在△ADG和△ADC中，
，
∴△ADG≌△ADC（SSS），
∴∠DAG＝∠DAC，即AD平分∠BAC．
【点评】本题考查的是三角形全等的判定和性质、角平分线的定义，掌握全等三角形的判定定理和性质定理是解题的关键．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2023/7/10 12:19:49；用户：笑涵数学；邮箱：15699920825；学号：36906111