新高考数学一轮复习讲练测专题5.5函数y＝Asin(ωx＋φ)的图象及其应用（讲）（2份打包，原卷版+解析版）

这是一份新高考数学一轮复习讲练测专题5.5函数y＝Asin(ωx＋φ)的图象及其应用（讲）（2份打包，原卷版+解析版），文件包含新高考数学一轮复习讲练测专题55函数y＝Asinωx＋φ的图象及其应用讲原卷版doc、新高考数学一轮复习讲练测专题55函数y＝Asinωx＋φ的图象及其应用讲解析版doc等2份试卷配套教学资源，其中试卷共29页， 欢迎下载使用。

知识点1．求三角函数解析式
（1）的有关概念
（2）用五点法画一个周期内的简图
用五点法画一个周期内的简图时，要找五个关键点，如下表所示：
知识点2．三角函数图象的变换
1.函数图象的变换（平移变换和上下变换）
平移变换：左加右减，上加下减
把函数向左平移个单位，得到函数的图象;
把函数向右平移个单位，得到函数的图象;+网】
把函数向上平移个单位，得到函数的图象;
把函数向下平移个单位，得到函数的图象.
伸缩变换:
把函数图象的纵坐标不变,横坐标伸长到原来的，得到函数的图象;
把函数图象的纵坐标不变,横坐标缩短到原来的，得到函数的图象;
把函数图象的横坐标不变,纵坐标伸长到原来的，得到函数的图象;
把函数图象的横坐标不变,纵坐标缩短到原来的，得到函数的图象.
2. 由的图象变换出的图象一般有两个途径，只有区别开这两个途径，才能灵活进行图象变换,利用图象的变换作图象时，提倡先平移后伸缩，但先伸缩后平移也经常出现无论哪种变形，请切记每一个变换总是对字母而言，即图象变换要看“变量”起多大变化，而不是“角变化”多少.
途径一：先平移变换再周期变换(伸缩变换)先将的图象向左或向右平移个单位，再将图象上各点的横坐标变为原来的倍()，便得的图象.
途径二：先周期变换(伸缩变换)再平移变换：先将的图象上各点的横坐标变为原来的倍()，再沿轴向左()或向右()平移个单位，便得的图象.
注意：函数的图象，可以看作把曲线上所有点向左(当时)或向右(当时)平行移动个单位长度而得到.
知识点3．函数的图象与性质的综合应用
（1）的递增区间是，递减区间是.
（2）对于和来说，对称中心与零点相联系，对称轴与最值点联系.
的图象有无穷多条对称轴，可由方程解出；它还有无穷多个对称中心，它们是图象与轴的交点，可由，解得，即其对称中心为．
（3）若为偶函数，则有;若为奇函数则有.
（4）的最小正周期都是.
【考点分类剖析】
考点一 求三角函数解析式
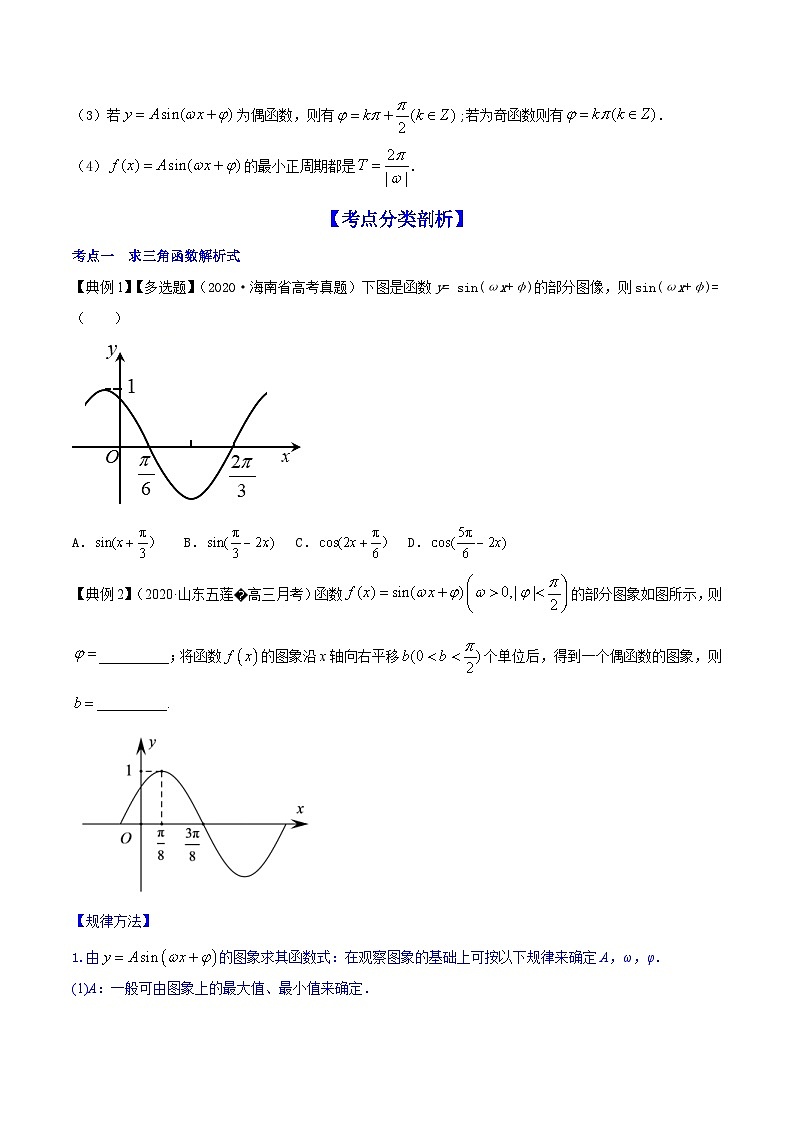
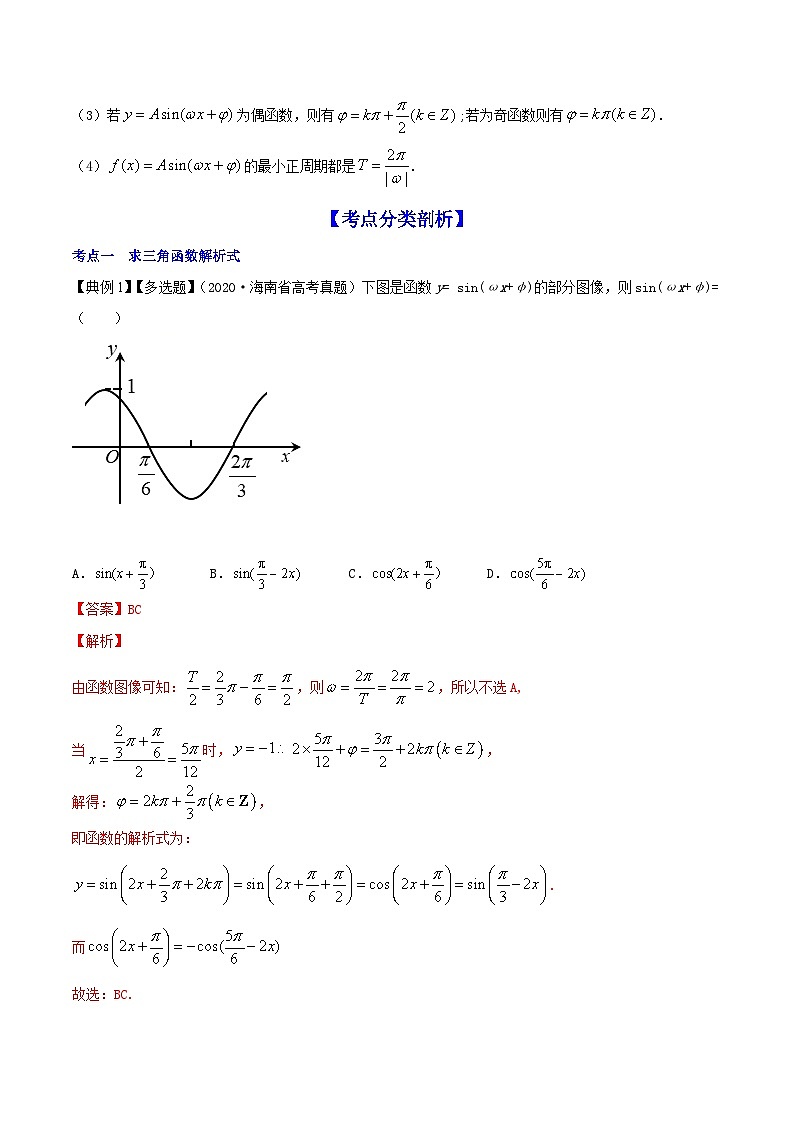
【典例1】【多选题】（2020·海南省高考真题）下图是函数y= sin(ωx+φ)的部分图像，则sin(ωx+φ)= （ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【典例2】（2020·山东五莲�高三月考）函数的部分图象如图所示，则__________；将函数的图象沿x轴向右平移个单位后，得到一个偶函数的图象，则__________.
【规律方法】
1.由的图象求其函数式：在观察图象的基础上可按以下规律来确定A，ω，φ．
(1)A：一般可由图象上的最大值、最小值来确定．
(2)ω：因为T＝eq \f(2π,ω)，故往往通过求周期T来确定ω.可通过已知曲线与x轴的交点来确定T，即相邻的最高点与最低点之间的距离为eq \f(T,2)；相邻的两个最高点(或最低点)之间的距离为T．
(3)φ：从“五点法”中的第一个点(－eq \f(φ,ω)，0)(也叫初始点)作为突破口，要从图象的升降情况找准第一个点的位置．
依据五点列表法原理，点的序号与式子的关系如下：
“第一点”(即图象上升时与x轴的交点)为ωx＋φ＝0；
“第二点”(即图象曲线的“峰点”)为ωx＋φ＝eq \f(π,2)；
“第三点”(即图象下降时与x轴的交点)为ωx＋φ＝π；
“第四点”(即图象曲线的“谷点”)为ωx＋φ＝eq \f(3π,2)；
“第五点”(即图象第二次上升时与x轴的交点)为ωx＋φ＝2π．
在用以上方法确定φ的值时，还要注意题目中给出的φ的范围，不在要求范围内的要通过周期性转化到要求范围内．
(4)A，ω，φ三个量中初相φ的确定是一个难点，除使用初始点(－eq \f(φ,ω)，0)外，还可在五点中找两个特殊点列方程组来求解φ．
2.利用图象变换求解析式：
由的图象向左或向右平移个单位，得到函数，将图象上各点的横坐标变为原来的倍()，便得，将图象上各点的纵坐标变为原来的倍()，便得.
【变式探究】
1. （2020·湖南娄星�娄底一中高一期末）将函数的图象向左平移个单位长度后得到曲线，再将上所有点的横坐标伸长到原来的2倍得到曲线，则的解析式为（ ）
A．B．
C．D．
2.（2020·江苏南通�高三其他）已知函数的最小正周期是，若将该函数的图象向右平移个单位长度后得到的图象关于原点对称，则函数的解析式________.
【总结提升】
根据函数的图象确定函数中的参数的主要方法：
（1）主要是根据图象的最高点或最低点的纵坐标确定；
（2）主要由最小正周期确定，而的值主要是根据一个周期内图象的零点与最值点的横坐标确定；
（3）主要是由图象的特殊点的坐标确定．
考点二 三角函数图象的变换
【典例3】（2021·黑龙江佳木斯市·佳木斯一中高三三模（理））将函数f(x)的图象向左平移 SKIPIF 1 < 0 个单位长度，再将所得函数图象上的所有点的横坐标变为原来的 SKIPIF 1 < 0 倍，得到函数g(x)＝Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的图象．已知函数g(x)的部分图象如图所示，则下列关于函数f(x)的说法正确的是（ ）

A．f(x)的最小正周期为 SKIPIF 1 < 0
B．f(x)在区间 SKIPIF 1 < 0 上单调递减
C．f(x)的图象关于直线x＝ SKIPIF 1 < 0 对称
D．f(x)的图象关于点 SKIPIF 1 < 0 成中心对称
【典例4】【多选题】（2021·辽宁实验中学高三其他模拟）为得到函数 SKIPIF 1 < 0 的图象，只需将 SKIPIF 1 < 0 的图象（ ）
A．先将横坐标扩大到原来的2倍(纵坐标不变)，再向右平移 SKIPIF 1 < 0 个单位长度
B．先将横坐标扩大到原来的2倍(纵坐标不变)，再向右平移 SKIPIF 1 < 0 个单位长度
C．先向右平移 SKIPIF 1 < 0 个单位长度，再将横坐标扩大到原来的2倍(纵坐标不变)
D．先向右平移 SKIPIF 1 < 0 个单位长度，再将横坐标扩大到原来的2倍(纵坐标不变)
【规律方法】
函数的图象变换除了平移变换外，还有对称变换．如本例．一般地，函数f(x)的图象与f(－x)的图象关于y轴对称；－f(x)的图象与f(x)的图象关于x轴对称；－f(－x)的图象与f(x)的图象关于原点对称；f(|x|)的图象关于y轴对称．
【变式探究】
1.（2020·浙江高一单元测试）如图是函数在区间上的图象．为了得到这个函数的图象，只要将的图象上所有的点（ ）．
A．向左平移个单位长度，再把所得各点的横坐标缩短到原来的，纵坐标不变
B．向左平移个单位长度，再把所得各点的横坐标仲长到原来的，纵坐标不变
C．把所得各点的横坐标缩短到原来的，纵坐标不变，再向左平移个单位长度
D．向左平移个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变
2.【多选题】（2021·江苏高三其他模拟）将函数 SKIPIF 1 < 0 图象上各点的横坐标伸长到原来的2倍(纵坐标不变)，再向右平移 SKIPIF 1 < 0 个单位长度后，得到函数 SKIPIF 1 < 0 的图象，则下列结论中正确的有（ ）
A．函数 SKIPIF 1 < 0 的最大值为2B．函数 SKIPIF 1 < 0 的图象关于点 SKIPIF 1 < 0 对称
C．函数 SKIPIF 1 < 0 是偶函数D．直线 SKIPIF 1 < 0 是函数 SKIPIF 1 < 0 图象的一条对称轴
【特别提醒】
1.图象的左右平移是针对x而言的，即平移多少是指自变量“x”的变化，x系数为1，而不是对“ωx＋φ”而言的．
2．图象的伸缩变换即周期变换也是针对x而言的，即只是自变量x的系数发生改变，变为原来的eq \f(1,ω)倍，而不涉及φ．
3.在进行图象变换时，先平移后伸缩与先伸缩后平移是两种不同的变换，且这两种变换中，平移的单位长度不同，前者平移了|φ|个单位长度，而后者平移了|eq \f(φ,ω)|个单位长度，这是因为由y＝sinωx的图象变换为y＝sin(ωx＋φ)的图象的过程中，各点的横坐标增加或减少了|eq \f(φ,ω)|个单位长度，即x→x＋eq \f(φ,ω)，ωx→ωx＋φ．
考点三 三角函数模型的应用
【典例5】【多选题】（2021·广东深圳市·高三二模）摩天轮常被当作一个城市的地标性建筑，如深圳前海的“湾区之光”摩天轮，如图所示，某摩天轮最高点离地面高度128米，转盘直径为120米，设置若干个座舱，游客从离地面最近的位置进舱，开启后按逆时针匀速旋转 SKIPIF 1 < 0 分钟，当 SKIPIF 1 < 0 时，游客随舱旋转至距离地面最远处．以下关于摩天轮的说法中，正确的为（ ）
A．摩天轮离地面最近的距离为4米
B．若旋转 SKIPIF 1 < 0 分钟后，游客距离地面的高度为 SKIPIF 1 < 0 米，则 SKIPIF 1 < 0
C．若在 SKIPIF 1 < 0 ， SKIPIF 1 < 0 时刻，游客距离地面的高度相等，则 SKIPIF 1 < 0 的最小值为30
D． SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，使得游客在该时刻距离地面的高度均为90米
【典例6】平潭国际“花式风筝冲浪”集训队，在平潭龙凤头海滨浴场进行集训，海滨区域的某个观测点观测到该处水深（米）是随着一天的时间呈周期性变化，某天各时刻的水深数据的近似值如下表：
（Ⅰ）根据表中近似数据画出散点图（坐标系在答题卷中）.观察散点图，从
①， ②，③
中选择一个合适的函数模型，并求出该拟合模型的函数解析式；（Ⅱ）为保证队员安全，规定在一天中的5～18时且水深不低于1.05米的时候进行训练，根据（Ⅰ） 中的选择的函数解析式，试问：这一天可以安排什么时间段组织训练，才能确保集训队员的安全.
【规律方法】
三角函数模型的应用体现在两方面：一是已知函数模型求解数学问题；二是把实际问题抽象转化成数学问题，建立数学模型再利用三角函数的有关知识解决问题．
【变式探究】
（2021·全国高一课时练习）如图是一半径为2米的水轮，水轮的圆心 SKIPIF 1 < 0 距离水面1米，已知水轮自点 SKIPIF 1 < 0 开始以1分钟旋转4圈的速度顺时针旋转，点 SKIPIF 1 < 0 距水面的高度 SKIPIF 1 < 0 （米 SKIPIF 1 < 0 与时间 SKIPIF 1 < 0 （秒 SKIPIF 1 < 0 满足函数关系式 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 __， SKIPIF 1 < 0 __．
考点四 函数的图象与性质的综合应用
【典例7】(2019年高考全国Ⅲ卷文)函数在[0，2π]的零点个数为（ ）
A．2 B．3
C．4D．5
【典例8】(2019年高考浙江卷)设函数.
（1）已知函数是偶函数，求的值；
（2）求函数的值域．
【典例9】（2017·山东高考真题（理））设函数，其中.已知.
（Ⅰ）求；
（Ⅱ）将函数的图象上各点的横坐标伸长为原来的2倍（纵坐标不变），再将得到的图象向左平移个单位，得到函数的图象，求在上的最小值.
【规律方法】
1.方程根的个数可转化为两个函数图象的交点个数．
2.研究y＝Asin(ωx＋φ)的性质时可将ωx＋φ视为一个整体，利用换元法和数形结合思想进行解题．
【变式探究】
1. （2021·江西新余市·高一期末（理））已知函数 SKIPIF 1 < 0 .
（1）已知 SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的值；
（2）当 SKIPIF 1 < 0 时，不等式 SKIPIF 1 < 0 恒成立，求实数 SKIPIF 1 < 0 的取值范围.
2. （2020·全国高三（文））已知，函数．
（Ⅰ）若，求的单调递增区间；
（Ⅱ）若的最大值是，求的值．
新课程考试要求
了解函数 y＝A sin (ωx＋φ) 的物理意义，掌握 y＝A sin (ωx＋φ) 的图象，了解参数 A，ω，φ 对函数图象变化的影响.
核心素养
本节涉及所有的数学核心素养：逻辑推理（多例）、直观想象（多例）、数学运算（多例）、数据分析（例6）等.
高考预测
（1） “五点法”作图；
（2）函数图象的变换；
（3）三角函数模型的应用问题.
（4）对于三角恒等变换，高考命题主要以公式的基本运用（正用、逆用、变用）、计算为主，其中多与角的范围、三角函数的性质、三角形等知识结合考查.
，
表示一个振动量时
振幅
周期
频率
相位
初相
－
0
3
6
9
12
15
18
21
24
1.5
2．4
1.5
0．6
1.4
2.4
1.6
0.6
1.5