





中职数学高教版(2021·十四五)拓展模块一(上册)第3章 圆锥曲线3.3 抛物线评优课ppt课件
展开平南三桥位于广西壮族自治区,是2020 年建成的世界上最大的跨径拱桥,多项技术填补了世界拱桥空白,成为“中国桥梁”建造的新名片. 观察下图,桥拱的轮廓线是什么图形?有什么特点?
可以看出,拱桥的轮廓线是一条形如彩虹的曲线,人们称之为抛物线。那么,如何画出抛物线呢?
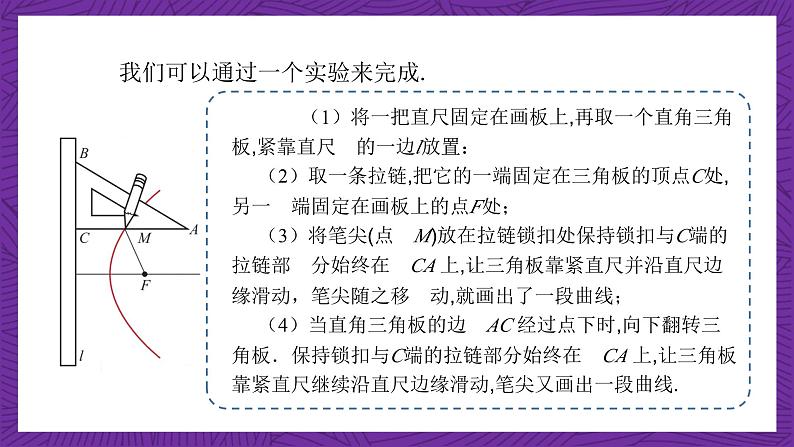
我们可以通过一个实验来完成.
(1)将一把直尺固定在画板上,再取一个直角三角板,紧靠直尺 的一边l放置: (2)取一条拉链,把它的一端固定在三角板的顶点C处,另一 端固定在画板上的点F处; (3)将笔尖(点 M)放在拉链锁扣处保持锁扣与C端的拉链部 分始终在 CA 上,让三角板靠紧直尺并沿直尺边缘滑动,笔尖随之移 动,就画出了一段曲线; (4)当直角三角板的边 AC 经过点下时,向下翻转三角板.保持锁扣与C端的拉链部分始终在 CA 上,让三角板靠紧直尺继续沿直尺边缘滑动,笔尖又画出一段曲线.
一般地,把平面内与一个定点F和一条定直线 l 的距离相等的点的轨迹称为抛物线.定点 F 称为抛物线的焦点,定直线 l 称为抛物线的准线.
显然,笔尖(即点M )始终保持到定点 F 的距离与到直尺边 l 的距离相等(|MF|=|MC|).
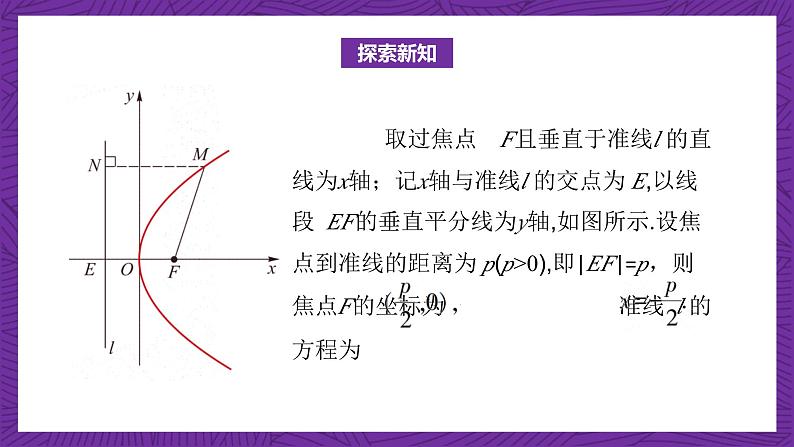
我们从椭圆和双曲线的定义出发,通过建立合适的平面直角坐标系,分别求出了椭圆和双曲线的方程.那么,如何从抛物线的定义出发,建立恰当的平面直角坐标系来求出抛物线的方程呢?
设M(x,y)为抛物线上的任意一点,点M到l的距离为|MN|,则有 |MF|=|MN|.于是,可得 将上式两边平方得展开并整理得 y²=2px(p>0).
上面方程称为抛物线的标准方程.
类似地,通过建立不同的平面直角坐标系,可以得到抛物线其他三种形式的标准方程:y²=-2px, x² =2py, x² =-2py. 它们的焦点坐标、准线方程及图形归纳见表:
判断抛物线的焦点在哪个坐标轴上是解决有关抛物线问题的关键,为此可将抛物线方程化为标准方程,观察标准方程中的一次项,如果一次项含变量x,并且系数为正(或为负),则焦点在x轴的正半轴(或负半轴)上;如果一次项含变量,并且系数为正(或为负),则焦点在y轴的正半轴(或负半轴)上.
为什么拱桥的桥拱大多设计为抛物线的形状?
当问题中没有明确指出抛物线的焦点位置或对称轴时,一般需要分情况讨论.
1. 根据条件,求抛物线的标准方程. (1)准线方程为 x=4; (2)焦点为F(0,-3); (3)关于x轴对称,且过点(5,-4); (4)对称轴为坐标轴,且过点(6,3).
2. 在直角坐标系中,画出下列拋物线的图像. (1) y²=-6x ; (2)x²=9y. 3. 已知拋物线的顶点为坐标原点,焦点在x轴上,抛物线上一点P(-3,m)到焦点的距离为5,求拋物线的标准方程. 4.已知垂直于x轴的直线交抛物线 y²=6x于A、B两点,且 求直线AB的方程,
1.书面作业:完成课后习题和《学习指导与练习》;2.查漏补缺:根据个人情况对课堂学习复习与回顾;3.拓展作业:阅读教材扩展延伸内容.
高教版(2021·十四五)拓展模块一(上册)4.1 平面完美版ppt课件: 这是一份高教版(2021·十四五)拓展模块一(上册)<a href="/sx/tb_c4053644_t3/?tag_id=26" target="_blank">4.1 平面完美版ppt课件</a>,共42页。PPT课件主要包含了情境导入,平面的特征和表示,探索新知,典型例题,巩固练习,平面的基本性质,归纳总结,布置作业等内容,欢迎下载使用。
数学拓展模块一(上册)3.1 椭圆评优课课件ppt: 这是一份数学拓展模块一(上册)<a href="/sx/tb_c4053630_t3/?tag_id=26" target="_blank">3.1 椭圆评优课课件ppt</a>,共44页。PPT课件主要包含了情境导入,探索新知,椭圆的标准方程,典型例题,巩固练习,椭圆的几何性质,归纳总结,布置作业等内容,欢迎下载使用。
数学拓展模块一(上册)3.3.2 抛物线的几何性质试讲课ppt课件: 这是一份数学拓展模块一(上册)<a href="/sx/tb_c4053640_t3/?tag_id=26" target="_blank">3.3.2 抛物线的几何性质试讲课ppt课件</a>,共16页。PPT课件主要包含了探索新知,典型例题,巩固练习,归纳总结,布置作业,情境导入,对称性,离心率等内容,欢迎下载使用。












