新高考数学一轮复习(举一反三)重难点题型精练专题3.5 导数与函数的极值、最值（2份打包，原卷版+解析版）

这是一份新高考数学一轮复习(举一反三)重难点题型精练专题3.5 导数与函数的极值、最值（2份打包，原卷版+解析版），文件包含新高考数学一轮复习举一反三重难点题型精练专题35导数与函数的极值最值原卷版doc、新高考数学一轮复习举一反三重难点题型精练专题35导数与函数的极值最值解析版doc等2份试卷配套教学资源，其中试卷共28页， 欢迎下载使用。

1．函数的极值与导数
2．函数的最值
(1)在闭区间[a，b]上连续的函数f (x)在[a，b]上必有最大值与最小值．
(2)若函数f (x)在[a，b]上单调递增，则f (a)为函数的最小值，f (b)为函数的最大值；若函数f (x)在[a，b]上单调递减，则f (a)为函数的最大值，f (b)为函数的最小值．
【题型1 根据函数图象判断极值】
【方法点拨】
由图象判断函数y＝f(x)的极值，要抓住两点：
(1)由y＝f′(x)的图象与x轴的交点，可得函数 y＝f(x)的可能极值点；
(2)由导函数y＝f′(x)的图象可以看出y＝f′(x)的值的正负，从而可得函数y＝f(x)的单调性．两者结合可得极
值点.
【例1】（2022春•杨浦区校级期末）已知函数y＝f（x）（a＜x＜b）的导函数是y＝f'（x）（a＜x＜b），导函数y＝f'（x）的图象如图所示，则函数y＝f（x）在（a，b）内有（ ）
A．3个驻点B．4个极值点
C．1个极小值点D．1个极大值点
【解题思路】由题意结合导函数图像即可确定函数的性质．
【解答过程】解：由导函数的图象可知，原函数存在4个驻点，函数有3个极值点，其中2个极大值点，1个极小值点．
故选：C．
【变式1-1】（2022春•纳雍县期末）已知函数f（x）的导函数的图像如图所示，则下列结论正确的是（ ）
A．﹣1是f（x）的极小值点
B．曲线y＝f（x）在x＝2处的切线斜率小于零
C．f（x）在区间（﹣∞，3）上单调递减
D．﹣3是f（x）的极小值点
【解题思路】根据题意，由函数导数与单调性的关系依次分析选项，即可得答案．
【解答过程】解：根据题意，依次分析选项：
对于A，在x＝﹣1左右都有f′（x）＜0，﹣1不是f（x）的极值，A错误；
对于B，f′（x）的图象在（﹣3，3）上，f′（x）＜0，f（x）为减函数，则曲线y＝f（x）在x＝2处的切线斜率即f′（2）小于零，B正确；
对于C，f′（x）的图象在（﹣∞，﹣3）上，f′（x）＞0，f（x）为增函数，C错误；
对于D，f′（x）的图象在（﹣∞，﹣3）上，f′（x）＞0，在（﹣3，3）上，f′（x）＜0，则﹣3是f（x）的极大值点，D错误；
故选：B．
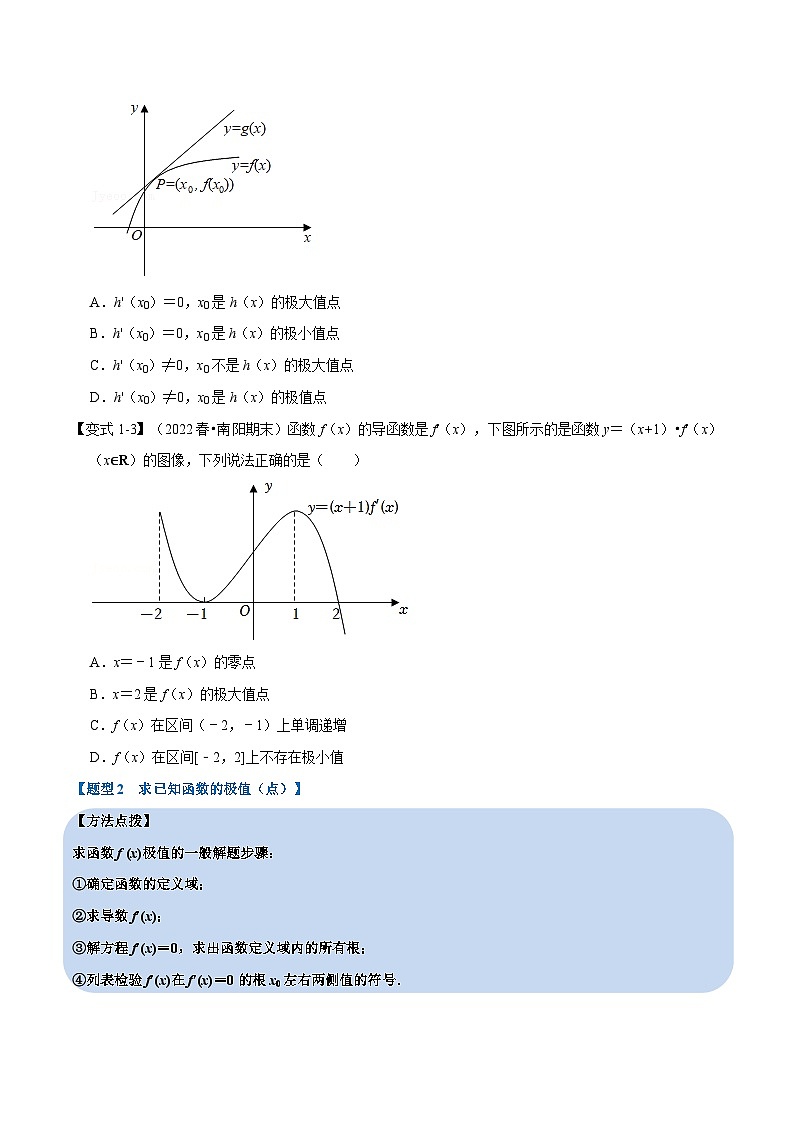
【变式1-2】（2022春•朝阳区校级月考）如图，可导函数y＝f（x）在点P（x0，f（x0））处的切线方程为y＝g（x），设h（x）＝g（x）﹣f（x），h'（x）为h（x）的导函数，则下列结论中正确的是（ ）
A．h'（x0）＝0，x0是h（x）的极大值点
B．h'（x0）＝0，x0是h（x）的极小值点
C．h'（x0）≠0，x0不是h（x）的极大值点
D．h'（x0）≠0，x0是h（x）的极值点
【解题思路】由图判断函数h（x）的单调性，结合y＝g（x）为y＝f（x）在点P处的切线方程，则有h'（x0）＝0，由此可判断极值情况．
【解答过程】解：由题得，当x∈（﹣∞，x0）时，h（x）单调递减，
当x∈（x0，+∞）时，h（x）单调递增，
又h'（x0）＝g'（x0）﹣f'（x0）＝0，
则有x0是h（x）的极小值点，
故选：B．
【变式1-3】（2022春•南阳期末）函数f（x）的导函数是f'（x），下图所示的是函数y＝（x+1）•f'（x）（x∈R）的图像，下列说法正确的是（ ）
A．x＝﹣1是f（x）的零点
B．x＝2是f（x）的极大值点
C．f（x）在区间（﹣2，﹣1）上单调递增
D．f（x）在区间[﹣2，2]上不存在极小值
【解题思路】根据函数y＝（x+1）•f'（x）（x∈R）的图像判断f′（x）的符号，进而判断f（x）的单调性和极值即可．
【解答过程】解：由函数y＝（x+1）•f'（x）（x∈R）的图像知，
当﹣2＜x＜﹣1时，x+1＜0，y＞0，∴f'（x）＜0，f（x）在（﹣2，﹣1）上减函数，
当﹣1＜x＜2时，x+1＞0，y＞0，∴f'（x）＞0，f（x）在（﹣1，2）上增函数，
当x＞2时，x+1＞0，y＜0，f'（x）＜0，f（x）在（2，+∞）上减函数，
∴x＝﹣1、x＝2分别是f（x）的极小值点、极大值点．
∴选项A、C、D错误，选项B正确，
故选：B．
【题型2 求已知函数的极值（点）】
【方法点拨】
求函数f (x)极值的一般解题步骤：
①确定函数的定义域；
②求导数f′(x)；
③解方程f′(x)＝0，求出函数定义域内的所有根；
④列表检验f′(x)在f′(x)＝0的根x0左右两侧值的符号．
【例2】（2022•扬中市校级开学）已知函数在上的极小值为（ ）
A．B．C．D．
【解题思路】根据极小值的定义，结合导数的性质进行求解即可．
【解答过程】解：由，
当时，f′（x）＜0，f（x）单调递减，
当时，f′（x）＞0，f（x）单调递增，所以是函数的极小值点，
极小值为：，
故选：D．
【变式2-1】（2022春•资阳期末）函数f（x）＝x3﹣3x的极大值为（ ）
A．﹣4B．﹣2C．1D．2
【解题思路】求导，利用导数确定f（x）的单调区间，从而即可求极大值．
【解答过程】解：因为f（x）＝x3﹣3x，x∈R，
所以f′（x）＝3x2﹣3＝3（x+1）（x﹣1），
令f′（x）＝0，得x＝﹣1或x＝1，
所以当x＜﹣1时，f′（x）＞0，f（x）单调递增；当﹣1＜x＜1时，f′（x）＜0，f（x）单调递减；当x＞1时，f′（x）＞0，f（x）单调递增；
所以f（x）的单调递增区间为：（﹣∞，﹣1），（1，∞）；单调递减区间为（﹣1，1）．
所以f（x）极大值＝f（﹣1）＝2．
故选：D．
【变式2-2】（2022春•平谷区期末）函数f（x）＝x+2csx在[0，π]上的极小值点为（ ）
A．B．C．D．
【解题思路】分析函数导数的符号变化，由此可得函数的单调性，由单调性得出结论即可．
【解答过程】解：对于函数f（x）＝x+2csx，f′（x）＝1﹣2sinx，
因为x∈[0，π]，当时，f′（x）＞0，
当时，f′（x）＜0，当时，f′（x）＞0，
所以f（x）在区间上是增函数，在区间上是减函数，在是增函数．
因此，函数f（x）＝x+2csx在[0，π]上的极小值点为．
故选：C．
【变式2-3】（2022春•新乡期末）已知函数f（x）＝（x﹣1）2（2﹣x）3，则f（x）的极大值点为（ ）
A．1B．C．﹣1D．2
【解题思路】解：因为f'（x）＝2（x﹣1）（2﹣x）3﹣3（x﹣1）2（2﹣x）2＝（x﹣1）（2﹣x）2（7﹣5x），
所以f（x）在（﹣∞，1），上单调递减，在上单调递增，
所以f（x）的极大值点为，
故选：B．
【解答过程】解：f'（x）＝2（x﹣1）（2﹣x）3﹣3（x﹣1）2（2﹣x）2＝（x﹣1）（2﹣x）2（7﹣5x），
令f′（x）＝0得x＝1或x，
所以f（x）在（﹣∞，1），上单调递减，在上单调递增，
所以f（x）的极大值点为，
故选：B．
【题型3 由函数的极值（点）求参数】
【方法点拨】
根据函数极值情况求参数的两个要领：
①列式：根据极值点处导数为0和极值这两个条件列方程组，利用待定系数法求解．
②验证：求出参数后，验证所求结果是否满足题意．
【例3】（2022春•龙海市校级期末）函数f（x）＝4x3﹣ax2﹣2bx+2在x＝1处有极大值﹣3，则a﹣b的值等于（ ）
A．0B．6C．3D．2
【解题思路】对函数求导，利用f（1）＝﹣3以及f′（1）＝0解出a，b，进而得出答案．
【解答过程】解：由题意得f′（x）＝12x2﹣2ax﹣2b，因为f（x）在x＝1处有极大值﹣3，
所以f′（1）＝12﹣2a﹣2b＝0，f（1）＝4﹣a﹣2b+2＝﹣3，解得a＝3，b＝3，
所以a﹣b＝0．
故选：A．
【变式3-1】（2022春•哈尔滨期末）若函数有2个极值点，则实数a的取值范围是（ ）
A．（﹣∞，6）∪（6，+∞）B．（0，6）∪（6，+∞）
C．{6}D．（0，+∞）
【解题思路】根据条件函数f（x）有两个极值点，转化为方程f′（x）＝0有两个不等正实数根，得到求解．
【解答过程】解：函数f（x）的定义域（0，+∞），，
令f′（x）＝0得，x＝6或x＝a，
∵函数f（x）有2个极值点，∴f'（x）＝0有2个不同的正实数根，∴a＞0且a≠6，
故选：B．
【变式3-2】（2022春•淄博期末）已知x＝2是函数f（x）＝ax3﹣3x2+a的极小值点，则f（x）的极大值为（ ）
A．﹣3B．0C．1D．2
【解题思路】先对函数求导，然后结合极值存在条件可求a，进而可求函数的极大值．
【解答过程】解：因为f′（x）＝3ax2﹣6x，
由题意可得，f′（2）＝12a﹣12＝0，
故a＝1，f′（x）＝3x2﹣6x，
当x＞2或x＜0时，f′（x）＞0，函数单调递增，当0＜x＜2时，f′（x）＜0，函数单调递减，
故当x＝0时，函数取得极大值f（0）＝1．
故选：C．
【变式3-3】（2022春•赣州期末）已知函数f（x）＝x3+a2x2+（2b2﹣7）x+1（a＞0，b＞0）在x＝1处取得极值，则a+b的最大值为（ ）
A．1B．C．2D．
【解题思路】根据题意，对函数求导，令f′（1）＝0可求得a2+b2＝2，利用基本不等式可求a+b的最大值．
【解答过程】解：函数f（x）＝x3+a2x2+（2b2﹣7）x+1（a＞0，b＞0）的导数为f′（x）＝3x2+2a2x+2b2﹣7，
因为函数在x＝1处取得极值，
所以f′（1）＝3+2a2+2b2﹣7＝0，
即a2+b2＝2，
因为a2+b2＝（a+b）2﹣2ab＝2，即（a+b）2﹣2＝2ab，
因为，所以，
整理得（a+b）2≤4，所以a+b≤2，当且仅当a＝b＝1时等号成立，
此时f′（x）＝3x2+2x﹣5＝（3x+5）（x﹣1），满足函数在x＝1处取得极值，
所以a+b的最大值为2，
故选：C．
【题型4 利用导数求函数的最值】
【方法点拨】
(1)若函数f (x)在闭区间[a，b]上单调递增或单调递减，f (a)与f (b)一个为最大值，一个为最小值．
(2)若函数f (x)在闭区间[a，b]内有极值，要先求出[a，b]上的极值，与f (a)，f (b)比较，最大的是最大值，
最小的是最小值，可列表完成．
(3)函数f (x)在区间(a，b)上有唯一一个极大(或极小)值点，这个极值点就是最大(或最小)值点，此结论在导
数的实际应用中经常用到．
【例4】（2022•河南开学）函数在（0，+∞）上的最小值为（ ）
A．2B．3C．4D．5
【解题思路】由题意求导，从而确定函数的单调性，从而求函数的最值．
【解答过程】解：因为，
所以f（x）在（0，2）上单调递减，在（2，+∞）上单调递增，
故f（x）min＝f（2）＝4．
故选：C．
【变式4-1】（2022春•中山市校级月考）函数y＝x﹣2sinx在区间[0，2]上的最小值是（ ）
A．B．C．D．
【解题思路】利用导数研究函数区间单调性，进而求其最小值即可．
【解答过程】解：由y′＝1﹣2csx，
当时，y′＜0，即y递减；
当时，y′＞0，即y递增；
所以．
故选：D．
【变式4-2】（2022春•乐山期末）已知函数f（x）＝x2﹣lnx，则函数f（x）在[1，2]上的最小值为（ ）
A．1B．C．D．
【解题思路】求导确定函数在[1，2]上的单调性，求出最小值即可．
【解答过程】解：因为f（x）＝x2﹣lnx（x＞0），所以f′（x）＝2x，
所以当x∈[1，2]时，f′（x）0，则f（x）在[1，2]上单调递增，则f（x）在[1，2]上的最小值为f（1）＝1．
故选：A．
【变式4-3】（2022•绿园区校级开学）函数f（x）＝lnx与g（x）＝xex﹣lnx﹣x的最小值分别为a，b，则（ ）
A．a＝bB．a＞b
C．a＜bD．a，b的大小不能确定
【解题思路】根据函数的单调性分别求出函数f（x），g（x）的最小值，比较a，b即可．
【解答过程】解：f（x）的定义域是（0，+∞），
，
令f′（x）＜0，解得：0＜x＜1，令f′（x）＞0，解得：x＞1，
f（x）在（0，1）递减，在（1，+∞）递增，
f（x）的最小值是f（1）＝1，故a＝1，
g（x）＝xex﹣lnx﹣x，定义域（0，+∞），
，
令h（x）＝xex﹣1，则h′（x）＝（x+1）ex＞0，x∈（0，+∞），
则可得h（x）在（0，+∞）上单调递增，且h（0）＝﹣1＜0，h（1）＝e﹣1＞0，
故存在x0∈（0，1）使得h（x）＝0即，即x0+lnx0＝0，
当x∈（0，x0）时，h（x）＜0，g′（x）＜0，函数g（x）单调递减，
当x∈（x0，+∞）时，g′（x）＞0，函数g（x）单调递增，
故当x＝x0时，函数取得最小值，即b＝1，
所以a＝b，
故选：A．
【题型5 由函数的最值求参数】
【例5】（2022春•烟台期末）若函数在区间[1，2]上的最小值为0，则实数a的值为（ ）
A．﹣2B．﹣1C．2D．
【解题思路】对函数求导后，分a≤0和a＞0两种情况求出函数的单调区间，从而可求出函数的最小值，使最小值等于零，从而可出实数a的值．
【解答过程】解：由，得f'（x）＝3x2﹣3ax＝3x（x﹣a），
当a≤0时，f'（x）＞0在[1，2]上恒成立，
所以f（x）在[1，2]上递增，
所以，解得（舍去），
当a＞0时，由f'（x）＝0，得x＝0或x＝a，
当0＜a≤1时，f'（x）＞0在[1，2]上恒成立，
所以f（x）在[1，2]上递增，
所以，解得（舍去），
当1＜a＜2时，当1＜x＜a时，f'（x）＜0，当a＜x＜2时，f'（x）＞0，
所以f（x）在（1，a）上递减，在（a，2）上递增，
所以当x＝a时，f（x）取得最小值，所以，解得a＝2（舍去），
当a≥2时，当1≤x≤2时，f'（x）＜0，所以f（x）在[1，2]上递减，
所以，解得a＝2，
综上，a＝2，
故选：C．
【变式5-1】（2022春•贵阳期末）若函数在上的最小值为e+1，则a的值为（ ）
A．0B．1C．D．
【解题思路】判断函数f（x）的定义域，可知函数f（x）在定义域上单调递增，由此可建立关于a的方程，解出即可得到答案．
【解答过程】解：函数的定义域为，而函数在[1，+∞）上均为增函数，
∴函数在单调递增，
∴f（x）min＝f（1）＝e+a＝e+1，解得a＝1．
故选：B．
【变式5-2】（2022春•江北区校级期末）若函数f（x）＝x3﹣3x在区间（2a，a+3）上有最小值，则实数a的取值范围是（ ）
A．B．（﹣2，1）C．D．（﹣2，﹣1]
【解题思路】由导数性质得f（x）的增区间是（﹣∞，﹣1），（1，+∞），减区间是（﹣1，1），x＝1时，f（x）min＝﹣2．由此利用函数性质列不等式即可求解a的范围．
【解答过程】解：∵f（x）＝x3﹣3x，∴f′（x）＝3x2﹣3，
由f′（x）＝0，得x＝±1，
x∈（﹣∞，﹣1）时，f′（x）＞0；x∈（﹣1，1）时，f′（x）＜0；x∈（1，+∞）时，f′（x）＞0，
∴f（x）的增区间是（﹣∞，﹣1），（1，+∞），减区间是（﹣1，1），
∴x＝1时，f（x）min＝﹣2．
f（x）＝x3﹣3x＝﹣2时，
x3﹣3x+2＝0，x3﹣x﹣2x+2＝0，
x（x2﹣1）﹣2x+2＝0，
x（x+1）（x﹣1）﹣2（x﹣1）＝0，
（x2+x）（x﹣1）﹣2（x﹣1）＝0，
（x﹣1）（x2+x﹣2）＝0，
（x﹣1）（x+2）（x﹣1）＝0，
（x﹣1）2（x+2）＝0，
解得x＝1，x＝﹣2，
∴﹣2≤2a＜1＜a+3，∴﹣1≤a．
即实数a的取值范围是[﹣1，），
故选：C．
【变式5-3】（2022春•公安县校级月考）已知函数f（x）＝x2eax+1﹣2lnx﹣ax﹣2，若f（x）的最小值为0对任意x＞0恒成立，则实数a的最小值为（ ）
A．B．C．D．
【解题思路】把f（x）转化为f（x）＝e2lnx+ax+1﹣（2lnx+ax+1）﹣1，证明ex﹣1≥x恒成立，得到f（x）≥0恒成立，从而得到a，令g（x），利用导数求出函数g（x）的最小值即可求出结果．
【解答过程】解：∵函数f（x）＝x2eax+1﹣2lnx﹣ax﹣2，
∴，
令t＝lnx2+ax+1，则h（t）＝et﹣t﹣1，f′（t）＝et﹣1，
当t∈（﹣∞，0）时h′（t）＜0，h（t）单调递减，
当t∈（0，+∞）时，h′（t）＞0，h（t）单调递增，
∴h（t）≥h（0）＝0，
∴0，等号成立的条件是lnx2+ax+1＝0，
即在（0，+∞）上有解，
设，则，
令g′（x）＝0，解得，
∴当时，g′（x）＜0，g（x）单调递减，
当时，g′（x）＞0，g（x）单调递增，
∴，即a的最小值为．
故选：A．
【题型6 极值和最值的综合问题】
【方法点拨】
解决函数极值、最值综合问题的策略：
(1)求极值、最值时，要求步骤规范，含参数时，要讨论参数的大小．
(2)求函数最值时，不可想当然地认为极值点就是最值点，要通过比较才能下结论．
(3)函数在给定闭区间上存在极值，一般要将极值与端点值进行比较才能确定最值．
【例6】（2022春•城厢区校级期末）已知函数，其中k∈R．
（1）当k＝3时，求函数f（x）在（0，3）内的极值点；
（2）若函数f（x）在[1，2]上的最小值为3，求实数k的取值范围．
【解题思路】（1）首先求得导函数，然后利用导函数研究函数的单调性，据此可求得函数的值域；
（2）求得函数的解析式，然后结合导函数的符号确定函数的单调性，分类讨论即可求得实数k的取值范围．
【解答过程】解：（1）k＝3时，f（x）＝x3﹣6x2+9x+1，
则f'（x）＝3x2﹣12x+9＝3（x﹣1）（x﹣3），
令f'（x）＝0得x1＝1，x2＝3，
当x＜1时，f′（x）＞0，f（x）单调递增；当1＜x＜3时，f′（x）＜0，f（x）单调递减；当x＞3时，f′（x）＞0，f（x）单调递增；
所以f（x）的单调递增区间为（﹣∞，1），（3，+∞），单调递减区间为（1，3）；
所以f（x）在（0，1）上单调递增，在（1，3）上单调递减．
故f（x）在（0，3）内的极大值点为x＝1，无极小值点；
（2）方法一：f'（x）＝3x2﹣3（k+1）x+3k＝3（x﹣1）（x﹣k），
①当k≤1时，∀x∈[1，2]，f'（x）≥0，
函数f（x）在区间[1，2]单调递增，
所以，
即（舍）；
②当k≥2时，∀x∈[1，2]，f'（x）≤0，
函数f（x）在区间[1，2]单调递减，
所以f（x）min＝f（2）＝8﹣6（k+1）+3k⋅2+1＝3，符合题意；
③当1＜k＜2时，
当x∈[1，k）时，f'（x）≤0，f（x）区间在[1，k）单调递减，
当x∈（k，2]时，f'（x）＞0，f（x）区间在（k，2]单调递减，
所以，
化简得：k3﹣3k2+4＝0，即（k+1）（k﹣2）2＝0，
所以k＝﹣1或k＝2（都舍）；
综上所述：实数k取值范围为k≥2．
【变式6-1】（2022春•德州期末）已知函数．
（1）若函数f（x）在x＝﹣1处取得极值，求实数a的值；
（2）当x∈[﹣2，1]时．求函数f（x）的最大值．
【解题思路】（1）利用导数求得函数极值，代入计算即可得到a的值；
（2）f'（x）＝0的根分类讨论，然后列表表示f'（x）的正负，极值点，同时注意比较端点处函数值，从而得最大值．
【解答过程】解：（1）由题意可知f'（x）＝3x2﹣3a，
因为函数f（x）在x＝﹣1处取得极值，
所以f'（﹣1）＝0，即3﹣3a＝0，解得a＝1，
经检验a＝1，符合题意，
所以a＝1；
（2）由（1）知f'（x）＝3x2﹣3a，
令f'（x）＝0，，
当，即0＜a＜1时，f（x）和f'（x）随x的变化情况如下表：
由表格可知f（x）在x取极大值，此时，
所以f（x）在[﹣2，1]的最大值为．
当，即1≤a＜4时，f（x）和f'（x）随x的变化情况如下表：
由表格可知f（x）在x取极大值，此时，
所以f（x）在[﹣2，1]的最大值为．
当即a≥4时，f'（x）＝3x2﹣3a≤0恒成立，即f（x）在[﹣2，1]上单调递减，所以f（x）的最大值为f（﹣2）＝﹣7+6a，
综上所述，当时，f（x）的最大值为；
当a≥4时，f（x）的最大值为﹣7+6a．
【变式6-2】（2022春•漳州期末）已知函数，f'（x）为f（x）的导函数，函数g（x）＝f'（x）．
（1）当t＝1时，求函数g（x）的最小值；
（2）已知f（x）有两个极值点x1，x2（x1＜x2）且，求实数t的取值范围．
【解题思路】（1）当t＝1时，根据题意可得g（x）＝xex﹣tx﹣2，求导得g'（x）＝（x+1）ex﹣1，分析g（x）的单调性，进而可得g（x）min．
（2）问题可化为，有两个根x1，x2，令，则，求导分析单调性，又x→﹣∞时，h（x）→0；x→+∞时，h（x）→+∞且，推出t＞0且，分析f（x1）的单调性，又，推出﹣1＜x1＜0，即可得出答案．
【解答过程】解：g（x）＝f'（x）＝xex﹣tx﹣2，
（1）当t＝1时，g（x）＝xex﹣x﹣2，g'（x）＝（x+1）ex﹣1，
当x≤﹣1时，x+1≤0，ex＞0，
所以g'（x）＝（x+1）ex﹣1≤0﹣1＜0，
当﹣1＜x＜0时，0＜x+1＜1，0＜ex＜1，
所以g'（x）＝（x+1）ex﹣1＜1×1﹣1＝0，
当x＞0时，x+1＞1，ex＞1，
所以g'（x）＝（x+1）ex﹣1＞1×1﹣1＝0．
综上g（x）在（﹣∞，0）上为减函数，在（0，+∞）上为增函数，
所以g（x）min＝g（0）＝﹣2．
（2）依题有：方程g（x）＝0有两个不同的根x1，x2，
方程g（x）＝0可化为，
令，则，
所以h（x）在（﹣∞，0）和（0，+∞）都是增函数，
因为x→﹣∞时，h（x）→0；x→+∞时，h（x）→+∞且，
所以t＞0且，
所以

，
令，则，
所以φ（x）在（﹣∞，0）上为减函数，又因为，
所以﹣1＜x1＜0，
所以．
【变式6-3】（2022春•潞州区校级期末）有三个条件：
①函数f（x）在x＝1处取得极小值2；
②f（x）在x＝﹣1处取得极大值6；
③函数f（x）的极大值为6，极小值为2．
这三个条件中，请任意选择一个填在下面的横线上（只要填写序号），并解答本题．
题目：已知函数f（x）＝x3﹣3ax+b（a＞0），并且 _____．
（1）求f（x）的解析式；
（2）当x∈[﹣3，1]时，求函数f（x）的最值．
【解题思路】（1）求出函数f（x）的导数f′（x），选择条件①，②，利用给定的极值点及对应的极值列式求解并验证作答；选择条件③，判断极大值与极小值列式求解并验证作答．
（2）利用（1）的结论，利用导数求出给定区间上的最值作答．
【解答过程】解：（1）选条件①：求导得f′（x）＝3x2﹣3a，由，得，
此时f′（x）＝3（x+1）（x﹣1），当﹣1＜x＜1时，f′（x）＜0，当x＞1时，f′（x）＞0，
则f（x）在x＝1处取得极小值2，
所以f（x）＝x3﹣3x+4；
选条件②：求导得f′（x）＝3x2﹣3a，由，得，
此时f′（x）＝3（x+1）（x﹣1），当x＜﹣1时，f′（x）＞0，当﹣1＜x＜1时，f′（x）＝＜0，
则f（x）在x＝﹣1处取得极大值6，
所以f（x）＝x3﹣3x+4．
选条件③：求导得f′（x）＝3x2﹣3a，
令f′（x）＝3x2﹣3a＝0，得x，
当x或x时，f′（x）＞0，当x时时，f′（x）＜0，
因此，当x时，f（x）取得极大值f（），当x时，f（x）取得极小值f（），
于是得，解得，
此时f′（x）＝3（x+1）（x﹣1），当x＜﹣1或x＞1时，f′（x）＞0，当﹣1＜x＜1时，f′（x）＜0，
则f（x）在x＝1处取得极小值2，在x＝﹣1处取得极大值6，
所以f（x）＝x3﹣3x+4；
（2）由（1）知，f（x）＝x3﹣3x+4，当x∈[﹣3，1]时，f′（x）＝3（x+1）（x﹣1），
当﹣3＜x＜﹣1时，f′（x）＞0，当﹣1＜x＜1时，f′（x）＜0，
则f（x）在[﹣3，﹣1）上递增，在（﹣1，1]上递减，
而f（﹣3）＝﹣14，f（1）＝2，
所以f（x）max＝f（﹣1）＝6，f（x）min＝f（﹣3）＝﹣14． 条件
f′(x0)＝0
x0附近的左侧f′(x)>0，右侧f′(x)