高中数学湘教版（2019）选择性必修 第一册第2章 平面解析几何初步2.2 直线的方程课文内容课件ppt

这是一份高中数学湘教版（2019）选择性必修 第一册第2章 平面解析几何初步2.2 直线的方程课文内容课件ppt，共13页。
1.与直线平行、垂直的非零向量分别称为该直线的方向向量、法向量,直线的方 向向量和法向量不唯一.2.斜率为k的直线的方向向量为(1,k)的非零实数倍,直线Ax+By+C=0的法向量可取 (A,B).
2 | 直线的方向向量、法向量
1.方程k= 与y-y0=k(x-x0)表示的意义相同吗?不相同.方程k= 表示的图形中不含点(x0,y0).2.直线y-3=k(x+1)是否恒过定点?是.恒过定点(-1,3).3.直线l在y轴上的截距是直线l与y轴交点到原点的距离吗?不是.直线l在y轴上的截距是直线l与y轴交点的纵坐标,而不是距离.4.直线y=kx+b一定是一次函数y=kx+b的图象吗?不一定.当k≠0时,y=kx+b为一次函数;当k=0时,y=b,不是一次函数,所以只有直线 方程y=kx+b中的k≠0时,该直线才是一次函数的图象.
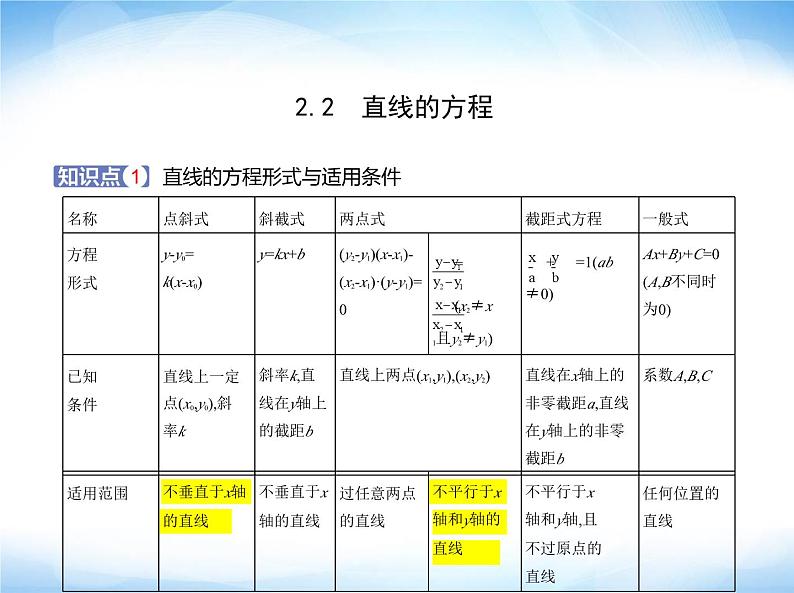
5.直线的点斜式、斜截式、两点式、截距式方程在任何情况下都可以与一般式方程进行互化吗?不是.直线的点斜式、斜截式、两点式、截距式方程均可以化为一般式方程,但 一般式方程转化为其他形式时,必须要在适用范围内.
直线方程的几种常见设法(1)若已知一点的坐标,则一般选用点斜式,再由其他条件确定直线的斜率.(2)若已知直线的斜率,则一般选用斜截式,再由其他条件确定直线在y轴上的截距.(3)若已知两点坐标,则一般选用两点式或点斜式,当两点是直线与坐标轴的交点 时,选用直线的截距式方程.　　无论选用怎样的直线方程,都要注意各自方程的适用范围,对特殊情况下的 直线要单独讨论.
1 直线方程的选择和求解
 典例　写出满足下列条件的直线的方程:(1)经过点(2,-3),倾斜角是直线y= x的倾斜角的2倍;(2)经过点(5,-2),且与y轴平行;(3)过P(-2,3),Q(5,-4)两点;(4)过点A(3,4),且在两坐标轴上的截距互为相反数.
解析    (1)∵直线y= x的斜率为 ,∴直线y= x的倾斜角为30°,∴所求直线的倾斜角为60°,∴所求直线的斜率为 .∴所求直线方程为y+3= (x-2),即 x-y-2 -3=0.(2)与y轴平行的直线,其斜率不存在,但直线上点的横坐标均为5,故直线方程为x= 5.(3)解法一:所求直线方程为 = ,整理得x+y-1=0.解法二:kPQ= = =-1.
∵直线过点P(-2,3),∴所求直线方程为y-3=-(x+2),即x+y-1=0.(4)①当直线在两坐标轴上的截距互为相反数且不为0时,可设直线方程为 + =1.又直线过点A(3,4),所以 + =1,解得a=-1.所以直线方程为 + =1,即x-y+1=0.②当直线在两坐标轴上的截距互为相反数且为0,即直线过原点时,设直线方程为 y=kx,因为直线过点(3,4),
所以4=k·3,解得k= ,所以直线方程为y= x,即4x-3y=0.综上,直线方程为x-y+1=0或4x-3y=0.
易错警示    若题目中出现直线在两坐标轴上的“截距相等”“截距互为相反 数”“在一坐标轴上的截距是另一坐标轴上截距的m(m>0)倍”等条件时,可采用 直线的截距式方程,但一定要注意考虑截距为0的情况.
1.对于含参数的直线方程,可将方程整理成点斜式或斜截式,利用系数的几何意 义,结合图形探求和证明过定点问题.2.根据斜截式中k,b的几何意义,可确定对应函数的大致图象.
2 如何利用直线方程中系数的几何意义解决相关问题
 典例　已知直线l:5ax-5y-a+3=0.(1)求证:无论a为何值,直线l总经过第一象限;(2)为使直线l不经过第二象限,求a的取值范围.
解析    (1)证明:将直线l的方程整理为y- =a ,∴直线l的斜率为a,且过定点 ,设为A,又点A在第一象限,∴无论a为何值,直线l总经过第一象限.(2)由(1),知kOA= =3.如图所示,要使l不经过第二象限,需满足a≥kOA,∴a≥3.