高教版（2021·十四五）拓展模块一（上册）4.1.2 平面的基本性质优秀ppt课件

这是一份高教版（2021·十四五）拓展模块一（上册）4.1.2 平面的基本性质优秀ppt课件，共26页。PPT课件主要包含了探索新知，典型例题，巩固练习，归纳总结，布置作业，情境导入，公理1，公理2，推论1，推论2等内容，欢迎下载使用。

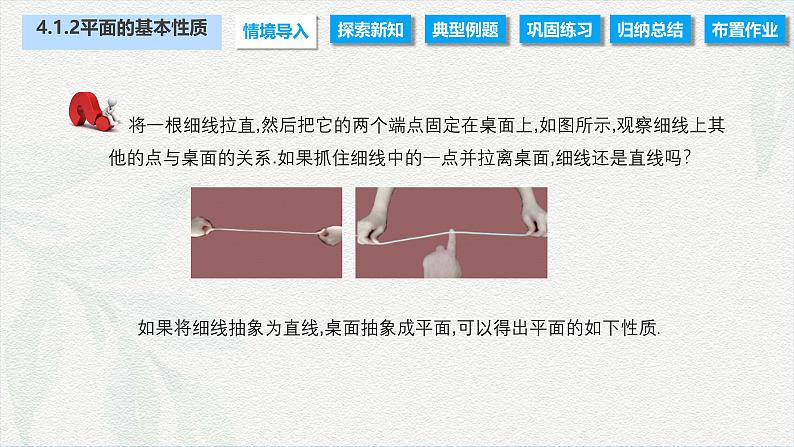
4.1.2平面的基本性质
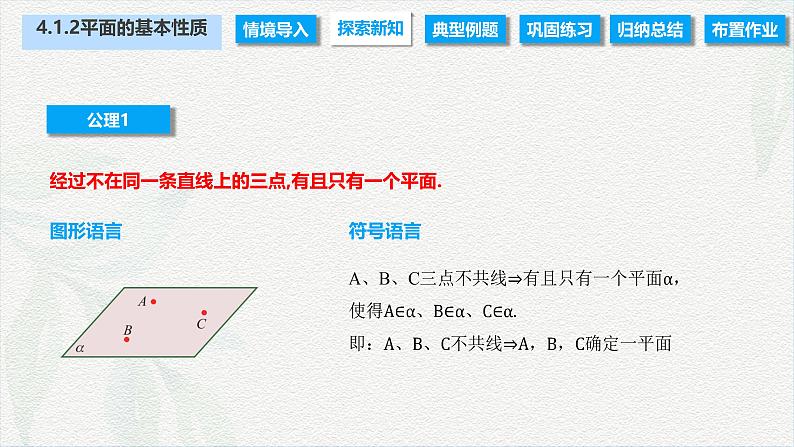
经过不在同一条直线上的三点,有且只有一个平面.
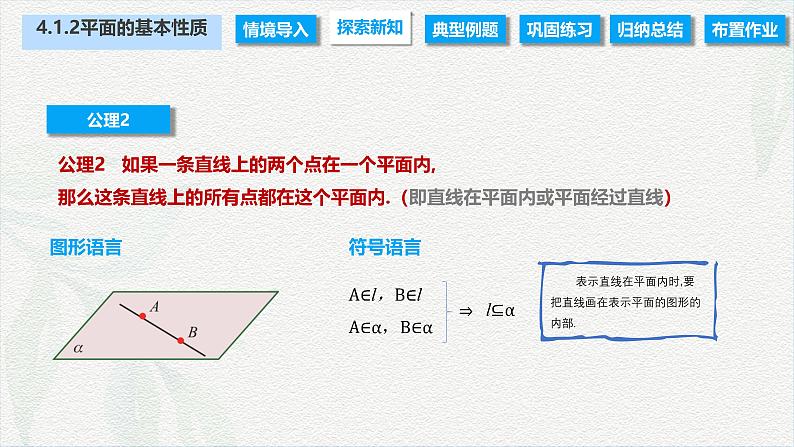
公理2 如果一条直线上的两个点在一个平面内,那么这条直线上的所有点都在这个平面内.（即直线在平面内或平面经过直线）
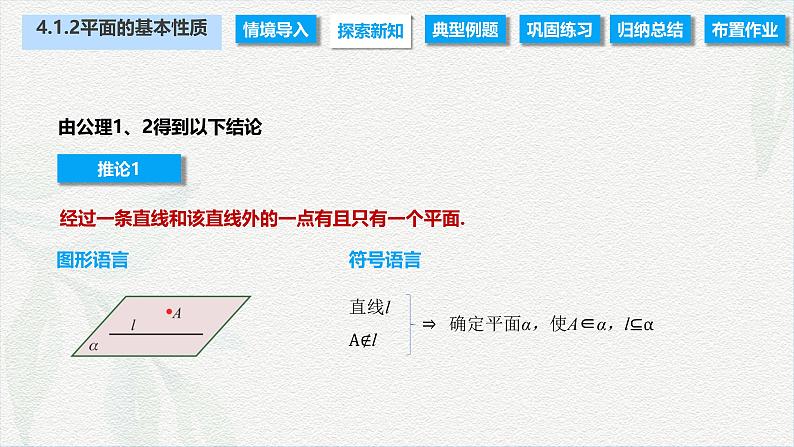
由公理1、2得到以下结论
经过一条直线和该直线外的一点有且只有一个平面. 
经过两条相交直线有且只有一个平面.
经过两条平行直线有且只有一个平面.
如果两个平面有一个公共点,那么它们有且只有一条经过该点的公共直线. 
例2 试用符号语言表示下列语句,并画出相应的图形. （1）点A、B在直线l上,直线l 在平面α内. （2）平面α和平面β相交于直线l.
例3 判断下列说法是否正确.  （1）经过三个点有且只有一个平面； （2）如果直线l与平面α有三个公共点,那么l ⊆α； （3）用三角板的一个顶点与桌面接触,只有一个公共点,故两 个平面可以只有一个公共点.
（2）正确.当一条直线有两个点在平面内时,这条直线就在平面内； 
（3）错误.当两个平面有一个公共点时,这两个平面就有一条经过该点的公共直线,因此它们一定有无数个公共点.
例4 在正方体ABCD-A1B1C1D1[图(1)]中,找出符合下列条件的平面.  （1）经过点A1、B、D的平面； （2）经过直线BC和点D1的平面； （3）经过直线BD和DD1的平面； （4）经过直线AB和C1D1的平面；
1.判断下列说法是否正确. （1）经过直线m和点A的平面有且只有一个；（2）两条相交直线可以确定一个平面； （3）同时经过两条平行直线的平面不止一个； （4）两个平面可以只有一条公共线段. 
 2. 根据平面的基本性质和推论证明平行四边形是平面图形(填空). 已知：四边形 ABCD 是一个平行四边形.求证：AB、BC、CD、DA 四条边共面. 证明：因为 AB∥CD,所以 AB 和CD 确定平面α,如图所示. 因为A∈AB,B∈AB,C∈CD,D∈CD,所以A、B、C、D均在平面α内.从而,有AD⊆ ,BC⊆ , AB⊆ , CD⊆ .所以,AB、BC、CD、DA四条边共面.
3.试用12根长短相等的小木棍(或铁丝等) 制作正方体模型 ABCD-A1B1C1D1, 并指出由顶点A和棱CC1所确定的平面.
由顶点A和棱CC1所确定的平面为AC1
1.书面作业：完成教材第111页习题4.1；2.查漏补缺：根据个人情况对课堂学习复习与回顾;3.拓展作业：阅读教材扩展延伸内容.