



初中数学6.6 余角和补角示范课课件ppt
展开1.理解余角、补角的概念;2.掌握余角、补角的性质,并能运用它们的性质进行角的运算及解决一些实际问题.
生活中处处可见建筑物、道路、桥梁、山川等.在大自然的杰作和人类的创造物中,蕴含着无数的角度.
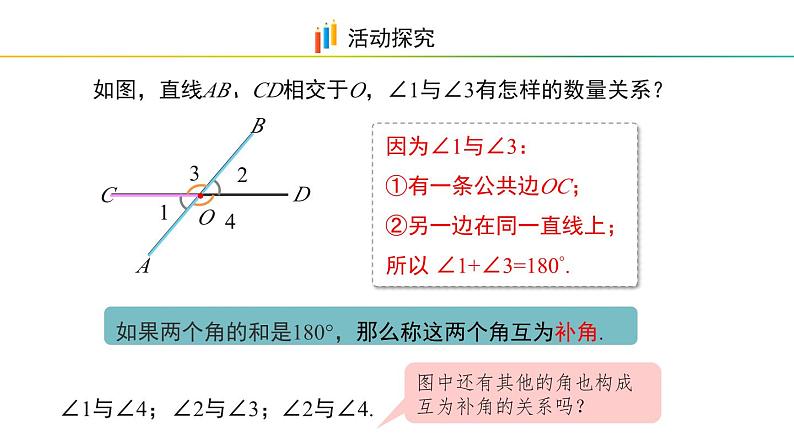
如图,直线AB、CD相交于O,∠1与∠3有怎样的数量关系?
如果两个角的和是180°,那么称这两个角互为补角.
图中还有其他的角也构成互为补角的关系吗?
因为∠1与∠3:①有一条公共边OC;②另一边在同一直线上;所以 ∠1+∠3=180°.
思考:如果两个角的和是90°,那么这两个角有什么关系?
如果两个角的和是90°,那么称这两个角互为余角.
如图:∠1+∠2=90°,所以∠1与∠2互余.
注意:互余与互补是指两个角之间的数量关系,与它们的位置无关.
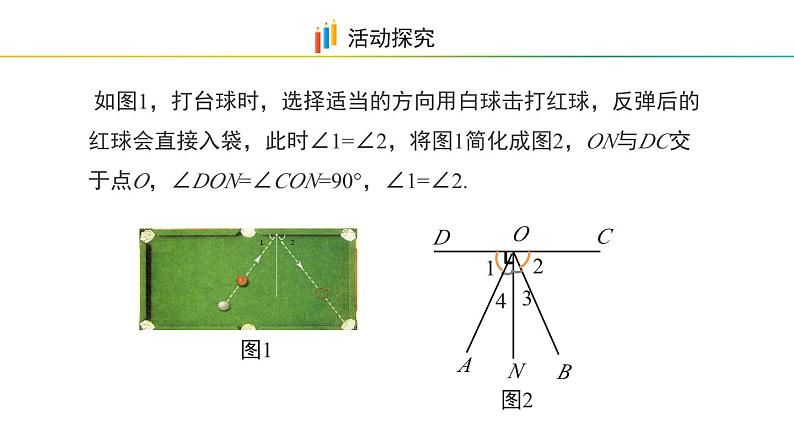
如图1,打台球时,选择适当的方向用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠2,将图1简化成图2,ON与DC交于点O,∠DON=∠CON=90°,∠1=∠2.
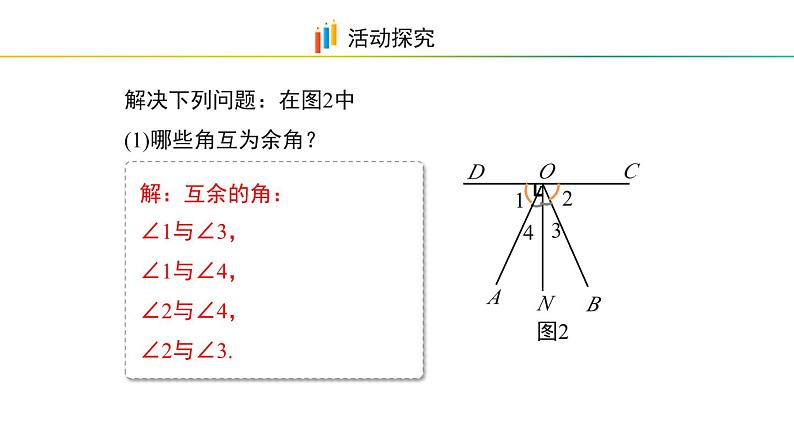
解决下列问题:在图2中(1)哪些角互为余角?
解:互余的角: ∠1与∠3,∠1与∠4,∠2与∠4,∠2与∠3.
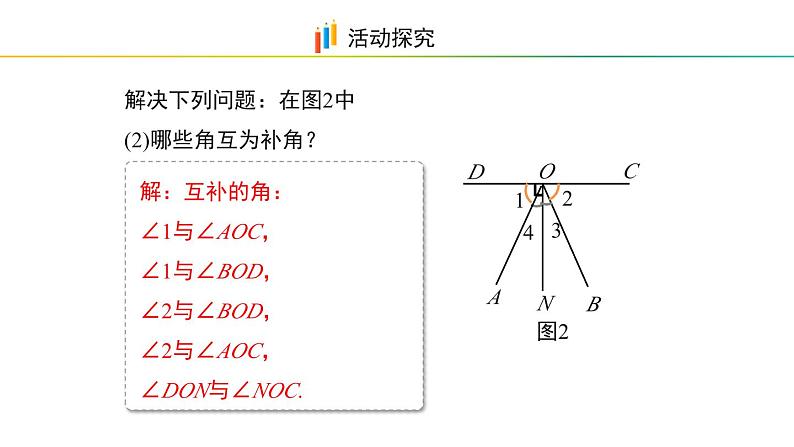
解决下列问题:在图2中(2)哪些角互为补角?
解:互补的角: ∠1与∠AOC, ∠1与∠BOD, ∠2与∠BOD, ∠2与∠AOC, ∠DON与∠NOC.
因为∠1= ∠2,∠ 1+∠3=90°,∠ 2+∠4=90°,所以∠ 3=∠4.
解决下列问题:在图2中(3)∠3与∠4有什么关系?为什么?
同角或等角的余角相等.
因为∠1= ∠2, ∠1+∠AOC=180°, ∠ 2+∠BOD=180°,所以∠AOC=∠BOD.
解:∠AOC=∠BOD,
同角或等角的补角相等.
解决下列问题:在图2中(4)∠AOC与∠BOD有什么关系?为什么?
如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=60°,求∠BOC的度数.
解:因为OA平分∠EOC,∠EOC = 60°,所以∠AOC = 30°,由补角定义,得∠BOC = 180°-∠AOC = 180°- 30° = 150°.
观察可得结论:同一个锐角的补角比它的余角大________.
1.如图已知:直线AB与CD交于点O,∠EOD=90°,回答下列问题:(1)∠AOE的余角是 ;补角是 ; (2)∠AOC的余角是 ;补角是 .
2.如图,直线a、b相交,若∠1 = 40°,求 ∠2的度数.
解:由补角的定义, ∠1 = 40°可得∠2 = 180°-∠1,= 180°- 40°= 140°.
3.若一个角的补角等于它的余角的4 倍,求这个角的度数.
解:设这个角为x度.则它的补角为(180-x)度,它的余角为(90-x)度.根据题意得:180-x=4(90-x),解得: x =60,即这个角为60度.
青岛版(2024)七年级上册6.5 角的比较与运算课堂教学课件ppt: 这是一份青岛版(2024)七年级上册<a href="/sx/tb_c4053887_t3/?tag_id=26" target="_blank">6.5 角的比较与运算课堂教学课件ppt</a>,共19页。PPT课件主要包含了②叠合法,AB=CD,AB>CD,AB<CD,∠ABC>∠DEF,角的比较方法,角的比较,度量法叠合法,角的平分线,差及其计算等内容,欢迎下载使用。
青岛版(2024)七年级上册第6章 基本的几何图形6.3 线段的比较与运算示范课课件ppt: 这是一份青岛版(2024)七年级上册<a href="/sx/tb_c4053885_t3/?tag_id=26" target="_blank">第6章 基本的几何图形6.3 线段的比较与运算示范课课件ppt</a>,共19页。PPT课件主要包含了直接观察难以判断,直接观察,②叠合法,叠合法,解作图步骤如下,解折线AB比较长,解四边形,线段的性质,比较线段的长短,度量法和叠合法等内容,欢迎下载使用。
数学七年级上册6.5 角的比较与运算图文ppt课件: 这是一份数学七年级上册<a href="/sx/tb_c4053887_t3/?tag_id=26" target="_blank">6.5 角的比较与运算图文ppt课件</a>,共1页。













