2025年高考数学一轮复习-10.2-用样本的数字特征估计总体-专项训练【含答案】

这是一份2025年高考数学一轮复习-10.2-用样本的数字特征估计总体-专项训练【含答案】，共6页。试卷主要包含了5　D等内容，欢迎下载使用。

1.若数据x1，x2，…，x9的方差为2，则数据2x1，2x2，…，2x9的方差为（ ）
A.2 B.4
C.6 D.8
2.据某地区气象局发布的气象数据，未来十天内该地区每天最高温度（单位：℃）分别为31，29，24，27，26，25，24，26，26，23，则这组数据的第40百分位数为（ ）
A.27 B.26.5
C.25.5 D.25
3.某校高一年级开设了校本课程，现从甲、乙两班各随机抽取了5名学生校本课程的学分，统计如下表所示，s1，s2分别表示甲、乙两班抽取的5名学生校本课程学分的标准差，则（ ）
A.s1＞s2B.s1＜s2
C.s1＝s2D.s1，s2的大小不能确定
4.某市为了减少水资源的浪费，计划对居民生活用水费用实施阶梯式水价制度.为了确定一个比较合理的标准，通过简单随机抽样，获得了100户居民的月均用水量数据（单位：吨），得到如图所示的频率分布直方图.估计该市居民月均用水量的中位数为（ ）


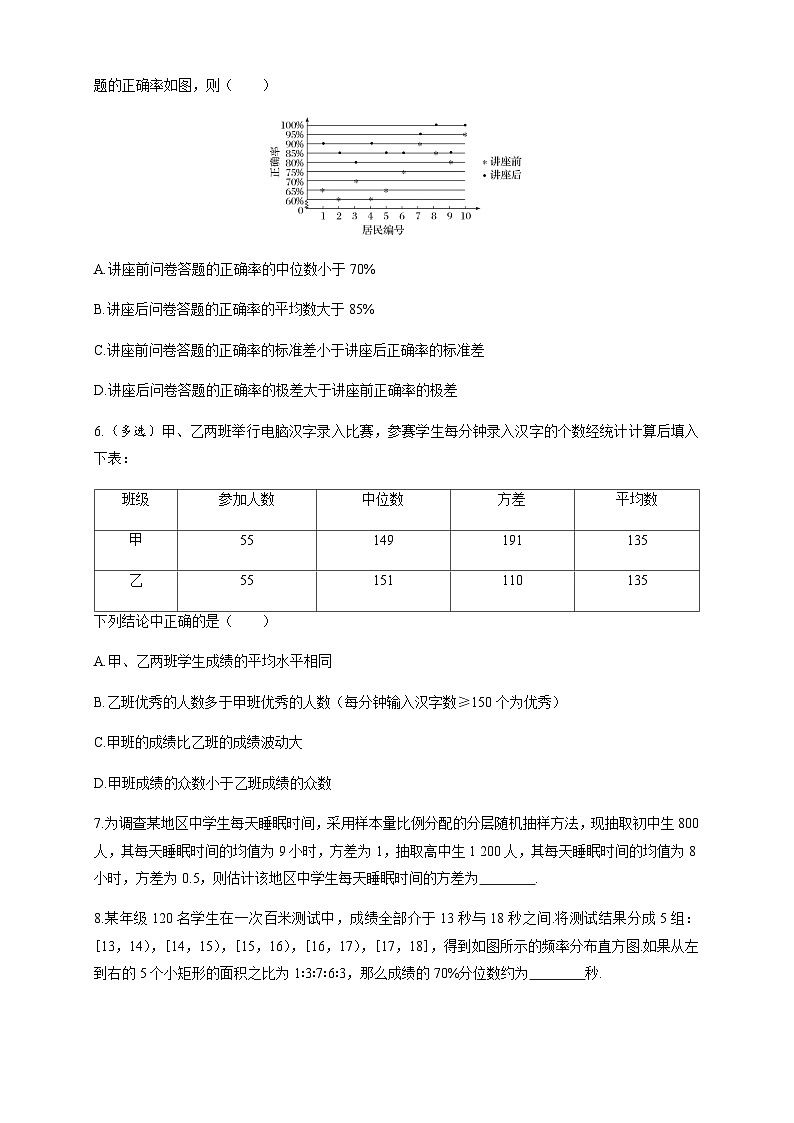
5.某社区通过公益讲座以普及社区居民的垃圾分类知识.为了解讲座效果，随机抽取10位社区居民，让他们在讲座前和讲座后各回答一份垃圾分类知识问卷，这10位社区居民在讲座前和讲座后问卷答题的正确率如图，则（ ）
A.讲座前问卷答题的正确率的中位数小于70%
B.讲座后问卷答题的正确率的平均数大于85%
C.讲座前问卷答题的正确率的标准差小于讲座后正确率的标准差
D.讲座后问卷答题的正确率的极差大于讲座前正确率的极差
6.（多选）甲、乙两班举行电脑汉字录入比赛，参赛学生每分钟录入汉字的个数经统计计算后填入下表：
下列结论中正确的是（ ）
A.甲、乙两班学生成绩的平均水平相同
B.乙班优秀的人数多于甲班优秀的人数（每分钟输入汉字数≥150个为优秀）
C.甲班的成绩比乙班的成绩波动大
D.甲班成绩的众数小于乙班成绩的众数
7.为调查某地区中学生每天睡眠时间，采用样本量比例分配的分层随机抽样方法，现抽取初中生800人，其每天睡眠时间的均值为9小时，方差为1，抽取高中生1 200人，其每天睡眠时间的均值为8小时，方差为0.5，则估计该地区中学生每天睡眠时间的方差为 .
8.某年级120名学生在一次百米测试中，成绩全部介于13秒与18秒之间.将测试结果分成5组：[13，14），[14，15），[15，16），[16，17），[17，18]，得到如图所示的频率分布直方图.如果从左到右的5个小矩形的面积之比为1∶3∶7∶6∶3，那么成绩的70%分位数约为 秒.
9.已知样本x1，x2，…，xn的平均数为x，样本y1，y2，…，ym的平均数为y（x≠y），若样本x1，x2，…，xn，y1，y2，…，ym的平均数z＝ax＋（1－a）y，其中0＜a＜12，则n，m（n，m∈N*）的大小关系为（ ）
A.n＝m B.n≥m
C.n＜m D.n＞m
10.（多选）有一组样本数据x1，x2，…，x6，其中x1是最小值，x6是最大值，则（ ）
A.x2，x3，x4，x5的平均数等于x1，x2，…，x6的平均数
B.x2，x3，x4，x5的中位数等于x1，x2，…，x6的中位数
C.x2，x3，x4，x5的标准差不小于x1，x2，…，x6的标准差
D.x2，x3，x4，x5的极差不大于x1，x2，…，x6的极差
11.气象意义上从春季进入夏季的标志为：“连续5天的日平均温度均不低于22 ℃”，现有甲、乙、丙三地连续5天的日平均温度的记录数据（记录数据都是正整数）：
①甲地：5个数据的中位数为24，众数为22；
②乙地：5个数据的中位数为27，总体均值为24；
③丙地：5个数据中有一个数据是32，总体均值为26，总体方差为10.8.
则肯定进入夏季的地区的序号为 .
12.某种治疗心脏病的中药产品的质量以其质量指标值衡量，质量指标值越大表明质量越好.为了提高中药产品的质量，我国医疗科研专家攻坚克难，研发出A，B两种新配方，在这两种新配方生产的产品中随机抽取数量相同的样本，测量这些产品的质量指标值，规定质量指标值小于85为废品，在[85，115）为一等品，不小于115为特等品.现把测量数据整理如下，其中B配方的样本中有6件废品.
A配方的频数分布表
（1）求实数a，b的值；
（2）试确定A配方和B配方哪一种更好.（说明：在统计方法中，同一组数据常用该组区间的中点值作代表）
参考答案与解析
1.D 根据方差的性质可知，若数据x1，x2，…，x9的方差s2＝2，那么数据2x1，2x2，…，2x9的方差为22s2＝8.
2.C 先将这组数据按照从小到大进行排序，分别为23，24，24，25，26，26，26，27，29，31，又10×40%＝4，所以该组数据的第40百分位数为排序后的第4个数和第5个数的平均数，即25+262＝25.5，故选C.
3.B 甲班抽取的5名学生校本课程学分的平均数x1＝15×（8＋11＋14＋15＋22）＝14，乙班抽取的5名学生校本课程学分的平均数x2＝15×（6＋7＋10＋23＋24）＝14.甲班抽取的5名学生校本课程学分的方差s12＝15×[（8－14）2＋（11－14）2＋（14－14）2＋（15－14）2＋（22－14）2]＝22，∴s1＝22，乙班抽取的5名学生校本课程学分的方差s22＝15×[（6－14）2＋（7－14）2＋（10－14）2＋（23－14）2＋（24－14）2]＝62，∴s2＝62.∴s1＜s2，故选B.
4.B 由频率分布直方图，得月均用水量在5.2吨以下的居民用户所占的比例为4×0.06＝0.24，月均用水量在9.2吨以下的居民用户所占的比例为4×（0.06＋0.08）＝0.56＞0.5，故中位数落在区间[5.2，9.2）内.设样本的中位数为x，则0.24＋（x－5.2）×0.08＝0.5，所以x＝5.2＋0.5－＝8.45，即样本的中位数为8.45，由样本估计总体的思想，估计该市居民月均用水量的中位数为8.45，故选B.
5.B 对于A，讲座前问卷答题的正确率的中位数是70%+75%2＝72.5%，所以A错误；对于B，讲座后问卷答题的正确率分别是80%，85%，85%，85%，85%，90%，90%，95%，100%，100%，其平均数显然大于85%，所以B正确；对于C，由题图可知，讲座前问卷答题的正确率波动较大，讲座后问卷答题的正确率波动较小，所以讲座前问卷答题的正确率的标准差大于讲座后问卷答题的正确率的标准差，所以C错误；对于D，讲座前问卷答题的正确率的极差是95%－60%＝35%，讲座后问卷答题的正确率的极差是100%－80%＝20%，所以讲座前问卷答题的正确率的极差大于讲座后问卷答题的正确率的极差，所以D错误.故选B.
6.ABC 甲、乙两班学生成绩的平均数都是135，故两班学生成绩的平均水平相同，∴A正确；甲、乙两班人数相同，但甲班成绩的中位数为149，乙班成绩的中位数为151，从而易知乙班每分钟输入汉字数≥150个的人数要多于甲班，∴B正确；s甲2＝191＞110＝s乙2，∴甲班成绩不如乙班稳定，即甲班成绩波动较大，∴C正确；由题表看不出两班学生成绩的众数，∴D不正确.故选A、B、C.
解析：该地区中学生每天睡眠时间的平均数为800×9+1 200×81 200+800＝8.4（小时），则该地区中学生每天睡眠时间的方差为8001 200+800×[1＋（9－8.4）2]＋1 2001 200+800×[0.5＋（8－8.4）2]＝0.94.
8.16.5 解析：因为1+3+71+3+7+6+3＝0.55＝55%，1+3+7+61+3+7+6+3＝0.85＝85%，所以70%分位数在[16，17）内，所以70%分位数约为16＋0.7－－0.55＝16.5（秒）.
9.C 由题意得z＝1n＋m（nx＋my）＝nn＋mx＋1－nn＋my，∴a＝nn＋m，∵0＜a＜12，∴0＜nn＋m＜12，又n，m∈N*，∴2n＜n＋m，∴n＜m.故选C.
10.BD 若该组样本数据为1，2，3，4，5，8，则2，3，4，5的平均数为72，1，2，3，4，5，8的平均数为236，两组数据的平均数不相等，故A错误；不妨设x1≤x2≤x3≤x4≤x5≤x6，则x2，x3，x4，x5的中位数等于x1，x2，x3，x4，x5，x6的中位数，故B正确；若该组样本数据为1，2，2，2，2，8，则2，2，2，2的标准差为0，而1，2，2，2，2，8的标准差大于0，故C错误；由对选项B的分析可知，x2，x3，x4，x5的极差为x5－x2，x1，x2，x3，x4，x5，x6的极差为x6－x1，且易得x6－x1≥x5－x2，故D正确.故选B、D.
11.①③ 解析：由统计知识，①甲地：5个数据的中位数为24，众数为22，可知①符合题意；②乙地：5个数据的中位数为27，总体均值为24，当5个数据为19，20，27，27，27，可知其不满足连续5天的日平均温度不低于22 ℃，所以不符合题意；③丙地：5个数据中有一个数据是32，总体均值为26，总体方差为10.8.若某一天的气温低于22 ℃，此时可取21 ℃，总体方差就大于10.8.所以满足题意.
12.解：（1）依题意，A，B两种配方的样本容量相同，设为n.
由B配方的样本中有6件废品，结合B配方的频率分布直方图，得6n＝0.006×10，解得n＝100.
∴a＝100－（8＋36＋24＋8）＝24.
由（0.006＋b＋0.038＋0.022＋0.008）×10＝1，得b＝0.026.
∴实数a，b的值分别为24，0.026.
（2）由（1）及A配方的频数分布表得，A配方质量指标值的样本平均数xA＝1100×（80×8＋90×24＋100×36＋110×24＋120×8）＝1100×（200×8＋200×24＋100×36）＝100，
A配方质量指标值的样本方差sA2＝1100×[（－20）2×8＋（－10）2×24＋0×36＋102×24＋202×8]＝112.
由（1）及B配方的频率分布直方图得，B配方质量指标值的样本平均数xB＝80×0.06＋90×0.26＋100×0.38＋110×0.22＋120×0.08＝100，
B配方质量指标值的样本方差sB2＝（－20）2×0.06＋（－10）2×0.26＋0×0.38＋102×0.22＋202×0.08＝104.
综上，xA＝xB，sA2＞sB2，
即A，B两种配方质量指标值的样本平均数相等，但A配方质量指标值没有B配方质量指标值稳定，
∴B配方更好.
甲
8
11
14
15
22
乙
6
7
10
23
24
班级
参加人数
中位数
方差
平均数
甲
55
149
191
135
乙
55
151
110
135
质量指标值
[75，85）
[85，95）
[95，105）
[105，115）
[115，125]
频数
8
a
36
24
8