2025高考数学一轮复习- 用样本的数字特征估计总体-专项训练【含解析】

这是一份2025高考数学一轮复习- 用样本的数字特征估计总体-专项训练【含解析】，共11页。


1．数据1,2,3,4,5,6的60%分位数为( )
A．3 B．3．5
C．3．6D．4
2．若数据x1，x2，…，xn的平均数为 eq \(x,\s\up6(－))，方差为s2，则2x1＋3,2x2＋3，…，2xn＋3的平均数和方差分别为( )
A．eq \(x,\s\up6(－))和s2B．2eq \(x,\s\up6(－))＋3和4s2
C．2eq \(x,\s\up6(－))＋3和s2D．2eq \(x,\s\up6(－))＋3和4s2＋12s＋9
3．为了反映各行业对仓储物流业务需求变化的情况，以及重要商品库存变化的动向，中国物流与采购联合会和中储发展股份有限公司通过联合调查，制定了中国仓储指数．由2019年1月至2020年7月的调查数据得出的中国仓储指数，绘制出如下折线图．
根据该折线图，下列结论正确的是( )
A．2019年各月的仓储指数最大值是在3月份
B．2020年1月至7月的仓储指数的中位数为55
C．2020年1月与4月的仓储指数的平均数为52
D．2019年1月至4月的仓储指数相对于2020年1月至4月，波动性更大
4．已知样本甲：x1，x2，x3，…，xn与样本乙：y1，y2，y3，…，yn，满足yi＝2xeq \\al(3,i)＋1(i＝1,2，…，n)，则下列叙述中一定正确的是( )
A．样本乙的极差等于样本甲的极差
B．样本乙的众数大于样本甲的众数
C．若某个xi为样本甲的中位数，则yi是样本乙的中位数
D．若某个xi为样本甲的平均数，则yi是样本乙的平均数
5．已知样本x1，x2，…，xn的平均数为x，样本y1，y2，…，ym的平均数为y(x≠y)，若样本x1，x2，…，xn，y1，y2，…，ym的平均数z＝ax＋(1－a)y，其中0＜a＜eq \f(1,2)，则n，m(n，m∈N*)的大小关系为( )
A．n＝mB．n≥m
C．n＜mD．n＞m
6．(多选)甲、乙两班举行电脑汉字录入比赛，参赛学生每分钟录入汉字的个数经统计计算后填入下表：
下列结论中，正确的是( )
A．甲、乙两班学生成绩的平均水平相同
B．乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字数≥150个为优秀)
C．甲班的成绩波动情况比乙班的成绩波动大
D．甲班成绩的众数小于乙班成绩的众数
7．(多选)某篮球爱好者在一次篮球训练中，需进行五轮投篮，每轮投篮5次．统计各轮投进球的个数，获知其前四轮投中的个数分别为2,3,4,4，则第五轮结束后，下列数字特征有可能发生的是( )
A．平均数为3，极差是3
B．中位数是3，极差是3
C．平均数为3，方差是0．8
D．中位数是3，方差是0．56
8．已知一组数据按从小到大的顺序排列，得到－1,0,4，x,7,14，中位数为5，则这组数据的平均数为________，方差为_________．
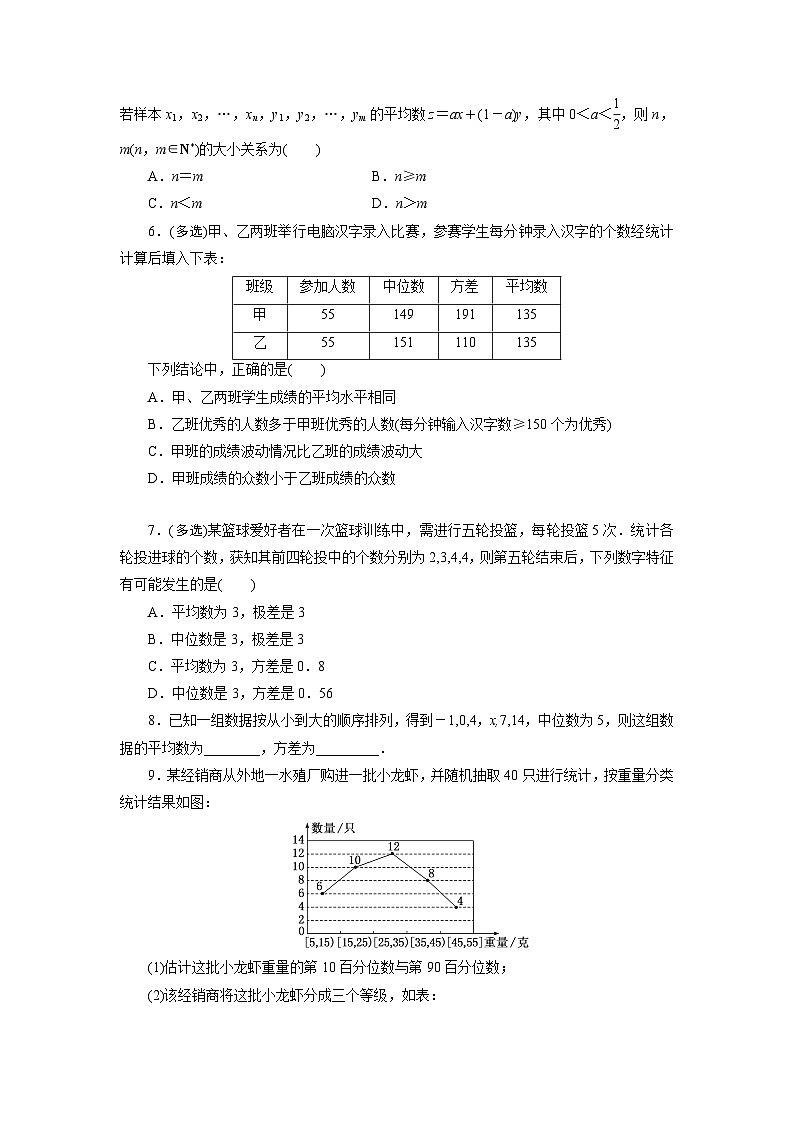
9．某经销商从外地一水殖厂购进一批小龙虾，并随机抽取40只进行统计，按重量分类统计结果如图：
(1)估计这批小龙虾重量的第10百分位数与第90百分位数；
(2)该经销商将这批小龙虾分成三个等级，如表：
试估计这批小龙虾划为几等品比较合理？
10．(多选)2020年2月8日，在韩国首尔举行的四大洲花样滑冰锦标赛双人自由滑比赛中，中国组合隋文静/韩聪以总分217．51分拿下四大洲赛冠军，这也是他们第六次获得四大洲冠军．中国另一对组合彭程/金杨以213．29分摘得银牌．花样滑冰锦标赛有9位评委进行评分，首先这9位评委给出某对选手的原始分数，评定该队选手的成绩时从9个原始评分中去掉一个最高分、一个最低分，得到7个有效评分，则7个有效评分与9个原始评分相比，可能变化的数字特征是( )
A．中位数B．平均数
C．方差D．极差
11．(多选)随着人民生活水平的提高，对城市空气质量的关注度也逐步增大，如图是某城市1月至8月的空气质量检测情况，图中一、二、三、四级是空气质量等级，一级空气质量最好，一级和二级都是质量合格天气，下面四种说法正确的是( )
A．1月至8月空气质量合格天数超过20天的月份有5个
B．第二季度与第一季度相比，空气质量合格天数的比重下降了
C．8月是空气质量最好的一个月
D．6月的空气质量最差
12．某快递网点收取快递费用的标准是重量不超过1 kg的包裹收费10元，重量超过1 kg的包裹，除收费10元之外，超过1 kg的部分，每超出1 kg(不足1 kg，按1 kg计算)需要再收费5元．该公司近60天每天揽件数量的频率分布直方图如图所示(同一组数据用该区间的中点值作代表)．
(1)求这60天每天包裹数量的平均数和中位数；
(2)该快递网点负责人从收取的每件快递的费用中抽取5元作为工作人员的工资和网点的利润，剩余的作为其他费用．已知该网点有工作人员3人，每人每天工资100元，以样本估计总体，试估计该网点每天的利润有多少元？
13．记样本x1，x2，…，xm的平均数为eq \(x,\s\up6(－))，样本y1，y2，…，yn的平均数为eq \(y,\s\up6(－))(eq \(x,\s\up6(－))≠eq \(y,\s\up6(－)))．若样本x1，x2，…，xm，y1，y2，…，yn的平均数为eq \(z,\s\up6(－))＝eq \f(1,4)eq \(x,\s\up6(－))＋eq \f(3,4)eq \(y,\s\up6(－))，则eq \f(m,n)的值为( )
A．3B．4
C．eq \f(1,4)D．eq \f(1,3)
14．某校有高中生2 000人，其中男女生比例约为5∶4，为了获得该校全体高中生的身高信息，采取了以下两种方案：方案一：采用比例分配的分层随机抽样方法，抽收了样本量为n的样本，得到如图所示的频数分布表和频率分布直方图．方案二：采用分层随机抽样方法，抽取了男、女生样本量均为25的样本，计算得到男生样本的均值为170，方差为16，女生样本的均值为160，方差为20．
(1)根据图表信息，求n，q并补充完整频率分布直方图，估计该校高中生的身高均值；(同一组中的数据以这组数据所在区间中点的值为代表)
(2)计算方案二中总样本的均值及方差；
(3)计算两种方案总样本均值的差，并说明用方案二总样本的均值作为总体均值的估计合适吗？为什么？
课时过关检测(六十五)
用样本的数字特征估计总体【解析版】
1．数据1,2,3,4,5,6的60%分位数为( )
A．3 B．3．5
C．3．6D．4
解析：D 由6×60%＝3．6，所以数据1,2,3,4,5,6的60%分位数是第四个数，故选D．
2．若数据x1，x2，…，xn的平均数为 eq \(x,\s\up6(－))，方差为s2，则2x1＋3,2x2＋3，…，2xn＋3的平均数和方差分别为( )
A．eq \(x,\s\up6(－))和s2B．2eq \(x,\s\up6(－))＋3和4s2
C．2eq \(x,\s\up6(－))＋3和s2D．2eq \(x,\s\up6(－))＋3和4s2＋12s＋9
解析：B 原数据乘以2加上3得到一组新数据，则由平均数、方差的性质可知得到的新数据的平均数和方差分别是2eq \(x,\s\up6(－))＋3和4s2．
3．为了反映各行业对仓储物流业务需求变化的情况，以及重要商品库存变化的动向，中国物流与采购联合会和中储发展股份有限公司通过联合调查，制定了中国仓储指数．由2019年1月至2020年7月的调查数据得出的中国仓储指数，绘制出如下折线图．
根据该折线图，下列结论正确的是( )
A．2019年各月的仓储指数最大值是在3月份
B．2020年1月至7月的仓储指数的中位数为55
C．2020年1月与4月的仓储指数的平均数为52
D．2019年1月至4月的仓储指数相对于2020年1月至4月，波动性更大
解析：D 2019年各月的仓储指数最大值是在11月份，所以A错误；由题图可知，2020年1月至7月的仓储指数的中位数约为53，所以B错误；2020年1月与4月的仓储指数的平均数约为eq \f(51＋55,2)＝53，所以C错误；由题图可知，2019年1月至4月的仓储指数比2020年1月至4月的仓储指数波动更大，故选D．
4．已知样本甲：x1，x2，x3，…，xn与样本乙：y1，y2，y3，…，yn，满足yi＝2xeq \\al(3,i)＋1(i＝1,2，…，n)，则下列叙述中一定正确的是( )
A．样本乙的极差等于样本甲的极差
B．样本乙的众数大于样本甲的众数
C．若某个xi为样本甲的中位数，则yi是样本乙的中位数
D．若某个xi为样本甲的平均数，则yi是样本乙的平均数
解析：C ∵yi＝2xeq \\al(3,i)＋1，∴yi关于xi单调递增，甲样本极差为xn－x1，乙样本极差为yn－y1＝2(xeq \\al(3,n)－xeq \\al(3,1))＝2(xn－x1)(xeq \\al(2,n)＋xnx1＋xeq \\al(2,1))，两个数据大小关系不定，∴样本乙的极差不一定等于样本甲的极差，A错误；样本乙的众数不一定大于样本甲的众数，B错误；若xi为样本甲的平均数，yi不一定是样本乙的平均数，D错误；若xi为样本甲的中位数时，则yi一定是样本乙的中位数，C正确．
5．已知样本x1，x2，…，xn的平均数为x，样本y1，y2，…，ym的平均数为y(x≠y)，若样本x1，x2，…，xn，y1，y2，…，ym的平均数z＝ax＋(1－a)y，其中0＜a＜eq \f(1,2)，则n，m(n，m∈N*)的大小关系为( )
A．n＝mB．n≥m
C．n＜mD．n＞m
解析：C 由题意得z＝eq \f(1,n＋m)(nx＋my)＝eq \f(n,n＋m)x＋eq \b\lc\(\rc\)(\a\vs4\al\c1(1－\f(n,n＋m)))y，∴a＝eq \f(n,n＋m)，∵0＜a＜eq \f(1,2)，∴0＜eq \f(n,n＋m)＜eq \f(1,2)，又n，m∈N*，∴2n＜n＋m，∴n＜m．故选C．
6．(多选)甲、乙两班举行电脑汉字录入比赛，参赛学生每分钟录入汉字的个数经统计计算后填入下表：
下列结论中，正确的是( )
A．甲、乙两班学生成绩的平均水平相同
B．乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字数≥150个为优秀)
C．甲班的成绩波动情况比乙班的成绩波动大
D．甲班成绩的众数小于乙班成绩的众数
解析：ABC 甲、乙两班成绩的平均数都是135，故两班成绩的平均水平相同，∴A正确；seq \\al(2,甲)＝191＞110＝seq \\al(2,乙)，∴甲班成绩不如乙班稳定，即甲班成绩波动较大，∴C正确；甲、乙两班人数相同，但甲班成绩的中位数为149，乙班成绩的中位数为151，从而易知乙班每分钟输入汉字数≥150个的人数要多于甲班，∴B正确；由题表看不出两班学生成绩的众数，∴D错误．
7．(多选)某篮球爱好者在一次篮球训练中，需进行五轮投篮，每轮投篮5次．统计各轮投进球的个数，获知其前四轮投中的个数分别为2,3,4,4，则第五轮结束后，下列数字特征有可能发生的是( )
A．平均数为3，极差是3
B．中位数是3，极差是3
C．平均数为3，方差是0．8
D．中位数是3，方差是0．56
解析：BCD 2＋3＋4＋4＝13，①若平均数为3，则第五轮投中的个数为2，所以极差为4－2＝2，方差为eq \f(1,5)×[(2－3)2×2＋(3－3)2＋(4－3)2×2]＝0．8，即选项A错误，C正确；
②若中位数为3，则第五轮投中的个数为0或1或2或3，
当投中的个数为0时，极差为4，平均数为2．6，方差为eq \f(1,5)×[(0－2．6)2＋(2－2．6)2＋(3－2．6)2＋(4－2．6)2×2]＝2．24；
当投中的个数为1时，极差为3，平均数为2．8，方差为eq \f(1,5)×[(1－2．8)2＋(2－2．8)2＋(3－2．8)2＋(4－2．8)2×2]＝1．36；
当投中的个数为2时，极差为2，方差为0．8；
当投中的个数为3时，极差为2，平均数为3．2，方差为eq \f(1,5)×[(2－3．2)2＋(3－3．2)2×2＋(4－3．2)2×2]＝0．56，即选项B和D均正确．故选B、C、D．
8．已知一组数据按从小到大的顺序排列，得到－1,0,4，x,7,14，中位数为5，则这组数据的平均数为________，方差为_________．
解析：∵－1,0,4，x,7,14的中位数为5，∴eq \f(4＋x,2)＝5，∴x＝6，∴这组数据的平均数是eq \f(－1＋0＋4＋6＋7＋14,6)＝5，这组数据的方差是eq \f(1,6)×(36＋25＋1＋1＋4＋81)＝eq \f(74,3)．
答案：5 eq \f(74,3)
9．某经销商从外地一水殖厂购进一批小龙虾，并随机抽取40只进行统计，按重量分类统计结果如图：
(1)估计这批小龙虾重量的第10百分位数与第90百分位数；
(2)该经销商将这批小龙虾分成三个等级，如表：
试估计这批小龙虾划为几等品比较合理？
解：(1)因为40×10% ＝4，所以第10百分位数为第4项与第5项的平均数，在[5,15)范围内约为eq \f(5＋15,2)＝10．
因为40×90%＝36，所以第90百分位数为第36项与第37项的平均数，在[35,55]范围内，约为eq \f(35＋55,2)＝45，
所以估计这批小龙虾重量的第10百分位数为10，第90百分位数为45．
(2)由(1)知，这批小龙虾重量集中在[10,45]范围内，所以划为二等品比较合理．
10．(多选)2020年2月8日，在韩国首尔举行的四大洲花样滑冰锦标赛双人自由滑比赛中，中国组合隋文静/韩聪以总分217．51分拿下四大洲赛冠军，这也是他们第六次获得四大洲冠军．中国另一对组合彭程/金杨以213．29分摘得银牌．花样滑冰锦标赛有9位评委进行评分，首先这9位评委给出某对选手的原始分数，评定该队选手的成绩时从9个原始评分中去掉一个最高分、一个最低分，得到7个有效评分，则7个有效评分与9个原始评分相比，可能变化的数字特征是( )
A．中位数B．平均数
C．方差D．极差
解析：BCD 因为7个有效评分是9个原始评分中去掉一个最高分、一个最低分，所以中位数不变，平均数、方差、极差可能发生变化，所以可能变化的数字特征是平均数、方差、极差，故选B、C、D．
11．(多选)随着人民生活水平的提高，对城市空气质量的关注度也逐步增大，如图是某城市1月至8月的空气质量检测情况，图中一、二、三、四级是空气质量等级，一级空气质量最好，一级和二级都是质量合格天气，下面四种说法正确的是( )
A．1月至8月空气质量合格天数超过20天的月份有5个
B．第二季度与第一季度相比，空气质量合格天数的比重下降了
C．8月是空气质量最好的一个月
D．6月的空气质量最差
解析：ABC 1月至8月空气质量合格天数超过20天的月份有：1月，2月，6月，7月，8月，共5个，所以A是正确的；第一季度合格天数的比重为eq \f(22＋26＋19,31＋29＋31)≈0．736 3，第二季度合格天数的比重为eq \f(19＋13＋25,30＋31＋30)≈0．626 4，所以第二季度与第一季度相比，空气质量合格的天数的比重下降了，所以B是正确的；8月空气质量合格天气达到30天，是空气质量最好的一个月，所以C是正确的；5月空气质量合格天气只有13天，5月份的空气质量最差，所以D是错误的，故选A、B、C．
12．某快递网点收取快递费用的标准是重量不超过1 kg的包裹收费10元，重量超过1 kg的包裹，除收费10元之外，超过1 kg的部分，每超出1 kg(不足1 kg，按1 kg计算)需要再收费5元．该公司近60天每天揽件数量的频率分布直方图如图所示(同一组数据用该区间的中点值作代表)．
(1)求这60天每天包裹数量的平均数和中位数；
(2)该快递网点负责人从收取的每件快递的费用中抽取5元作为工作人员的工资和网点的利润，剩余的作为其他费用．已知该网点有工作人员3人，每人每天工资100元，以样本估计总体，试估计该网点每天的利润有多少元？
解：(1)每天包裹数量的平均数为0．1×50＋0．1×150＋0．5×250＋0．2×350＋0．1×450＝260(件)，
因为[0,200)的频率为0．2，[200,300)的频率为0．5，
中位数为200＋ eq \f(0.5－0.2,0.5)×100＝260(件)，
所以该网点每天包裹的平均数和中位数都为260件．
(2)由(1)可知平均每天的揽件数为260件，
利润为260×5－3×100＝1 000(元)，
所以该网点平均每天的利润有1 000元．
13．记样本x1，x2，…，xm的平均数为eq \(x,\s\up6(－))，样本y1，y2，…，yn的平均数为eq \(y,\s\up6(－))(eq \(x,\s\up6(－))≠eq \(y,\s\up6(－)))．若样本x1，x2，…，xm，y1，y2，…，yn的平均数为eq \(z,\s\up6(－))＝eq \f(1,4)eq \(x,\s\up6(－))＋eq \f(3,4)eq \(y,\s\up6(－))，则eq \f(m,n)的值为( )
A．3B．4
C．eq \f(1,4)D．eq \f(1,3)
解析：D 由题意知x1＋x2＋…＋xm＝meq \(x,\s\up6(－))，y1＋y2＋…＋yn＝neq \(y,\s\up6(－))，eq \(z,\s\up6(－))＝eq \f(x1＋x2＋…＋xm＋y1＋y2＋…＋yn,m＋n)＝eq \f(m\(x,\s\up6(－))＋n\(y,\s\up6(－)),m＋n)＝eq \f(m\(x,\s\up6(－)),m＋n)＋eq \f(n\(y,\s\up6(－)),m＋n)＝eq \f(1,4)eq \(x,\s\up6(－))＋eq \f(3,4)eq \(y,\s\up6(－))，所以eq \f(m,m＋n)＝eq \f(1,4)，eq \f(n,m＋n)＝eq \f(3,4)，可得3m＝n，所以eq \f(m,n)＝eq \f(1,3)．
14．某校有高中生2 000人，其中男女生比例约为5∶4，为了获得该校全体高中生的身高信息，采取了以下两种方案：方案一：采用比例分配的分层随机抽样方法，抽收了样本量为n的样本，得到如图所示的频数分布表和频率分布直方图．方案二：采用分层随机抽样方法，抽取了男、女生样本量均为25的样本，计算得到男生样本的均值为170，方差为16，女生样本的均值为160，方差为20．
(1)根据图表信息，求n，q并补充完整频率分布直方图，估计该校高中生的身高均值；(同一组中的数据以这组数据所在区间中点的值为代表)
(2)计算方案二中总样本的均值及方差；
(3)计算两种方案总样本均值的差，并说明用方案二总样本的均值作为总体均值的估计合适吗？为什么？
解：(1)因为身高在区间[185,195]的频率为0．008×10＝0．08，频数为4，
所以样本量n＝eq \f(4,0.08)＝50，m＝0．008×10×50＝4，p＝0．04×10×50＝20，q＝50－4－20－6－4＝16，
所以身高在[165,175)的频率为eq \f(16,50)＝0．32，小矩形的高为0．032，
所以身高在[175,185)的频率为eq \f(6,50)＝0．12，小矩形的高为0．012，
由此补全频率分布直方图：
由频率分布直方图可知样本的身高均值为(150×0．008＋160×0．04＋170×0．032＋180×0．012＋190×0．008)×10＝167．2，
所以由样本估计总体可知，估计该校高中生的身高均值为167．2．
(2)把男生样本记为x1，x2，x3，…，x25，其均值为eq \(x,\s\up6(－))，方差为seq \\al(2,x)，
把女生样本记为y1，y2，y3，…，y25，其均值为eq \(y,\s\up6(－))，方差为seq \\al(2,y)，
总体样本均值记为eq \(z,\s\up6(－))，方差记为s2，
所以eq \(z,\s\up6(－))＝eq \f(25,25＋25)eq \(x,\s\up6(－))＋eq \f(25,25＋25)eq \(y,\s\up6(－))＝eq \f(25×170＋25×160,50)＝165，
s2＝eq \f(1,50)eq \b\lc\{\rc\}(\a\vs4\al\c1(25[s\\al(2,x)＋\(x,\s\up6(－))－\(z,\s\up6(－))2]＋25[s\\al(2,y)＋\(y,\s\up6(－))－\(z,\s\up6(－))2]))＝eq \f(1,50){25[16＋(170－165)2]＋25[20＋(160－165)2]}＝43．
(3)两种方案总样本均值的差为167．2－165＝2．2，所以用方案二总体样本均值作为总体均值的估计不合适，原因是没有进行等比例的分层随机抽样，每个个体被抽到的可能性不同，因此代表性较差．
班级
参加人数
中位数
方差
平均数
甲
55
149
191
135
乙
55
151
110
135
等级
三等品
二等品
一等品
重量/克
[5,25)
[25,45)
[45,55]
身高(单
位：cm)
[145，
155)
[155，
165)
[165，
175)
[175，
185)
[185，
195]
频数
m
p
q
6
4
班级
参加人数
中位数
方差
平均数
甲
55
149
191
135
乙
55
151
110
135
等级
三等品
二等品
一等品
重量/克
[5,25)
[25,45)
[45,55]
身高(单
位：cm)
[145，
155)
[155，
165)
[165，
175)
[175，
185)
[185，
195]
频数
m
p
q
6
4