






还剩19页未读,
继续阅读
成套系列资料,整套一键下载
北师大数学六年级上册 第5单元《数据处理》单元热点难点课件
展开
这是一份北师大数学六年级上册 第5单元《数据处理》单元热点难点课件,共27页。
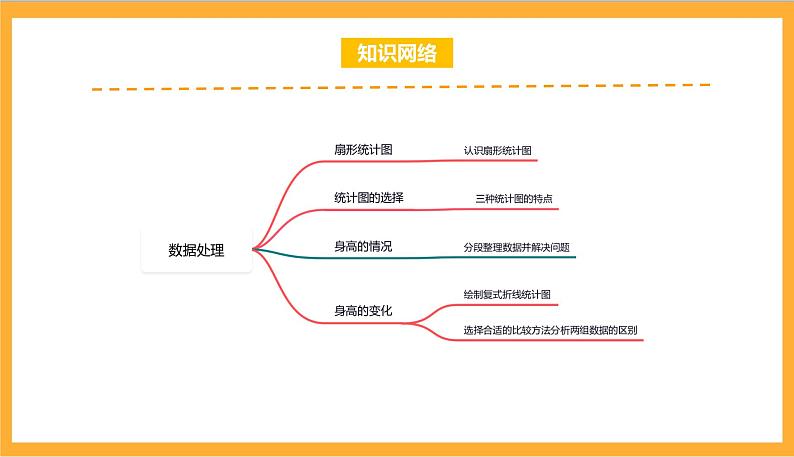
北师大数学六年级上册 第五单元《数据处理》单元热点难点知识网络扇形统计图是用整个圆的面积表示总数量,用圆内各扇形的面积表示各部分数量占总数量的百分比。知识梳理要正确选择合适的统计图进行统计,首先要掌握三种统计图的不同特点,再根据不同的特点结合实际情况在反复实践中加强对比,这样才能选择合适的统计图。在分组整理数据时,要根据实际情况来确定每一段的数量,以便清楚地表达信息。在同等情况下,折线越陡,数量变化越大,反之,数量变化越小。分析典例01(1)由题意可知,把全校参加活动人数看作单位“1”,根据六年级参加活动的36人是全校参加活动总人数的18%,可用“36÷18%求出全校参加活动的总人数;(2)分别用全参加活动的总人数乘三年级和四年级对应的百分率,就可求出三年级的四年级参加活动的人数,再写成比的形式并化简;(3)不能,因为一二年级参加活动的人数共占全校参加活动总人数的32%,有可能其中一个年级占的百分率比五年级多。学校开展劳动教育实践活动。数学统计小组对各年级同学参加活动人数情况做了调查,并绘制了扇形统计图。请你根据图中提供的信息,解答下列问题。(1)六年级有36人参加活动,全校共有 人参加活动。(2)三年级和四年级参加活动人数的比是 : 。(3)从这幅统计图中能否得出“五年级参加活动人数最多”的结论?请说明理由。精讲精练点评解答解决本题关键是从图中读出数据,找出单位“1”,再根据基本的数量关系求解。解:(1)36÷18%=36÷0.18=200(人)答:全校有200人参加活动。(2)三年级人数:200×16%=200×0.16=32(人)四年级人数:200×10%=200×0.1=20(人)32:20=8:5答:三年级和四年级参加活动人数的比是8:5。(3)从这幅统计图中不能得出“五年级参加活动人数最多”的结论,理由是:一二年级参加活动的人数共占全校参加活动总人数的32%,有可能其中一个年级占的百分率比五年级多。故答案为:200;8:5。分析变式01(1)把总人数看作单位“1”,根据减法的意义,用减法。(2)先求出参加科技类的学生和参加体育类的学生共占总人数的百分之几,然后根据求一个数的百分之几是多少,用乘法解答。建设路小学这个学期的课后服务形式多样,如图是六年级120名学生参加课后服务活动的情况统计图。(1)参加书法类的学生占全部学生的 %。(2)参加科技类的学生和参加体育类的学生一共有 人。点评解答此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。解:(1)1﹣25%﹣30%﹣30%=15%答:参加书法类的学生占全部学生的15%。(2)120×(25%+30%)=120×55%=66(人)答:参加科技类的学生和参加体育类的学生一共有66人。故答案为:15;66。分析变式02(1)把调查的总人数看作单位“1”,参与调查活动中经历虚假中奖的有50人,占调查总人数的25%,根据已知一个数的百分之几是多少,求这个数,用除法求出调查的总人数,再根据求一个数的百分之几是多少,用乘法解答。(2)把经历电话诈骗的人数看作单位“1”,根据求一个数比另一个数少百分之几,用除法解答。一些不法分子的诈骗手段越来越多样,为了防止人们上当受骗,网通公司开展了“经历最多的诈骗方式”调查活动,参与调查活动中经历虚假中奖的有50人。经过整理分析后,绘制成了如图的扇形统计图。(1)参与调查的一共有 人,经历电话诈骗的有 人,经历QQ诈骗的有 人。(2)经历QQ诈骗的人数比经历电话诈骗的人数少百分之几?点评解答此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。解:(1)50÷25%=50÷0.25=200(人)200×20%=40(人)200×15%=30(人)答:参与调查的一共有200人,经历电话诈骗的有40人,经历QQ诈骗的有30人。(2)(40﹣30)÷40=10÷40=0.25=25%答:经历QQ诈骗的人数比经历电话诈骗的人数少25%。故答案为:200,40,30。分析变式03根据百分数除法的意义,用喜欢排球运动的人数除以所占的百分率就是该年级总人数;再根据百分数乘法的意义,用这个年级总人数乘喜欢乒乓球人数所占的百分率就是喜欢乒乓球运动的人数。为了组织球类比赛,学校调查了六年级学生最喜欢的球类运动,统计如图。如果喜欢排球运动的有30人,喜欢乒乓球运动的一共有多少人?点评解答此题是考查如何从扇形统计图中获取信息,并根据所获取的信息解决实际问题。解:30÷15%×50%=200×50%=100(人)答:喜欢乒乓球运动的有100人。分析典例02因为折线统计图能清楚地反映事物的变化情况,所以根据数据,在图中制作出折线统计图即可。下面是某棵柳树6年生长情况的统计根据以上数据,选择合适的统计图表示树的生长趋势。点评解答解答此题的关键利用表中已知的信息,结合给出的条件,完成统计图。解:如图:分析变式01条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。校运会时请根据需要选择合适的统计图类型。(将正确答案的序号填在横线上)①游园活动时,比较各班获奖人数的多少时,可以选择 统计图。②要想看看五年级近几届50米跑成绩的上升和下降情况,应绘制 统计图。③想要了解各班获奖人数与整个年级的百分比,常选用 统计图。A.折线 B.条形 C.扇形点评解答此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。解:①游园活动时,比较各班获奖人数的多少时,可以选择统计图。②要想看看五年级近几届50米跑成绩的上升和下降情况,应绘制折线统计图。③想要了解各班获奖人数与整个年级的百分比,常选用扇形统计图。故答案为:B、A、C。分析变式02(1)根据折线统计图的特点:不但可以表示出数量的多少,而且能够清楚的表示出数量增减变化的情况;进而得出结论;(2)①先求出四个季度的总产值,进而根据“总数÷数量=平均数”求出平均每个季度产值;②先求出下半年的总产值,进而根据“下半年的总产值÷月份=平均每个月的产值”进行解答即可;③先求出第二季度比第一季度增产多少万元,进而根据求一个数是另一个数的几分之几,用除法进行解答即可.某企业2006年的产值如下:(1)既要直观反映出这个企业每个季度的产值是多少,又要反映出产值的增长变化情况应绘制 统计图.(2)平均每个季度产值 万元,下半年平均每个月产值 万元,第二季度比第一季度增产 %.点评解答解答此题的关键:(1)根据平均数、数量和总数之间的关系进行解答;(2)根据求一个数比另一个数多几分之几,用“(大数﹣小数)÷单位“1”的量”进行解答.解:(1)既要直观反映出这个企业每个季度的产值是多少,又要反映出产值的增长变化情况应绘制折线统计图;(2)(610+700+810+840)÷4,=2960÷4,=740(万元);(810+840)÷(3+3),=1650÷6,=275(万元);(700﹣610)÷610,=90÷610,≈14.8%;故答案为:折线,740,275,14.8.分析变式03条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可.我国从第23届奥运会开始获得奖牌.下面是第26届~29届奥运会我国获奖牌情况统计图表.(1)从哪幅图能明显地看出我国在第26届~29届奥运会获奖金牌的变化情况?(2)从哪幅图能更明显地看出第29届奥运会我国获得和金牌数?(3)从哪幅图能看出第29届奥运会我国奖牌的分布情况?点评解答此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答.解:根据统计图的特点可知:(1)从图三折线统计图中能明显地看出我国在第26届~29届奥运会获奖金牌的变化情况;(2)从图一条形统计图中能更明显地看出第29届奥运会我国获得和金牌数;(3)从图二扇形统计图中能看出第29届奥运会我国奖牌的分布情况.分析典例03(1)根据表格中正字的多少,将结果填入下面的表格中即可;(2)根据表格可得种植的哪种树最多,哪种树最少;(3)将所有的棵树相加,即可求出一共种植了多少棵树;用杨树的棵树减去杉树的棵树,即可求出种植的杉树比杨树少多少棵。1.把记录的结果填入下表。2.春风小学种植的 树最多, 树最少。3.春风小学一共种植了 棵树,种植的杉树比杨树少 棵。点评解答此题考查统计表的应用。进一步考查学生识表解决问题的能力。解:1、2、春风小学种植的杨树最多,槐树最少;3、一共种植:20+16+15+11=62(棵)杉树比杨树少:20﹣15=5(棵)答:春风小学一共种植了62棵树,种植的杉树比杨树少5棵。故答案为:杨,槐;62,5。分析变式01已知5月份有31天,用31﹣3﹣8﹣4即可求出晴天的天数,然后根据求一个数占另一个数的几分之几,用一个数除以另一个数,则用(31﹣3﹣8﹣4)÷31即可求出晴天的天数占全月总天数的几分之几。某城市5月分天气情况如下表所示。请你先填表,再回答问题:晴天的天数占全月总天数的几分之几?点评解答本题主要考查了统计表的整理和分析知识,求一个数占另一个数的几分之几,用除法计算。解:31﹣3﹣8﹣4=16(天)16÷31=答:晴天的天数占全月总天数的 。分析变式02(1)根据第一次跳的+第二次跳的=一共跳的,一共跳的﹣第一次跳的=第二次跳的,计算并填写在表内;(2)把三个人一共跳的个数比较,找出跳的最多的一个。跳绳比赛。(1)把表填完整。(2) 两次加起来最多。点评解答本题考查统计表的应用。解题关键是正确读取表中信息,并能利用已知信息解决问题。解:(1)30+40=70(下)68﹣20=48(下)52+30=82(下)(2)82>70>48答:小玲两次加起来最多。故答案为:(1)70;48;82;(2)小玲。分析变式02由题意可知,图中虚线所指的位置是小强平均每次颠球的个数,即平均颠球10个,四次即10×4=40(个),分别减去第一次,第二次,第三次即可得到第四次颠球个数,根据条形统计图的绘制的方法,按照统计表中的实际完成统计图即可。如图是小强四次颠球个数情况统计图,图中虚线所指的位置是小强平均每次颠球的个数,算一算,小强第四次颠球多少个?并在图中把它补充完整。点评解答此题考查的目的是理解掌握条形统计图绘制方法及应用,并且能够根据统计图提供的信息,解决有关的实际问题。解:10×4﹣(6+8+14)=40﹣28=12(个)课程结束
北师大数学六年级上册 第五单元《数据处理》单元热点难点知识网络扇形统计图是用整个圆的面积表示总数量,用圆内各扇形的面积表示各部分数量占总数量的百分比。知识梳理要正确选择合适的统计图进行统计,首先要掌握三种统计图的不同特点,再根据不同的特点结合实际情况在反复实践中加强对比,这样才能选择合适的统计图。在分组整理数据时,要根据实际情况来确定每一段的数量,以便清楚地表达信息。在同等情况下,折线越陡,数量变化越大,反之,数量变化越小。分析典例01(1)由题意可知,把全校参加活动人数看作单位“1”,根据六年级参加活动的36人是全校参加活动总人数的18%,可用“36÷18%求出全校参加活动的总人数;(2)分别用全参加活动的总人数乘三年级和四年级对应的百分率,就可求出三年级的四年级参加活动的人数,再写成比的形式并化简;(3)不能,因为一二年级参加活动的人数共占全校参加活动总人数的32%,有可能其中一个年级占的百分率比五年级多。学校开展劳动教育实践活动。数学统计小组对各年级同学参加活动人数情况做了调查,并绘制了扇形统计图。请你根据图中提供的信息,解答下列问题。(1)六年级有36人参加活动,全校共有 人参加活动。(2)三年级和四年级参加活动人数的比是 : 。(3)从这幅统计图中能否得出“五年级参加活动人数最多”的结论?请说明理由。精讲精练点评解答解决本题关键是从图中读出数据,找出单位“1”,再根据基本的数量关系求解。解:(1)36÷18%=36÷0.18=200(人)答:全校有200人参加活动。(2)三年级人数:200×16%=200×0.16=32(人)四年级人数:200×10%=200×0.1=20(人)32:20=8:5答:三年级和四年级参加活动人数的比是8:5。(3)从这幅统计图中不能得出“五年级参加活动人数最多”的结论,理由是:一二年级参加活动的人数共占全校参加活动总人数的32%,有可能其中一个年级占的百分率比五年级多。故答案为:200;8:5。分析变式01(1)把总人数看作单位“1”,根据减法的意义,用减法。(2)先求出参加科技类的学生和参加体育类的学生共占总人数的百分之几,然后根据求一个数的百分之几是多少,用乘法解答。建设路小学这个学期的课后服务形式多样,如图是六年级120名学生参加课后服务活动的情况统计图。(1)参加书法类的学生占全部学生的 %。(2)参加科技类的学生和参加体育类的学生一共有 人。点评解答此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。解:(1)1﹣25%﹣30%﹣30%=15%答:参加书法类的学生占全部学生的15%。(2)120×(25%+30%)=120×55%=66(人)答:参加科技类的学生和参加体育类的学生一共有66人。故答案为:15;66。分析变式02(1)把调查的总人数看作单位“1”,参与调查活动中经历虚假中奖的有50人,占调查总人数的25%,根据已知一个数的百分之几是多少,求这个数,用除法求出调查的总人数,再根据求一个数的百分之几是多少,用乘法解答。(2)把经历电话诈骗的人数看作单位“1”,根据求一个数比另一个数少百分之几,用除法解答。一些不法分子的诈骗手段越来越多样,为了防止人们上当受骗,网通公司开展了“经历最多的诈骗方式”调查活动,参与调查活动中经历虚假中奖的有50人。经过整理分析后,绘制成了如图的扇形统计图。(1)参与调查的一共有 人,经历电话诈骗的有 人,经历QQ诈骗的有 人。(2)经历QQ诈骗的人数比经历电话诈骗的人数少百分之几?点评解答此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。解:(1)50÷25%=50÷0.25=200(人)200×20%=40(人)200×15%=30(人)答:参与调查的一共有200人,经历电话诈骗的有40人,经历QQ诈骗的有30人。(2)(40﹣30)÷40=10÷40=0.25=25%答:经历QQ诈骗的人数比经历电话诈骗的人数少25%。故答案为:200,40,30。分析变式03根据百分数除法的意义,用喜欢排球运动的人数除以所占的百分率就是该年级总人数;再根据百分数乘法的意义,用这个年级总人数乘喜欢乒乓球人数所占的百分率就是喜欢乒乓球运动的人数。为了组织球类比赛,学校调查了六年级学生最喜欢的球类运动,统计如图。如果喜欢排球运动的有30人,喜欢乒乓球运动的一共有多少人?点评解答此题是考查如何从扇形统计图中获取信息,并根据所获取的信息解决实际问题。解:30÷15%×50%=200×50%=100(人)答:喜欢乒乓球运动的有100人。分析典例02因为折线统计图能清楚地反映事物的变化情况,所以根据数据,在图中制作出折线统计图即可。下面是某棵柳树6年生长情况的统计根据以上数据,选择合适的统计图表示树的生长趋势。点评解答解答此题的关键利用表中已知的信息,结合给出的条件,完成统计图。解:如图:分析变式01条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。校运会时请根据需要选择合适的统计图类型。(将正确答案的序号填在横线上)①游园活动时,比较各班获奖人数的多少时,可以选择 统计图。②要想看看五年级近几届50米跑成绩的上升和下降情况,应绘制 统计图。③想要了解各班获奖人数与整个年级的百分比,常选用 统计图。A.折线 B.条形 C.扇形点评解答此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。解:①游园活动时,比较各班获奖人数的多少时,可以选择统计图。②要想看看五年级近几届50米跑成绩的上升和下降情况,应绘制折线统计图。③想要了解各班获奖人数与整个年级的百分比,常选用扇形统计图。故答案为:B、A、C。分析变式02(1)根据折线统计图的特点:不但可以表示出数量的多少,而且能够清楚的表示出数量增减变化的情况;进而得出结论;(2)①先求出四个季度的总产值,进而根据“总数÷数量=平均数”求出平均每个季度产值;②先求出下半年的总产值,进而根据“下半年的总产值÷月份=平均每个月的产值”进行解答即可;③先求出第二季度比第一季度增产多少万元,进而根据求一个数是另一个数的几分之几,用除法进行解答即可.某企业2006年的产值如下:(1)既要直观反映出这个企业每个季度的产值是多少,又要反映出产值的增长变化情况应绘制 统计图.(2)平均每个季度产值 万元,下半年平均每个月产值 万元,第二季度比第一季度增产 %.点评解答解答此题的关键:(1)根据平均数、数量和总数之间的关系进行解答;(2)根据求一个数比另一个数多几分之几,用“(大数﹣小数)÷单位“1”的量”进行解答.解:(1)既要直观反映出这个企业每个季度的产值是多少,又要反映出产值的增长变化情况应绘制折线统计图;(2)(610+700+810+840)÷4,=2960÷4,=740(万元);(810+840)÷(3+3),=1650÷6,=275(万元);(700﹣610)÷610,=90÷610,≈14.8%;故答案为:折线,740,275,14.8.分析变式03条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可.我国从第23届奥运会开始获得奖牌.下面是第26届~29届奥运会我国获奖牌情况统计图表.(1)从哪幅图能明显地看出我国在第26届~29届奥运会获奖金牌的变化情况?(2)从哪幅图能更明显地看出第29届奥运会我国获得和金牌数?(3)从哪幅图能看出第29届奥运会我国奖牌的分布情况?点评解答此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答.解:根据统计图的特点可知:(1)从图三折线统计图中能明显地看出我国在第26届~29届奥运会获奖金牌的变化情况;(2)从图一条形统计图中能更明显地看出第29届奥运会我国获得和金牌数;(3)从图二扇形统计图中能看出第29届奥运会我国奖牌的分布情况.分析典例03(1)根据表格中正字的多少,将结果填入下面的表格中即可;(2)根据表格可得种植的哪种树最多,哪种树最少;(3)将所有的棵树相加,即可求出一共种植了多少棵树;用杨树的棵树减去杉树的棵树,即可求出种植的杉树比杨树少多少棵。1.把记录的结果填入下表。2.春风小学种植的 树最多, 树最少。3.春风小学一共种植了 棵树,种植的杉树比杨树少 棵。点评解答此题考查统计表的应用。进一步考查学生识表解决问题的能力。解:1、2、春风小学种植的杨树最多,槐树最少;3、一共种植:20+16+15+11=62(棵)杉树比杨树少:20﹣15=5(棵)答:春风小学一共种植了62棵树,种植的杉树比杨树少5棵。故答案为:杨,槐;62,5。分析变式01已知5月份有31天,用31﹣3﹣8﹣4即可求出晴天的天数,然后根据求一个数占另一个数的几分之几,用一个数除以另一个数,则用(31﹣3﹣8﹣4)÷31即可求出晴天的天数占全月总天数的几分之几。某城市5月分天气情况如下表所示。请你先填表,再回答问题:晴天的天数占全月总天数的几分之几?点评解答本题主要考查了统计表的整理和分析知识,求一个数占另一个数的几分之几,用除法计算。解:31﹣3﹣8﹣4=16(天)16÷31=答:晴天的天数占全月总天数的 。分析变式02(1)根据第一次跳的+第二次跳的=一共跳的,一共跳的﹣第一次跳的=第二次跳的,计算并填写在表内;(2)把三个人一共跳的个数比较,找出跳的最多的一个。跳绳比赛。(1)把表填完整。(2) 两次加起来最多。点评解答本题考查统计表的应用。解题关键是正确读取表中信息,并能利用已知信息解决问题。解:(1)30+40=70(下)68﹣20=48(下)52+30=82(下)(2)82>70>48答:小玲两次加起来最多。故答案为:(1)70;48;82;(2)小玲。分析变式02由题意可知,图中虚线所指的位置是小强平均每次颠球的个数,即平均颠球10个,四次即10×4=40(个),分别减去第一次,第二次,第三次即可得到第四次颠球个数,根据条形统计图的绘制的方法,按照统计表中的实际完成统计图即可。如图是小强四次颠球个数情况统计图,图中虚线所指的位置是小强平均每次颠球的个数,算一算,小强第四次颠球多少个?并在图中把它补充完整。点评解答此题考查的目的是理解掌握条形统计图绘制方法及应用,并且能够根据统计图提供的信息,解决有关的实际问题。解:10×4﹣(6+8+14)=40﹣28=12(个)课程结束

相关资料
更多









