2023-2024学年河南省开封市禹王台区铁路中学八年级（下）期末数学试卷（含答案）

这是一份2023-2024学年河南省开封市禹王台区铁路中学八年级（下）期末数学试卷（含答案），共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题：本题共10小题，每小题3分，共30分。在每小题给出的选项中，只有一项是符合题目要求的。
1.计算3a2a−1+a+11−2a的结果是( )
A. 1B. −1C. 2a+12a−1D. 4a+12a−1
2.如图，已知点A1(1,1)，点A1先向上平移1个单位长度，再向右平移2个单位长度，得到点A2；点A2先向上平移2个单位长度，再向右平移4个单位长度，得到点A3，点A3先向上平移4个单位长度，再向右平移8个单位长度，得到点A4……按这个规律平移得到点An，则点An的纵坐标为( )
A. 2nB. 2n−1C. 2n−1D. 2n+1
3.平行四边形OABC的边OA在x轴上，顶点C在反比例函数y=kx的图象上，BC与y轴相交于点D，且D为BC的中点，若平行四边形OABC的面积为8，则k的值为( )
A. −2 B. 2
C. −4 D. 4
4.如图，在平行四边形ABCD中，∠DBC=45°，DE⊥BC于E，BF⊥CD于F，DE，BF相交于H，BF与AD的延长线相交于点G，下面给出四个结论：①BD= 2BE；②∠A=∠BHE；③AB=BH；④△BCF≌△DCE，其中正确的结论有( )
A. 4个
B. 3个
C. 2个
D. 1个
5.在平面直角坐标系中，已知点A(0,0)、B(5,0)、C(2,3)，以A、B、C三点为顶点画平行四边形，则第四个顶点D的坐标不可能是( )
A. (7,3) B. (−3,3)
C. (3,−3) D. (−2,−3)
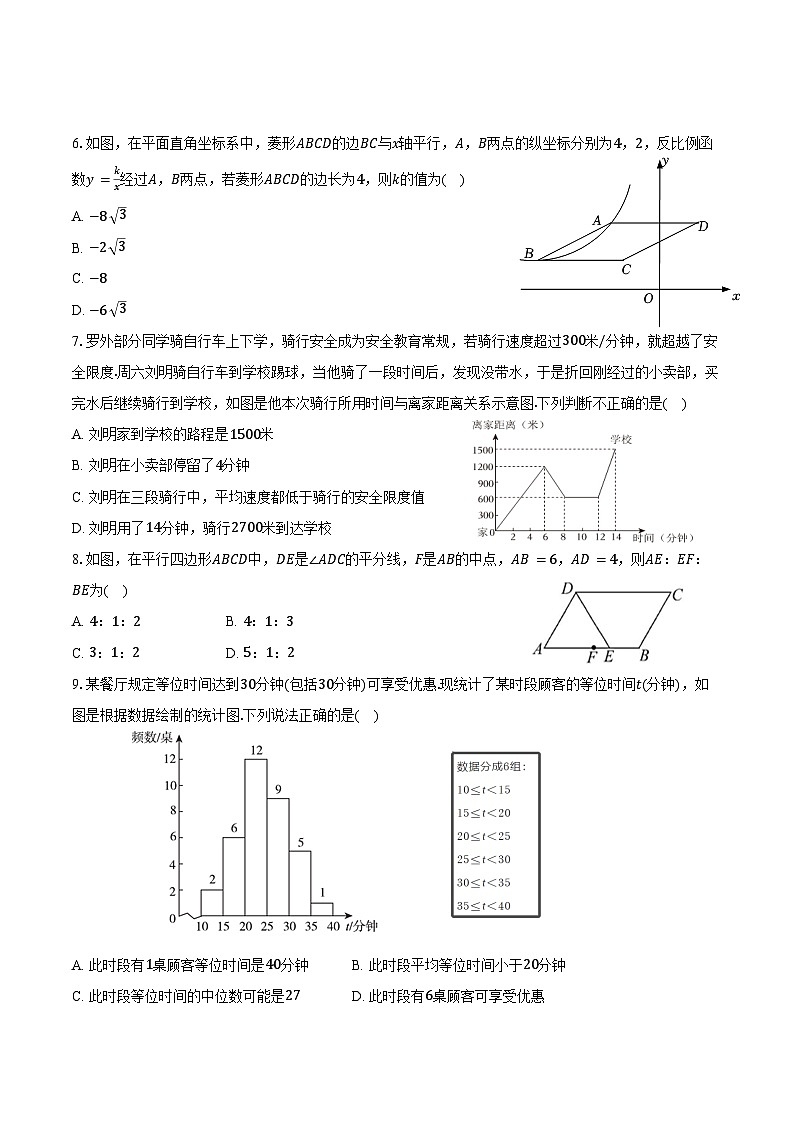
6.如图，在平面直角坐标系中，菱形ABCD的边BC与x轴平行，A，B两点的纵坐标分别为4，2，反比例函数y=kx经过A，B两点，若菱形ABCD的边长为4，则k的值为( )
A. −8 3
B. −2 3
C. −8
D. −6 3
7.罗外部分同学骑自行车上下学，骑行安全成为安全教育常规，若骑行速度超过300米/分钟，就超越了安全限度.周六刘明骑自行车到学校踢球，当他骑了一段时间后，发现没带水，于是折回刚经过的小卖部，买完水后继续骑行到学校，如图是他本次骑行所用时间与离家距离关系示意图.下列判断不正确的是( )
A. 刘明家到学校的路程是1500米
B. 刘明在小卖部停留了4分钟
C. 刘明在三段骑行中，平均速度都低于骑行的安全限度值
D. 刘明用了14分钟，骑行2700米到达学校
8.如图，在平行四边形ABCD中，DE是∠ADC的平分线，F是AB的中点，AB=6，AD=4，则AE：EF：BE为( )
A. 4：1：2B. 4：1：3
C. 3：1：2D. 5：1：2
9.某餐厅规定等位时间达到30分钟(包括30分钟)可享受优惠.现统计了某时段顾客的等位时间t(分钟)，如图是根据数据绘制的统计图.下列说法正确的是( )
A. 此时段有1桌顾客等位时间是40分钟B. 此时段平均等位时间小于20分钟
C. 此时段等位时间的中位数可能是27D. 此时段有6桌顾客可享受优惠
10.如图，平行四边形ABCD的对角线AC、BD相交于点O，AE平分∠BAD，分别交BC、BD于点E、P，连接OE，∠ADC=60°，AB=12BC=1，则下列结论中，不正确的是( )
A. ∠CAD=30°B. BD= 7C. OE=14ADD. S△AOE= 34
二、填空题：本题共5小题，每小题3分，共15分。
11.关于x的分式方程7xx−1−2m−1x−1=5无解，则m的值为______．
12.一艘轮船在静水中的最大航速为30km/ℎ，它以最大航速沿江顺流航行120km所用时间，与以最大航速逆流航行60km所用时间相同，则江水的流速为______km/ℎ．
13.在测量液体密度的实验中，根据测得的液体和烧杯的总质量m(g)与液体的体积V(cm3)，绘制了如图所示的函数图象(图中为一线段)，则当V=80cm3时，m为______g.
14.如图，在△ABC中，AB=AC，∠BCA=60°，∠BAE=150°，DC⊥AB且DC=AE，若DC=kAG(k为常数且k> 3)，设AG=x，DE=y，则y关于x的函数解析式为______(用含有k的代数式表示)．
15.如图，在平行四边形ABCD中，AB=6cm，AD=10cm，点P在AD边上以每秒1cm的速度从点A向点D运动，点Q在BC边上以每秒4cm的速度从点C出发，在CB间往返运动，两个点同时出发，当点P到达点D时停止运动，同时点Q也停止运动.设运动时间为t s，开始运动以后，当t为______时，以P，D，Q，B为顶点的四边形是平行四边形．
三、解答题：本题共8小题，共75分。解答应写出文字说明，证明过程或演算步骤。
16.(本小题8分)
解方程：
(1)5x−2+1=x−12−x；
(2)3x−3−4x2−9=0．
17.(本小题9分)
如图，在平行四边形ABCD中，AE⊥BD于E，CF⊥BD于F．
(1)求证：AE=CF．
(2)若BE=4，AB=5，求CF．
18.(本小题9分)
如图，在▱ABCD中，∠ABC的平分线交AD于点E，延长BE交CD的延长线于F．
(1)若∠F=28°，求∠A的度数；
(2)若AB=5，BC=8，CE⊥AD，求▱ABCD的面积．
19.(本小题9分)
如图，一次函数y=kx+b与反比例函数y=ax的图象在第一象限交于点A(4,3)，与y轴的负半轴交于点B，且OA=OB．
(1)求一次函数y=kx+b与反比例函数y=ax的表达式；
(2)已知点C在x轴上，且△ABC的面积是8，求此时点C的坐标；
(3)请直接写出不等式00，
∴AE=3．
∴CF=AE=3．
18.解：(1)∵四边形ABCD是平行四边形，
∴AD//BC，AD=BC，CD=AB，AB//CD，
∴∠AEB=∠CBF，∠ABE=∠F=28°，
∵∠ABC的平分线交AD于点E，
∴∠ABE=∠CBF，
∴∠AEB=∠ABE=28°，
∴AE=AB，∠A=180°−28°−28°=124°；
(2)∵AE=AB=5，AD=BC=8，CD=AB=5，
∴DE=AD−AE=3，
∵CE⊥AD，
∴CE= CD2−DE2= 52−32=4，
∴▱ABCD的面积=AD⋅CE=8×4=32．
19.解：(1)∵点A(4,3)在反比例函数y=ax的图象上，
∴a=4×3=12，
∴反比例函数解析式为y=12x；
∵∵OA= 42+32=5，OA=OB，点B在y轴负半轴上，
∴点B(0,−5)．
把点A(4,3)、B(0,−5)代入y=kx+b中，
得4k+b=3b=−5，解得：k=2b=−5，
∴一次函数的解析式为y=2x−5；
(2)设点C的坐标为(m,0)，令直线AB与x轴的交点为D，如图1所示．
令y=2x−5中y=0，则x=52，
∴D(52,0)，
∴S△ABC=12CD⋅(yA−yB)=12|m−52||×[3−(−5)]=8，
解得：m=12或m=92．
故当△ABC的面积是8时，点C的坐标为(12,0)或(92,0)；
(3)观察图象，由点A的坐标可知，不等式0