2023-2024学年江西省上饶市余干县瑞洪中学八年级（下）期末数学试卷（含详细答案解析）

这是一份2023-2024学年江西省上饶市余干县瑞洪中学八年级（下）期末数学试卷（含详细答案解析），共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.下列各式是二次根式的是( )
A. a2+1B. −7C. aD. 33
2.在学校举行的“阳光少年励志青春”演讲比赛中，5位评委给选手小明的评分分别为90，85，90，80，95，则这组数据的平均数是( )
A. 88B. 85C. 90D. 89
3.下列各组数据中的三个数作为三角形的边长，其中能构成直角三角形的是( )
A. 3， 4， 5B. 1， 2， 3C. 6，7，8D. 8，9，10
4.如图，在平行四边形ABCD中，∠ODA=90∘，AC=10cm，BD=6cm，则该平行四边形ABCD的周长为( )
A. 16cmB. 8+4 13cmC. 4+4 13cmD. 20cm
5.如图，正方形ABCD和正方形CEFG中，点D在CG上，BC=1，CE=3，H是AF的中点，那么CH的长是( )
A. 5B. 10C. 3 22D. 2
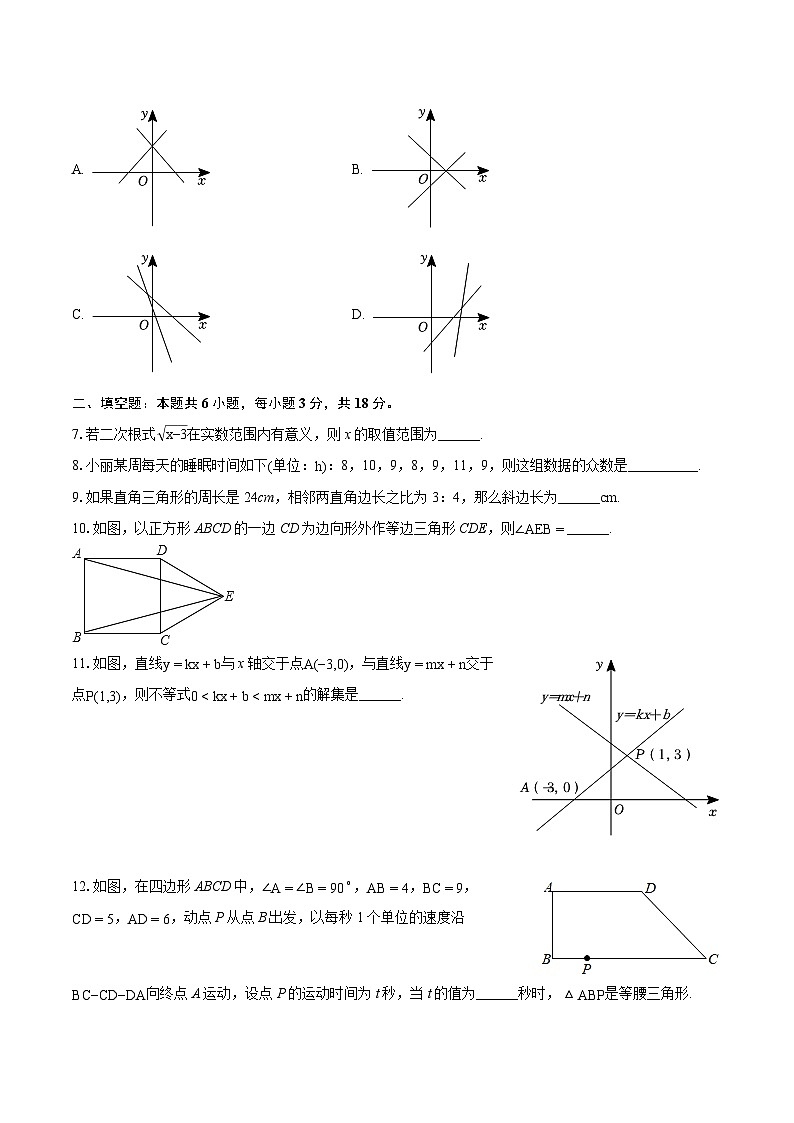
6.已知一次函数y=x+2的图象经过点P(a,b)，其中a≠0，b≠0，则关于x的一次函数y=ax+b和y=bx+a的图象可能是( )
A. B.
C. D.
二、填空题：本题共6小题，每小题3分，共18分。
7.若二次根式 x−3在实数范围内有意义，则x的取值范围为______.
8.小丽某周每天的睡眠时间如下(单位：h)：8，10，9，8，9，11，9，则这组数据的众数是__________.
9.如果直角三角形的周长是24cm，相邻两直角边长之比为3：4，那么斜边长为______cm.
10.如图，以正方形ABCD的一边CD为边向形外作等边三角形CDE，则∠AEB=______.
11.如图，直线y=kx+b与x轴交于点A(−3,0)，与直线y=mx+n交于点P(1,3)，则不等式012.如图，在四边形ABCD中，∠A=∠B=90∘，AB=4，BC=9，CD=5，AD=6，动点P从点B出发，以每秒1个单位的速度沿BC−CD−DA向终点A运动，设点P的运动时间为t秒，当t的值为______秒时，△ABP是等腰三角形.
三、解答题：本题共11小题，共84分。解答应写出文字说明，证明过程或演算步骤。
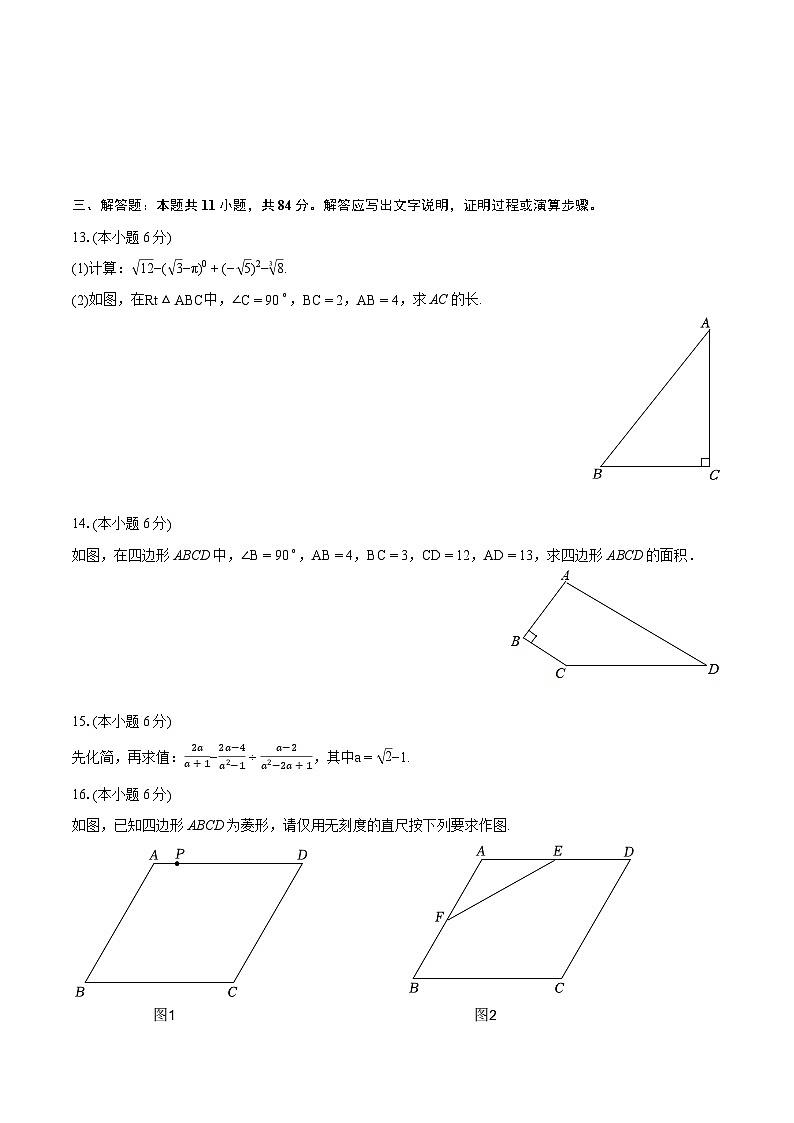
13.(本小题6分)
(1)计算： 12−( 3−π)0+(− 5)2−38.
(2)如图，在Rt△ABC中，∠C=90∘，BC=2，AB=4，求AC的长.
14.(本小题6分)
如图，在四边形ABCD中，∠B=90∘，AB=4，BC=3，CD=12，AD=13，求四边形ABCD的面积．
15.(本小题6分)
先化简，再求值：2aa+1−2a−4a2−1÷a−2a2−2a+1，其中a= 2−1.
16.(本小题6分)
如图，已知四边形ABCD为菱形，请仅用无刻度的直尺按下列要求作图.
(1)如图(1)，点P为AD上任意一点，作直线PQ将菱形分为面积相等的两部分；
(2)如图(2)，点E、F为AD、AB边中点，以EF为边作一个矩形.
17.(本小题6分)
在一次数学考试中，从某班随机抽取的10名学生得分如下：75，85，90，90，95，85，95，95，100，98.
(1)求这10个得分的众数、中位数和平均数；
(2)本次考试规定：达到96分及以上的为优秀.若该班共有40名学生，估计该班在此次考试中达到优秀的有多少名学生？
18.(本小题8分)
某公司招聘职员，对甲、乙两位候选人进行了面试和笔试，面试中包括形体和口才，笔试中包括专业水平和创新能力考察，他们的成绩(百分制)如下表：
(1)若公司根据经营性质和岗位要求认为：形体、口才、专业水平、创新能力按照4：6：5：5的比确定，请计算甲、乙两人各自的平均成绩，看看谁将被录取？
(2)若公司根据经营性质和岗位要求认为：面试成绩中形体占15%，口才占20%，笔试成绩中专业水平占40%，创新能力占25%，那么你认为该公司应该录取谁.
19.(本小题8分)
如图，已知平行四边形ABCD，∠ABC，∠BCD的平分线BE、CF分别交AD于E、F，BE、CF交于点G，点H为BC的中点，GH的延长线交GB的平行线CM于点M.
(1)试说明：∠BGC=90∘；
(2)连接BM，判断四边形GBMC的形状并说明理由.
20.(本小题8分)
如图，E、F、M、N分别是正方形ABCD四条边上的点，且AE=BF=CM=DN
(1)求证：四边形EFMN是正方形；
(2)若AB=7，AE=3，求四边形EFMN的周长．
21.(本小题9分)
如图，直线y=2x+4与x轴交于点A，与y轴交于点B，点C是OB的中点.
(1)求点C的坐标；
(2)在x轴上找一点D，使得S△ACD=S△ABC，求点D的坐标；
(3)点P在y轴上，且三角形AOB的面积是三角形AOP面积的2倍，直接写出点P的坐标.
22.(本小题9分)
【阅读理解】阅读下列材料，然后解答下列问题.
像( 5+2)( 5−2)=1， a⋅ a=a(a≥0)，( b+1)( b−1)=b−1(b≥0)，两个含有二次根式的代数式相乘，积不含有二次根式，我们称这两个代数式互为有理化因式.例如： 5与 5， 2+1与 2−1，2 3+3 5与2 3−3 5等都是互为有理化因式.进行二次根式计算时，利用有理化因式，可以化去分母中的根号，请回答下列问题：
(1)化简：①2 2=________________；
(2)计算：12− 3−1 3− 2；
(3)计算：(1 2+1+1 3+ 2+1 4+ 3+⋯+1 2023+ 2022)( 2023+1).
23.(本小题12分)
阅读材料：一般地，设平面上任意两点A(x1,y1)和B(x2,y2)可以用|AB|表示A、B两点之间的距离，那么该如何计算|AB|呢？作AA′⊥x轴、作BB′⊥x轴，垂足分别是点A′、B′；作AA′′⊥y轴，垂足为点A′′、作BB′′⊥y轴，垂足为点B′′，且与AA′交于点C，则四边形BB′A′C、ACB′′A′′是矩形.
∵|BC|=|x2−x1|，|AC|=|y2−y1|，
∴|AB|2=|AC|2+|BC|2=(x2−x1)2+(y2−y1)2.
∴|AB|= (x2−x1)2+(y2−y1)2.
这就是平面直角坐标系中两点之间的距离公式.
如：点A(1,4)和点B(5,2)之间的距离|AB|= (5−1)2+(2−4)2= 20=2 5.
(1)请运用公式计算点M(4,2)和点N(2,−1)之间的距离；
(2)在(1)的条件下，点O为原点，求△MNO的周长；
(3)平面直角坐标系中的两点E(1,3)、F(4,1)，P为x轴上任一点，当PE+PF值最小时，用尺规作出点P，并求出PE+PF的最小值.
答案和解析
1.【答案】A
【解析】解：A、a2+1≥1，则 a2+1是二次根式，故此选项符合题意；
B、 −7无意义，故此选项不符合题意；
C、当a<0时， a无意义，故此选项不符合题意；
D、33属于三次根式，故此选项不符合题意；
故选：A.
根据二次根式的定义逐个判断即可．
本题考查了二次根式的定义，能熟记二次根式的定义的内容是解此题的关键，注意：式子 a(a≥0)叫做二次根式．
2.【答案】A
【解析】解：90+85+90+80+955=4405=88.
故选：A.
在一组数据中，所有数据之和再除以数据的个数就是平均数；结合题中所给的数据，运用平均数的定义即可求解．
本题侧重考查平均数的题目，掌握平均数的求法是解题的关键．
3.【答案】B
【解析】解：对于选项A，
∵( 3)2+( 4)2=7，( 5)2=5，
∴( 3)2+( 4)2≠( 5)2，
∴选项A中的三个数作为三角形的边长，不能构成直角三角形，
故选项A不符合题意；
对于选项B，
∵12+( 2)2=3，( 3)2=3，
∴12+( 2)2=( 3)2，
∴选项B中的三个数作为三角形的边长，能构成直角三角形，
故选项B符合题意；
对于选项C，
∵62+72=85，82=64，
∴62+72≠82，
∴选项C中的三个数作为三角形的边长，不能构成直角三角形，
故选项C不符合题意；
对于选项D，
∵82+92=145，102=100，
∴82+92≠102，
∴选项D中的三个数作为三角形的边长，不能构成直角三角形，
故选项D不符合题意，
故选：B.
对于选项A，根据( 3)2+( 4)2≠( 5)2，再依据勾股定理逆定理即可对该选项进行判断；
对于选项B，根据12+( 2)2=( 3)2，再依据勾股定理逆定理即可对该选项进行判断；
对于选项C，根据62+72≠82，再依据勾股定理逆定理即可对该选项进行判断；
对于选项D，根据82+92≠102，再依据勾股定理逆定理即可对该选项进行判断；
综上所述即可得出答案．
此题主要考查了勾股定理的逆定理，熟练掌握勾股定理的逆定理是解决问题的关键．
4.【答案】B
【解析】解：∵四边形ABCD是平行四边形，
∴OA=12AC=5，OD=12BD=3，
∵∠ODA=90∘，
∴AD= OA2−OD2
= 52−32=4，
∴AB= AD2+BD2
= 42+62=2 13，
∴C▱ABCD=2(AD+AB)
=2(4+2 13)
=(8+4 13)cm，
故选：B.
由勾股定理可求AD=4，AB=2 13，即可求解．
本题考查了平行四边形的性质，勾股定理，掌握性质及定理是解题的关键．
5.【答案】A
【解析】【分析】
本题考查了正方形的性质：正方形的四条边都相等，四个角都是直角；正方形的两条对角线相等，互相垂直平分，并且每条对角线平分一组对角；正方形具有平行四边形、矩形、菱形的一切性质．两条对角线将正方形分成四个全等的等腰直角三角形．也考查了直角三角形斜边上的中线性质．
连接AC、CF，如图，根据正方形的性质得∠ACD=45∘，∠FCG=45∘，AC= 2，CF=3 2，则∠ACF=90∘，再利用勾股定理计算出AF=2 5，然后根据直角三角形斜边上的中线求CH的长．
【解答】解：连接AC、CF，如图，
∵四边形ABCD和四边形CEFG都是正方形，
∴∠ACD=45∘，∠FCG=45∘，AC= 2BC= 2，CF= 2CE=3 2，
∴∠ACF=45∘+45∘=90∘，
在Rt△ACF中，AF= ( 2)2+(3 2)2=2 5，
∵H是AF的中点，
∴CH=12AF= 5.
故选A.
6.【答案】B
【解析】解：∵一次函数y=x+2的图象经过点P(a,b)，
∴b=a+2，
∴一次函数y=ax+b=ax+a+2，即y=a(x+1)+2，
∴对于任意实数a，恒有当x=−1时，y=2，
∴一次函数y=ax+b的图象经过定点(−1,2)；
∵b=a+2，
∴a=b−2，
∴一次函数y=bx+a=bx+b−2，即y=b(x+1)−2，
∴对于任意实数，恒有当x=−1时，y=−2，
∴一次函数y=bx+a的图象经过定点(−1,−2).
故选B.
利用一次函数图象上点的坐标特征，可得出b=a+2，将其代入y=ax+b中变形后，可得出y=a(x+1)+2，进而可得出一次函数y=ax+b的图象经过定点(−1,2)；由b=a+2，可得出a=b−2，将其代入y=bx+a中变形后，可得出y=b(x+1)−2，进而可得出一次函数y=bx+a的图象经过定点(−1,−2).再对照四个选项中的函数图象，即可得出结论．
本题考查了一次函数图象上点的坐标特征以及一次函数的图象，利用一次函数图象上点的坐标特征，找出关于x的一次函数y=ax+b和y=bx+a的图象经过的定点坐标是解题的关键．
7.【答案】x≥3
【解析】解：∵二次根式 x−3在实数范围内有意义，
∴x−3≥0，解得x≥3.
故答案为：x≥3.
先根据二次根式有意义的条件列出关于x的不等式，求出x的取值范围即可．
本题考查了二次根式有意义的条件，掌握二次根式的被开方数大于等于0是关键．
8.【答案】9
【解析】解：在这一组数据中9是出现次数最多的，故众数是9.
故答案为：9.
众数是一组数据中出现次数最多的数，根据定义就可以求解．
本题考查众数的意义，解题的关键是掌握众数是一组数据中出现次数最多的数．
9.【答案】10
【解析】解：直角三角形两直角边分别为3x(cm)，4x(cm)，
则斜边长为： (3x)2+(4x)2=5x(cm)，
∴直角三角形的周长3x+4x+5x=12x=24cm，
∴x=2，
∴斜边长为：5×2=10cm，
故答案为：10.
设直角三角形两直角边分别为3x(cm)，4x(cm)，再根据勾股定理得斜边长为 (3x)2+(4x)2=5x(cm)，结合周长列出方程，求出x的值即可．
本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
10.【答案】30∘
【解析】
解：∵四边形ABCD是正方形，
∴AD=CD=BC，∠ADC=∠BCD=90∘.
∵△DCE是等边三角形，
∴CD=DE=CE，∠CDE=∠DCE=60∘.
∴AD=ED，BC=CE，∠ADE=150∘，∠BCE=150∘.
∴∠AED=∠BEC=15∘，
∴∠AEB=60∘−15∘−15∘=30∘.
故答案为30∘.
根据条件可以求出△ADE和△BCE为等腰三角形，就可以求出∠AED=∠BEC=15∘，从而可以求出∠AEB的度数．
本题考查了正方形的性质的运用，等边三角形的性质的运用，等腰三角形的性质的运用，解答时求出∠AED和∠BEC的度数很关键．
11.【答案】−3【解析】解：根据图象可知，不等式0故答案为：−3根据图象即可确定不等式组的解集．
本题考查了一次函数与一元一次不等式的关系，熟练掌握一次函数图象是解题的关键．
12.【答案】4或15.5或20
【解析】解：①当点P在BC上时，如图1，AB=BP=4，
∴t=4÷1=4(秒)；
②当点P在CD上时，AP=BP，过P作PE⊥AB于P，
∴AE=BE，
∵∠DAB=∠ABC=∠AEP=90∘，
∴AD//EP//BC，
∴DP=PC=52，
∴t=4+9+52=15.5(秒)；
③当点P在AD上时，AB=AP=4，
∴PD=AD−AP=6−4=2，
∴t=4+9+5+2=20(秒)；
综上，t的值是4秒或15.5秒或20秒时，△ABP是等腰三角形．
故答案为：4或15.5或20.
分三种情况：①当点P在BC上时，如图1，AB=BP=4，②当点P在CD上时，AP=BP，③当点P在AD上时，AB=AP=4，根据点P的运动速度和路程可得结论．
本题主要考查了等腰三角形的性质和判定，分情况讨论是本题的关键，注意不要丢解．
13.【答案】解：(1)原式=2 3−1+5−2=2+2 3；
(2)在Rt△ABC中，∠C=90∘，BC=2，AB=4，
∴AC= AB2−BC2= 16−4=2 3.
【解析】(1)利用二次根式的化简，零次幂，立方根进行计算即可；
(2)利用勾股定理可求解．
本题考查了勾股定理，实数的运算，掌握勾股定理是解题的关键．
14.【答案】解：连接AC，
在Rt△ABC中，
AC2=AB2+BC2=32+42=25，
所以AC=5，
在△ACD中，因为AC2+CD2=52+122=169=132=AD2
所以AC2+CD2=AD2，
所以∠ACD=90∘，
故S四边形ABCD=S△ABC+S△ACD
=12×AB×BC+12×AC×CD
=12×3×4+12×5×12
=6+30
=36.

【解析】本题主要考查勾股定理和三角形的面积，解答本题的关键是通过连接AC把四边形化成两个三角形，分割法求面积即可得解.
15.【答案】解：2aa+1−2(a−2)(a−1)(a+1)×(a−1)2a−2
=2aa+1−2a−2a+1
=2a+1，
把a= 2−1代入2a+1= 2.
【解析】先根据分式混合运算的法则把原式进行化简，再把a的值代入进行计算即可．
本题考查的是分式的化简求值，在解答此类题目时要注意通分及约分的灵活应用．
16.【答案】解：(1)如图1，直线PQ为所求直线；
(2)如图2，四边形EFGH为所求图形；

【解析】(1)连接AC，BD交于点O，连接PO，并延长交BC于点Q，则直线PQ为所求直线；
(2)连接AC，BD交于点O，连接EO，并延长交BC于点G，连接FO，并延长CD于点H，则四边形EFGH是所求图形．
本题考查了作图-复杂作图，菱形的性质，三角形中位线定理，矩形的判定，灵活运用这些性质解决问题是解题的关键．
17.【答案】解：(1)被抽取的10名学生得分出现次数最多的是95分，共出现3次，因此众数是95分，
将这10名学生成绩从小到大排列后，处在中间位置的两个数的平均数为90+952=92.5(分)，因此中位数是92.5，
这10名学生成绩的平均数为75+85×2+90×2+95×3+98+10010=90.8(分)，
答：众数是95，中位数是92.5，平均数是90.8；
(2)40×210=8(人)，
答：该班40名学生在此次考试中达到优秀的大约有8人．
【解析】(1)根据中位数、众数、平均数的计算方法进行计算即可；
(2)求出样本中优秀学生所占的百分比，估计总体中优秀所占的百分比，由频率=频数总数进行计算即可．
本题考查众数，中位数，算术平均数以及样本估计总体，掌握众数，中位数，算术平均数的计算方法以及样本估计总体的方法是正确解答的关键．
18.【答案】解：(1)形体、口才、专业水平、创新能力按照4：6：5：5的比确定，
则甲的平均成绩为86×4+90×6+96×5+92×54+6+5+5=91.2.
乙的平均成绩为92×4+88×6+95×5+93×54+6+5+5=91.8.
乙的成绩比甲的高，所以应该录取乙．
(2)面试成绩中形体占15%，口才占20%，笔试成绩中专业水平占40%，创新能力占25%，
则甲的平均成绩为86×15%+90×20%+96×40%+92×25%=92.3.
乙的平均成绩为92×15%+88×20%+95×40%+93×25%=92.65.
甲的成绩比乙的低，所以应该录取乙．
【解析】(1)由形体、口才、专业水平、创新能力按照4：6：5：5的比确定，根据加权平均数的计算方法分别计算不同权的平均数，比较即可，
(2)由面试成绩中形体占15%，口才占20%，笔试成绩中专业水平占40%，创新能力占25%，根据加权平均数的计算方法分别计算不同权的平均数，比较即可，
本题考查的是加权平均数的求法．本题易出现的错误是求形体、口才、专业水平、创新能力成绩的平均数，对平均数的理解不正确．
19.【答案】解：(1)∵∠ABC+∠BCD=180∘，BE、CF平分∠ABC，∠BCD，
∴∠GBC+∠GCB=90∘，∴∠BGC=90∘；
(2)∵点H为BC的中点，∴BH=CH=GH，
∵GB//CM，∴∠BGH=∠CMH，
∵∠HBG=∠HGB，∴∠HCM=∠HMC，
∴MH=BH=CH=GH，
∴四边形GBMC为矩形．
【解析】(1)由平行四边形的两邻角互补，可得∠GBC+∠GCB=90∘，从而得出∠BGC=90∘；
(2)由直角三角形的性质得BH=CH=GH，再由GB//CM，得∠BGH=∠CMH，则MH=BH=CH=GH，则四边形GBMC为矩形．
本题考查了矩形的判定和平行四边形的性质．
20.【答案】(1)证明：∵AE=BF=CM=DN，
∴AN=DM=CF=BE.
∵∠A=∠B=∠C=∠D=90∘，
∴△AEN≌△DMN≌△CFM≌△BEF(SAS).
∴EF=EN=NM=MF，∠ENA=∠DMN.
∴四边形EFMN是菱形，
∵∠ENA=∠DMN，∠DMN+∠DNM=90∘，
∴∠ENA+∠DNM=90∘.
∴∠ENM=90∘.
∴四边形EFMN是正方形；
(2)解：∵AB=7，AE=3，
∴AN=BE=AB−AE=4，
∴EN= AE2+AN2=5，
∴正方形EFMN的周长=4×5=20.
【解析】(1)通过证明△AEN，△DNM，△MCF，△FBE全等，先得出四边形ENMF是菱形，再证明四边形EFMN中一个内角为90∘，从而得出四边形EFMN是正方形的结论；
(2)根据AB=7，AE=3，可得AN=BE=AB−AE=4，根据勾股定理可得EN=5，进而可以解决问题．
本题主要考查了正方形的性质和判定，全等三角形的判定和性质，熟练掌握正方形的判定和性质是解题的关键．
21.【答案】解：(1)由直线y=2x+4与y轴交于点B，
令x=0，得y=4，即B(0,4)，
∴OB=4，
∵点C是OB的中点．
∴BC=OC=2，即C(0,2).
(2)由直线y=2x+4与x轴交于点A，
令y=0，得x=−2，
∴OA=2，
∴S△ABC=12BC⋅OA=12×2×2=2，
设点D的坐标为(a,0)，则AD=|a−(−2)|=|a+2|，
∴S△ACD=12AD⋅OC=12|a+2|×2=|a+2|，
∵S△ABC=S△ACD，
∴|a+2|=2，解得：a=0或a=−4，
即点D的坐标为(0,0)或(−4,0).
(3)∵OA=2，OB=4，
∴S△AOB=12OA⋅OB=12×2×4=4，
设点P的坐标为(0,b)，则OP=|b|，
∴S△AOP=12OA⋅OP=|b|，
∵三角形AOB的面积是三角形AOP面积的2倍，
∴4=2|b|，解得：b=2或b=−2，
即点P的坐标为(0,2)或(0,−2).
【解析】(1)令x=0，得到点B的坐标，利用线段中点的定义即可求解；
(2)易求△ABC的面积，设点D的坐标为(a,0)，则AD=|a−(−2)|=|a+2|，于是可用含a的代数式表示出△ACD的面积，进而列出方程求解即可；
(3)易求△AOB的面积，设点P的坐标为(0,b)，则OP=|b|，于是可用含b的代数式表示出△AOP的面积，进而列出方程求解即可．
本题主要考查一次函数与坐标轴围成图形的面积，根据题意设出所求点的坐标，根据等量关系列出方程是解题关键．
22.【答案】解：(1)2 2=2 2 2× 2= 2；
(2)12− 3−1 3− 2
=2+ 3(2− 3)(2+ 3)− 3+ 2( 3− 2)( 3+ 2)
=2+ 3− 3− 2
=2− 2；
(3)(1 2+1+1 3+ 2+1 4+ 3+⋯+1 2023+ 2022)( 2023+1)
=( 2−1+ 3− 2+ 4− 3+...+ 2023− 2022)( 2023+1)
=( 2023−1)( 2023+1)
=2022.
【解析】(1)分子和分母都乘 2，再求出答案即可；
(2)先分母有理化，再根据二次根式的加减法法则进行计算即可；
(3)化简第一个括号内的式子，然后利用平方差公式计算即可．
本题考查了二次根式的混合运算，互为有理化因式的定义及分母有理化的方法，并考查了利用分母有理化进行计算及探究相关式子的规律，本题属于中档题．
23.【答案】解：(1)MN= (4−2)2+(2+1)2= 13；
(2)OM= 42+22=2 5，ON= 22+12= 5.
∴△OMN的周长= 13+3 5；
(3)如图，点P即为所求．
∵F，F′关于x轴对称，
∴F′(4,−1)，
∴PE+PF的最小值=EF′= (4−1)2+(3+1)2=5.
【解析】(1)利用两点间距离公式求解；
(2)求出OM，ON，可得结论；
(3)作点F关于x轴的对称点F′，连接EF′交x轴于点P，连接PF，点P即为所求，PE+PF的最大值就是线段EF′的长．
本题考查作图-复杂作图，两点间的距离，矩形的判定，轴对称最短问题等知识，解题的关键是理解题意，学会利用轴对称解决最短问题．
候选人
面试
笔试
形体
口才
专业水平
创新能力
甲
86
90
96
92
乙
92
88
95
93